Тяготение и тяжесть

Тяготение и тяжесть. Тяготением называется то взаимное притяжение, которое обнаруживается между всеми телами природы и подчиняется закону, открытому Ньютоном: два тела или две какие бы то ни было материальные частицы с массами m и m', находящиеся друг от друга на расстоянии r, весьма большом сравнительно с их размерами, действуют друг на друга притягательной силой f, направленной по линии, их соединяющей; величина этой силы выражается формулой:

f = Gmm'/r², (1)

причем G есть коэффициент пропорциональности, зависящий только от, тех единиц, в которых измеряются массы m и m', расстояние r и сила f. Этот коэффициент численно равен той силе, с которой тяготеют друг к другу две массы, равные единице и находящиеся на единице расстояния друг от друга; он называется гравитационной постоянной. Если измерять m и m'в граммах, r в сантиметрах, f в динах, то числовое значение G будет 6, 667·10-8 ¹⁾.  Если тяготеющие друг к другу тела имеют шарообразную форму и состоят из концентрических однородных слоев, то взаимодействие их (на всяких расстояниях) совершается так, как если бы масса каждого тела была сосредоточена в его центре.   В установлении закона всемирного тяготения сыграло весьма большую роль данное Ньютоном доказательство того факта, что тяжесть, или сила веса земных тел, с одной стороны, и сила, удерживающая луну на ее орбите, с другой стороны, суть частные виды одной и той же силы тяготения. Это доказательство состоит в следующем: тело, находящееся на земной поверхности (т. е. на расстоянии земного радиуса от центра земли), стремится падать с ускорением 9,8 м/с²; луна же, отстоящая от земли приблизительно на 60 земных радиусов, имеет, в своем круговом движении около земли, «центростремительное» ускорение, равное 0,0027 м/с². Отношение 0,0027:9,8 равняется отношению 12:60²; таким образом ускорения камня и луны, а следовательно, и пропорциональные этим ускорениям силы притяжения к земле, оказываются в обратном отношении с квадратами их расстояний от центра земли, как и следует по формуле (1).

¹⁾ В астрономии единицы длины, массы и времени принимаются: среднее расстояние от Солнца до Земли, масса Солнца и средние сутки; при этих единицах G = 295,91·10^-6; эта величина в астрономии обозначается k².

Определение ускорения силы тяжести. Мерой напряжения силы тяжести на земном шаре служит то ускорение g, с которым тела стремятся падать на землю (в пустоте). Точнейшим прибором для измерения этого ускорения служит маятник; наблюдают период колебания маятника и отсюда вычисляют g. Из наблюдений, подтверждаемых теорией, найдено, что сила тяжести на земле изменяется с высотой и с широтой. Если обозначим g_φ,0 ускорение тяжести под широтой g_φ,h на уровне моря, g — ускорение тяжести под той же широтой на высоте h метров над уровнем моря, то

g_φ,h = g_φ,0(1-0?0000003h).

Отсюда видно, что килограммовый груз при поднятии на 1 метр становится легче на 0,3 миллиграмма. По мере приближения от полюсов к экватору ускорение силы тяжести уменьшается вследствие двух причин: 1) вследствие вращения земли (получаемое при этом телами центростремительное ускорение вычитается из ускорения, соответствующего силе тяготения; остаток соответствует наблюдаемому ускорению); 2) вследствие того, что земля имеет форму не шара, но — точнее — эллипсоида, сплющенного у полюсов. Результат обоих влияний передается формулой:

g_φ,0 = g_0,0 (1+sin²φ/190)  (2)

причем ускорение тяжести на экваторе g_0,0 = 9,780 м,с²

Для полюса формула (2) дает  g9_0,0 = 9,832. Таким образом, мы видим, что вес тела на полюсе приблизительно на ½ % больше, чем вес того же тела на экваторе. В следующей таблице указаны значения g для некоторых пунктов в пределах России (м/с²):

Петроград   9,819

Москва 9,816  

Одесса 9,807  

Ташкент  9,801  

Сравнение наблюдаемых значений g с «нормальными» значениями, вычисляемыми на основании известных теоретических предположений относительно формы земли, показывает, что в различных пунктах земли имеются более или менее заметные уклонения от нормального распределения величины (аномалии). Так, над континентальными горными массивами наблюдаемое g оказывается обыкновенно слишком малым, между тем в береговом поясе и на неглубоком море, близ берегов, а также на островах среди глубокого моря g бывает больше нормальной величины. Бывают также чисто местные аномалии, обусловливаемые, по-видимому, большими залежами пород, более тяжелых или более легких, чем остальная земная кора, или же наличностью подземных пустот.  Аномалиям подлежит не только величина, но и направление силы тяжести: так, отвесная линия испытывает уклонение в сторону больших гор (рис. 1) и вообще больших масс. Это уклонение можно констатировать и измерить, определяя координаты одной и той же звезды из двух пунктов, находящихся по разные стороны горы. У подошвы Кавказского хребта, во Владикавказе, такое уклонение достигает  35”,8; вблизи Хеопсовой пирамиды также заметно уклонение подобного рода. Особенности геологического строения местности (присутствие более плотных пород, подземные пустоты) оказывают свое влияние на направление отвесной линии. Из аномалий, относящихся сюда, замечательна московская: отвес в самой Москве отклонен на 10”,6 к северу.   

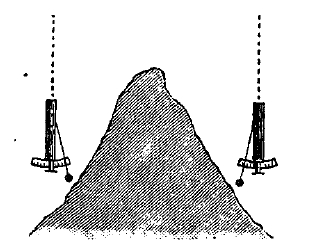
Рис. 1.

Определение гравитационной постоянной G имеет весьма важное значение, между прочим, в следующих отношениях: 1) зная G, g и размеры земли, можем вычислить массу земли и среднюю плотность ее; 2) зная массу земли, можно определить массу других планет и массу солнца.   Для определения G существует ряд способов; из них упомянем некоторые, наиболее известные.

1) Способ отклонения отвесной линии действием гор. В этом способе нужно по размерам горы и по плотности составляющих ее горных пород определять, в каком отношении находится притяжение, оказываемое ею на уровень, которым определяется отвесная линия, к притяжению, которое производит земля на тот же уровень. Но такое определение возможно лишь с малой степенью точности.

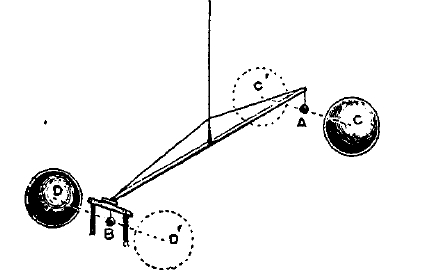
Рис. 2.

2) Способ крутильных весов. На концах коромысла крутильных весов помещаются маленькие шарики А и В (рис. 2); два массивных шара С и D, которые могут быть переведены в положение G'D', помещаются рядом; по отклонению коромысла определяется сила притяжения между шариками А и В массивными шарами. Этот опыт был впервые произведен Кавендишем,

3) Способ обыкновенных весов. На чашки весов кладут равные грузы m и m; затем под одну из чашек подкатывают массивный шар М. Наблюдаемое отклонение весов служит мерой взаимодействия масс m и М.  

Результаты измерений. Из определений величины G, произведенных различными методами, получается среднее значение G = 6,667·10^-8 абсолютных единиц CGS. Отсюда легко определить среднюю плотность земли. Пусть m будет масса какого-нибудь тела, находящегося на поверхности земли; мы имеем два выражения для силы притяжения f этого тела к земле; с одной стороны GMm²/R², где M — масса земли, R — ее радиус (земля принимается здесь за шар), с другой стороны mg, где g — ускорение силы тяжести. Замечая, что М=4/3 πR³Δ, где Δ — средняя плотность земли, и приравнивая друг другу оба выражения для f, получаем Δ = 3g/4πGR. Отсюда для g получаем наиболее вероятное значение 5,52. Таким образом, средняя плотность земли оказывается приблизительно вдвое больше, чем плотность горных пород, составляющих известные нам поверхностные слои земли. Это указывает на присутствие внутри земли очень плотного — по всей вероятности, железного или железно-никелевого — ядра. Для массы земли получается число 6 10²¹ тонн.

Степень точности закона Ньютона. Немногие физические законы подвергались проверке в столь обширном масштабе, как закон тяготения — от взаимодействия крупнейших небесных тел (см. небесная механика) до притяжения металлических шариков диаметром не более 2 ¼ дюйма (опыты Бойса по способу крутильных весов). Вея совокупность этих наблюдений и опытов приводит к выводу о чрезвычайной точности, с какой закон Ньютона соблюдается в природе. В частности, об этом свидетельствует возможность предсказывать на основании этого закона новые научные факты: сюда относится знаменитое предвычисление орбиты и массы Нептуна (см.). Тем не менее, существуют случаи, где вычисления, произведенные на основании закона Ньютона, несколько расходятся с наблюдениями. Наиболее крупный случай такого расхождения обнаруживается в движении перигелия планеты Меркурий (еще: в движении узла орбиты Венеры, в движении перигелия Марса и др.). Различными учеными был предпринят ряд теоретических попыток изменить форму закона Ньютона таким образом, чтобы это расхождение было устранено. Наиболее удачная из этих попыток принадлежит Герберу, который исходил из предположения, что притягательное действие одной массы на другую требует известного времени для своей передачи через пространство, разделяющее эти массы; откуда следует, что притяжение движущихся тел должно происходить по видоизмененному закону, сравнительно с притяжением тел покоящихся: в выражение закона тяготения двух масс должна входить их относительная скорость. Гербер пришел к замечательному результату, что расхождение в случае движения перигелия Меркурия устраняется вполне, если предположить, что скорость распространения силы тяготения равняется скорости света (300000 км/с). См. также планеты и луна.

Попытки объяснения силы тяготения. Тяготение остается до сих пор одной из наиболее таинственных сил природы, несмотря на то, что многими учеными делались попытки свести явление тяготения к тем или другим более понятным основаниям. Неясен ответ даже на наиболее основной вопрос: представляет ли тяготение собой actio in distans, т. е. распространяется ли действие его без всякого посредствующего агента, или же передача силы тяготения совершается через посредство некоторой среды, вроде эфира? С одной стороны, методы мышления современных физиков упорно противятся допущению всякого actio in distans; но с другой, в случае тяготения до сих пор не является установленным ни один из трех критериев, которые служат фактическими доказательствами роли среды в передаче силы: 1) не доказано, что тяготение требует времени для своего распространения; 2) не доказано, что действие силы тяготения зависит от характера среды, разделяющей друг от друга взаимно тяготеющие тела; 3) не доказано, что эта промежуточная среда сама испытывает какие-либо изменения, находясь в поле сил тяготения.   Из попыток объяснить тяготение механическими причинами назовем: а) теорию Ломоносова-Лесажа, по которой взаимное притяжение тел есть результат толчков, испытываемых этими телами от носящихся в пространстве частиц особой  материи; б) гидродинамические теории, разрабатываемые в направлении, впервые указанном Бьеркнесом; в) но наиболее согласуются с духом современной физики воззрения, объясняющие тяготение действием электромагнитных сил. Одна из более ранних попыток этого рода принадлежит Цёльнеру; он предположил, что каждый материальный атом содержит в себе положительный и отрицательный электрические заряды, причем притяжение противоположных зарядов несколько сильнее, чем отталкивание зарядов однородных; отсюда между каждыми двумя материальными атомами возникает равнодействующая сила, имеющая характер притяжения. Быть может, нет надобности даже допускать перевес притяжения над отталкиванием в той форме, как это делает Цёльнер; может быть, достаточно (по примеру Штарка) принять в расчет взаимодействие неупорядоченных электромагнитных полей, свойственных двум материальным телам, чтобы объяснить тяготение этих тел. Интересно отметить, что допущение электромагнитной природы тяготения ведет к следствию, что сила тяготения распространяется в пространстве е той же скоростью, с какой распространяются электромагнитные возмущения (а значит — и свет). Однако все это — не более как догадки; сколько-нибудь прочного и общепринятого объяснения тяготения до сих пор не существует. См. притяжение.

А. Бачинский.