Циссоида

Циссоида, плоская кривая линия, изобретенная греческим ученым II в. до н. э. Диоклесом для геометрического решения знаменитой в древности задачи об удвоении куба.

Циссоида может быть начерчена следующим образом: строят круг с диаметром ОА=а и в точке А к нему касательную; из точки О проводят к кругу секущие линии до касательной и на каждой секущей ОD откладывают от точки О отрезок ОВ, равный расстоянию между кругом и касательной CD; геометрическое место точек В и будет циссоида; из построения видно, что она имеет острие в точке О и две совершенно симметричные ветви относительно диаметра ОА, простирающиеся в бесконечность и неограниченно приближающиеся к касательной UV, которая служит для циссоиды ассимптотой. Уравнение циссоиды легко вывести в полярных координатах: обозначая радиальный вектор ОВ через r, а угол ВОА = φ, имеем

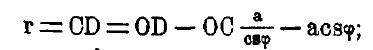
или r = asn²φ/cs φ; переходя к прямоугольным координатам, получим х = а.y²/r², или x = ay²/(x²+y²); x³=(a-x)y², что можно представить в виде:

Т.о., циссоида – кривая  3-го порядка. Для удвоения с помощью циссоиды куба с ребром а, откладываем на оси OY отрезок ОЕ=2а, соединяем точку Е с точкой А и через точку пересечения   М линии ЕА с циссоидой проводим прямую ON до встречи с касательной AU; тогда AN и будет стороной куба вдвое большего объема, чем а³. Действительно:

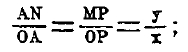
с другой стороны:

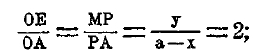
но по свойству циссоиды:

откуда, так как MP/OP = AN/OA находим:

Откладывая по оси 0U отрезки За, 4а, 5а…, мы подобным же образом получили бы на касательной AU отрезки длиной

циссоида обладает многими интересными геометрическими свойствами; так, площадь между бесконечными ветвями кривой и касательной UV равна утроенной площади производящего круга. Поэтому, циссоида была предметом изучения многих ученых, в частности Ньютона, указавшего способ для черчения ее непрерывным движением.

И. Ч.