Универсальный гониометр

Универсальный гониометр простейшего устройства изображен в статье специальные отделы кристаллографии (см. XXV, 619/20, прил., 1/2). Здесь слева видна зрительная труба на столбике, установленном на треножнике. Ось ее направлена на центр прибора, в котором помещается измеряемый кристалл. В этом центре пересекаются под прямым углом обе оси вращения прибора: вертикальная, неподвижная, и горизонтальная, вращающаяся в горизонтальной плоскости вместе с подвижной частью прибора (изображенной с правой стороны). Значение неподвижной и подвижной оси, а вместе с тем и величины углов, отсчитываемых на соответствующих лимбах, весьма различное. Значение их наглядно выступает, если по этим отсчитанным углам мы определим для каждой грани изображающую ее (в гномостереографической проекции) точку; для такого изображения особенно удобны издающиеся с этой целью стереографические сетки.

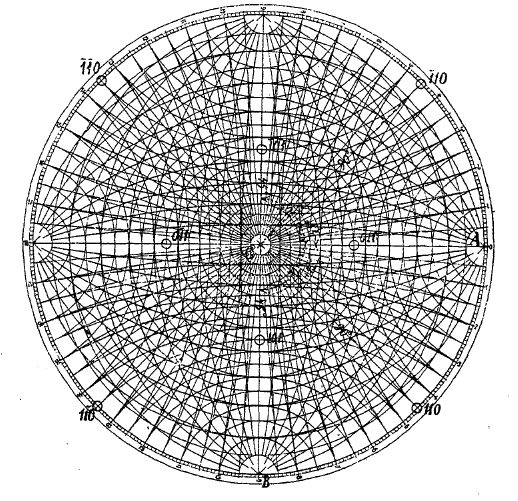
Образчик такого изображения дан на прилагаемой фигуре и относится к граням ромбического додекаэдра (ср. XXV, 587, фиг. 2). Каждую грань кристалла можно отметить особенными символами (ср. XXV, 601). Все грани этой формы выразятся символами из трех целых чисел, из которых одно есть ноль, а два другие представляют единицы. Если бы в этой форме присутствовала горизонтальная грань, она выразилась бы в проекции точкой С, то есть центром. Такой грани не имеется, но имеются четыре вертикальные грани, в разрезе представляющие квадрат, то есть взаимно-перпендикулярные. Мы легко найдем  их  изображения по символам (110), (1̄10), (1̄1̄0) и (110). Четыре же наклонные (под углом 45° к вертикальной оси) изображены точками с символами (011), (101), (011) и (1̄01).

При измерении этой формы на гониометре мы для каждой получим два числа, по одному на каждом из лимбов, и точки, изображающие эти грани, найдутся по этим углам, из которых тот, который относится к подвижной оси, отсчитывается по диаметрам, считая за начальный, например, диаметр СА. Второй же отсчет, соответствующий неподвижной (вертикальной) оси, непосредственно даст угол наклона, считая от горизонтальной, изображаемой точкой С в центре. Для всех четырех наклонных граней угол этот один и тот же, а именно 45°, а для вертикальных этот угол 90°. Как определяющие точки на сетке (т. е. в сущности, на сфере), числа эти называются сферическими координатами граней, а, как видим теперь, значение обеих координат весьма различно, почему должно отличать первую координату от второй. Например, для грани (110), первая координата + 46°, а вторая 90°; для грани (11̄0) первая координата —45°, а вторая 90°; для грани (101) первая координата +90°, а вторая 45°; для грани (1̄01) первая координата -90˚, а вторая 45° и т. д. Сказанным достаточно характеризуется приложение универсального метода к гониометрическому исследованию кристаллов, и одновременно раскрывается, какое облегчение доставляют при этой работе стереографические сетки.

В приложении к исследованию оптических свойств кристаллов универсальный метод дал возможность заменить употреблявшиеся до его появления пластинки, вышлифованные из кристалла строго определенным образом, пластинками, вышлифованными совершенно произвольно (или случайно). Чтобы понять значение этой замены, достаточно указать на следующие два обстоятельства: 1) вышлифовать пластинку из твердого вещества нетрудно, но трудности вышлифовывания таких пластинок в одном строго определенном направлении так велики, что, несмотря на сооружавшиеся с этою целью весьма сложные (и дорогие) шлифовальные приборы, цель все-таки не достигалась вполне; к этому нужно присоединить необходимость иметь вещество именно в форме не слишком маленького кристалла, что также осуществляется довольно редко, а если вещество новое, то только путем ряда приближенных исследований удается определить то именно направление, в котором нужно вышлифовать пластинку; 2) при исследовании горных пород с пятидесятых годов прошлого века (по почину английского петрографа Сорби) для исследования их вышлифовываются пластинки толщиной 0,02—0,03 мм, и в этот шлиф попадают разрезы даже не десятков, а сотен слагающих породу минералов, и, конечно, все эти разрезы имеют случайный характер, и, можно сказать, даже значительная затрата времени для отыскания разреза в нужном направлении редко приводит к положительному результату, и таким образом материал остается недостаточно использованным для научных целей, несмотря на значительную, но недостаточно производительную затрату труда.

Упомянутый универсальный столик представляет собой укрепляющийся на обыкновенном столике микроскопа маленький теодолитик, в центре которого помещено круглое стекло, заменяющее обыкновенный столик микроскопа, но по устройству прибора способный подвергаться вращению около трех перпендикулярных осей; на нем и помещается исследуемый препарат; с обеих сторон насаживаются стеклянные сегменты, так рассчитанные, чтобы образовался стеклянный шар, в центре которого и помещается исследуемая пластинка; чрез этот же центр проходят все (конечно, не материальные, а воображаемые, как и в гониометре) оси вращения.

По закону Френеля (ср. XXV, 610), оптические свойства кристалла выражаются эллипсоидом, величины осей которого пропорциональны показателям преломления в  этих главных направлениях, а из этих величин уже математически выводятся положения обоих круговых сечений эллипсоида, перпендикуляры к которым весьма легко устанавливаются на опыте в виде т. н. оптических осей.

В поляризационном микроскопе при обыкновенной установке николей (анализатора и поляризатора) в скрещенном положении поле зрения темно, и вообще освещение и окраска появляется с введением в это поле кристаллических пластинок. Но если мы введем пластинку так, чтобы одна из осей оптического эллипсоида была параллельна подвижной оси А, то по закону Френеля не только поле останется темным, но будет продолжать оставаться темным и тогда, когда мы будем вращать пластинку около той же оси. Так дается возможность распознать положение осей эллипсоида в кристалле.

Если ось эллипсоида наклонна, то простым вращением пластинки в своей плоскости можно такую ось привести в положение вертикальной плоскости СА. Пусть, например, эта ось наклонена под углом 45° и выражается тою же точкою на сфере, что отмечена символом (011). В таком случае, вращая пластинку около вспомогательной горизонтальной оси В, мы можем ось эллипсоида привести к совмещению с осью А, и поле станет темным и останется таким при вращении около этой оси.

Кроме статей и сочинений автора, с течением времени появились и весьма солидные книги с изложением универсального метода и достигнутых им результатов. К числу таких относится книга М. Л. Усова, «Федоровский, или универсально-оптический метод исследования породообразующих минералов» (1910). Но особенной полнотой отличается книга В. В. Никитина, переведенная на французский язык и вышедшая в Женеве по частям (I и II часть в 1914 г.) под заголовком «La méthode universelle de Fedoroff» (trad, par prof. L. Dupаrc et Vera de Derwies).

По странной игре случайностей первые применения этого метода были сделаны не в ученых кабинетах университетов или высших школ, а в музее Турьинских рудников (в 1894 г.), лежащих недалеко от границ населенности по Уралу и даже теперь связанных с остальным цивилизованным миром только ветвью заводской железной дороги.

Е. Федоров.