Уравнение

Уравнение. Уравнением называется равенство, в котором левая часть не равна тождественно правой, так что равенство имеет место (удовлетворяется) только при частных значениях некоторых входящих в него количеств, называемых неизвестными. Значения неизвестных, при которых равенство имеет место, называются решениями, или корнями уравнения. По числу неизвестных уравнения разделяются на уравнения с одним, двумя и т. д. неизвестными. Два уравнения называются равносильными, если они имеют одинаковые решения. Если дано уравнение А=В, где А и В суть функции неизвестных, то можно доказать, что уравнение А+D=В+D, АC=ВС (С≠0) равносильны данному; например: уравнение

3x – 8 = 2x + 2 и уравнение 3x – 2x = 2 + 8; уравнение (x-2)/5 = x/10 и уравнение 2(x-2) = x.

Поэтому всякое уравнение можно привести к виду f(х, у, z,...)=0, где f не содержит дробей, и х, у, z,... — неизвестные. Так как в число решений уравнения Аⁿ=Вⁿ (n — целое) входят все решения уравнения А=В, то возведением в степень можно уничтожить все радикалы в уравнение; например: √(x—2)=3 и х—2=9. Если после этого левая часть уравнения f(х, у, z,...)=0 будет многочленом, то уравнение называется алгебраическим, и измерение относительно х, у, z,... его высшего члена называется степенью уравнения, в отличие от уравнения трансцендентных, каково, например, уравнение sin х=0. Решение одного уравнения со многими неизвестными есть задача неопределенная, так как такое уравнение удовлетворяется непрерывной последовательностью решений; чтобы решения были уединенными вообще, должно быть дано столько уравнений, сколько неизвестных. Совокупность уравнений, удовлетворяющихся одними и теми же значениями неизвестных, называется системой совместных уравнений. Можно доказать (теорема Даламбера), что всякое алгебраическое уравнение n-ой степени a₀xⁿ + a₁x^n-1 +…+ a_n-1x+a_n = 0 имеет n действительных или мнимых решений, причем решения общего уравнение первой..., четвертой степеней выражаются явно в функции их коэффициентов. Например:

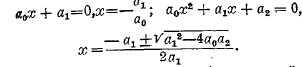
Уравнения высших степеней вообще неразрешимы в радикалах (теорема Абеля), и их приходится решать приближенными методами; эти методы излагаются в высшей алгебре. Если не требуется большой точности, то можно определить действительные решения уравнения f(х)=0 графически, вычерчивая кривую у=f(х) и определяя на чертеже абсциссы ее точек пересечения с осью абсцисс у=0. Трансцендентное уравнение может иметь бесконечное множество решений: например, sinx= ½; здесь x = π/6 + 2kπ (k — любое целое число). Системы уравнения первой степени проще всего решаются при помощи определителей. Например: ах+bу=с,

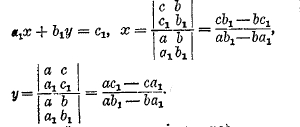
Система высших степеней – приведением различными приемами к одному уравнению с одним неизвестным. Если не требуется большой точности, то можно получить решение, например, уравнение f(х, у)=0, φ(х, у)=0, графически, вычерчивая линии f = 0, φ  = 0 и определяя на чертеже координаты точек пересечения этих линий. См. курсы элементарной и высшей алгебры.

Уравнения дифференциальные см. исчисление бесконечно малых. Уравнения интегральные суть уравнений вида

где даны функции  ψ и k (ядро) и требуется найти функцию φ; λ, а, b — постоянные; эти уравнения, введенные недавно Фредгольмом, играют большую роль в математической физике. Литература весьма обширна. См. Heywood et Fréchet, «Les équations intégrales».

А. Некрасов.