Векториальный анализ

Векториальный анализ, исчисление, имеющее своим объектом векторы в том же смысле, в каком обыкновенный математический анализ оперирует над числами.

В механике и в физике мы встречаемся с величинами двоякого рода. Величина первого рода вполне определена, если она задана числом, выражающим ее в соответствующих единицах; таковы длина, площадь, объем, масса, плотность, температура, теплоемкость и т.д.; эти величины называются скалярами. Величины второго рода известным образом ориентированы в пространстве и потому одним численным заданием не определяются; таковы скорость, ускорение, сила, моменты вращения; эти величины называются векторами. Чтобы определить силу, недостаточно указать ее численную величину, нужно еще определить ее направление. Сообразно этому силу изображают отрезком, длина которого выражает величину силы, а направление указывает направление действия силы. Таким образом, и всякий вектор изображается отрезком, имеющим определенную величину и направление; для геометра этот отрезок и есть вектор.

Всякий отрезок (а, следовательно, и вектор) определяется проекциями на три оси; поэтому и вектор может быть задан численно, но не одним числом, а тремя числами, выражающими его проекции на три оси.

При всяком изучении векториальных величин приходится определенным образом комбинировать векторы, переходить от одних векторов к другим, по некоторым данным векторам строить новые результирующие векторы: по слагающим силам приходится определять равнодействующую, по данным силам и осям приходится определять моменты этих сил и т.п. Все эти операции можно сводить к арифметике и к анализу, в том смысле, что проекции искомого вектора могут быть вычислены арифметически по данным проекциям исходных векторов. Так, если X, Y, Z суть численно заданные проекции одной силы, X′, Y′, Z′ - проекции другой силы, то X + X′, Y + Y′, Z + Z′ суть проекции равнодействующей. При более серьезных вычислениях этот путь осложняется в большой мере тем, что в каждом случае приходится делать три вычисления - разыскивать численно три проекции. Даже равенство двух векторов выражается не одним, а тремя уравнениями, устанавливающими в отдельности равенство соответственных проекций; например, чтобы выразить, что приведенные выше две силы равны, нужно написать X = X′, Y = Y′, Z = Z′. В целях упрощения этого процесса мы приходим к мысли производить операции непосредственно над векторами, подобно тому, как мы в арифметике производим действия над числами. Осуществление этой идеи и приводит к алгебре векторов, а дальнейшее ее развитие - к векториальному анализу.

Два вектора считаются равными, если имеют одинаковую величину и направление; иначе говоря, если отрезки имеют одинаковую длину, параллельны и обращены в одну и ту же сторону (отрезки АА′ (а) и ВВ′ (b) на (рисунке 1); они могут, следовательно, отличаться один от другого только начальной точкой. Алгебра векторов устанавливает понятия о сумме, разности, произведении и частном двух векторов, подобно тому, как в арифметике устанавливаются те же понятия в применении к числам. Положим, что нам дано несколько векторов, скажем, а, b, с (рисунок 2). От произвольной точки А, как начальной, строим вектор, равный данному вектору а; из конечной точки А′ проводим вектор А′В′, равный второму данному вектору b, из конечной точки В′ проводим вектор В′С′, равный третьему вектору с. Вектор AC′ (s), идущий от начальной точки А к конечной - С′, называется суммой векторов а, b, с и обозначается, как и в арифметике, символом s = a + b + c. Эту сумму векторов часто называют геометрической суммой, чтобы оттенить ее отличие от арифметической суммы чисел. Точно также, чтобы отметить, что символы а, b, с, s означают не числа, а векторы, их обыкновенно отмечают черточками сверху или жирным шрифтом. Равнодействующая нескольких сил выражается геометрической суммой векторов, изображающих слагающие силы.

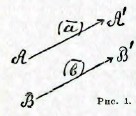
Рис. 1

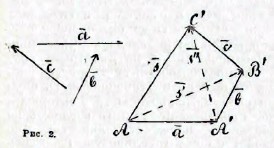
Рис. 2

Разность двух векторов ā и b̄ определяется как такой вектор c̄, который нужно прибавить к вектору b̄, чтобы получить вектор ā; то есть c̄ = ā - b̄, если ā = b̄ + c̄. Легко видеть, что на рисунке 2

S’ = ā + b̄, а потому b̄=ŝ’ – ā;
ŝ = ŝ’ + c̄, а потому c̄ = ŝ – ŝ’.

Основные свойства арифметической суммы, из которых разматываются все свойства суммы и разности, заключаются в так называемых переместительном и сочетательном законах, которые выражаются тождествами:

a + b = b + a; a + (b + c) = (a + b) + c.

Эти соотношения остаются в силе, как в этом легко убедиться, и в применении к геометрической сумме векторов. Так, на рисунке 2 мы видим, что

Ŝ = ā + b̄ + c̄ = ŝ’ + c̄, где ŝ’ = ā + b̄,

так что ŝ = (ā + b̄) + c̄ и в то же время ŝ = ā + ŝ”, где ŝ” = b̄ + c̄,

так что ŝ = ā + (b̄ + c̄),

а потому ā + (b̄ + c̄) = (ā + b̄) + c̄

Вследствие того, что эти основные законы остаются в силе, выражение, представляющее результат геометрического сложения и вычитания векторов, может быть подвергнуто всем тем преобразованиям, какие допустимы в так называемой алгебраической сумме. В пределах сложения и вычитания арифметика векторов формально совпадает с арифметикой чисел. Но дело обстоит сложнее при умножении. Под произведением из вектора ā на положительное число α разумеют вектор (α . ā), который имеет то же направление, что и вектор ā, но длина которого увеличена в а раз. Под произведением из вектора ā на отрицательное число -α разумеют вектор α . ā, повернутый на 180°, то есть взятый в противоположном направлении. Эти произведения из векторов на числа все еще подчиняются тем же формальным законам, что и арифметические произведения. Но дальнейшее развитие тех же идей приводит нас к перемножению векторов. Установить понятие о произведении двух векторов так, чтобы такого рода произведения сохранили все основные свойства произведения чисел, не удалось. Напротив, установлены двоякого рода произведения векторов - скалярное и векториальное. Каждое из этих произведений сохраняет одни свойства арифметического произведения и теряет другие.

Пусть ā и b̄ будут два вектора, α и β - числа, выражающие их длины в одной и той же линейной единице, ω - угол между направлениями векторов. Под скалярным произведением векторов ā и b̄, которое мы будем здесь отмечать символом ā×b̄, разумеют число αβCosω.

Из этого определения непосредственно ясно, что скалярное произведение обладает свойством переместительности, то есть что ā×b̄ = b̄×ā; немного более внимательное размышление обнаруживает, что скалярное произведение обладает также распределительностью, то есть что (ā + b̄)×c̄ = ā×c̄ + b̄×c̄. Но закон сочетательности здесь уже не приложим, то есть соотношение (ā×b̄)×c̄ = ā×(b̄×c̄) не имеет места. Чтобы видеть, в какой мере скалярное произведение векторов отличается от арифметического, достаточно заметить, что оно обращается в нуль всякий раз, как перемножаемые векторы взаимно перпендикулярны; между тем арифметическое произведение никогда не обращается в нуль, если ни один из множителей не равен нулю.

Если материальная точка движется по прямой линии и пробегает вектор b̄, а в числе действующих на точку сил какая-либо остается постоянной и выражается вектором ā, то работа этой силы на указанном пути выражается скалярным произведением ā×b̄. Эта сила не производит работы на этом пути, если она остается перпендикулярной к траектории; скалярное произведение равно нулю.

Под векториальным произведением ā. b вектора ā на вектор b разумеют вектор, определенным образом составленный по данным векторам ā и b̄. Именно, длина этого вектора выражается числом αβ sin ω; направлен же он перпендикулярно к плоскости, определяемой векторами ā и b̄, и притом так, что наблюдатель, стоящий вдоль вектора ā и смотрящий на вектор b̄, видит произведение c̄ направленным слева направо (рисунок 3). Из этого определенно видно, что вектор c̄ имеет одинаковую длину, выражает ли он произведение ā . b̄ или b̄ . ā; но согласно указанной ориентировке он будет во втором случае направлен не в ту сторону, как в первом, а в противоположную; иными словами, ā . b̄ = - b̄ . ā. Векториальное произведение, таким образом, не обладает переместительностью; но свойство сочетательности и здесь остается в силе, то есть (ā + b̄) . c̄ = ā . c̄ + b̄ . c̄.

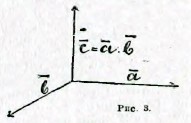
Рис. 3

Но указанное отступление уже коренным образом отражается на дальнейшем развитии операций над векторами.

Как бы на смену нарушенных тождеств обыкновенной арифметики здесь появляются новые своеобразные соотношения, например, замечательное тождество Якоби

ā . (b̄ . c̄) + b̄ . (c̄ . ā) + c̄ .  (ā . b̄) = 0

Эти новые свойства, сплетаясь с сохранившимися обычными свойствами суммы, разности, произведения, частного, и составляют своеобразную арифметику или, как принято не совсем правильно говорить, - алгебру векторов. Но отсюда только один шаг к анализу.

Как мы различаем постоянные и переменные величины, выраженные численно, так можно различать также постоянные и переменные векторы. Представим себе постоянную точку О (начало) и движущуюся - А; тогда каждому положению точки А будет соответствовать определенный вектор OA - ее радиус-вектор; этот вектор будет, очевидно, меняться с положением точки А, это переменный вектор. Если точка А описывает кривую, и s есть скаляр - число, выражающее длину кривой от некоторой постоянной точки АO, то при движении точки А изменяется s, и каждому значению s отвечает определенный радиус-вектор OA (r̄) (рисунок 4). Вектор r̄ является функцией скаляра s; r̄ = f(s). Вообще, относя каждому значению некоторого скалярного переменного s вектор r̄, мы приходим к функциональной зависимости между вектором и скаляром. Изучение этой зависимости составляет предмет векториального анализа подобно тому, как обыкновенный анализ изучает численно заданные функции. Если вектор r̄ есть функция скаляра s, то три его проекции - вернее, числа х, у, z, выражающие длины этих проекций - также суть функции от s и векториальная зависимость r̄ = f(s) эквивалентна трем числовым зависимостям x = g (s), y = h (s), z = k (s).

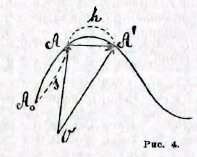
Рис. 4

В этом замещении трех функций одной векториальной функцией и заключается сила векториального анализа.

Положим, что мы дадим независимой переменной в рассмотренной выше зависимости r̄ = f(s) (рисунок 4) сначала значение s, а потом наращенное значение s + h; этим значениям будут отвечать векторы OA = f(s) и ОA′ = f(s + h). Вектор АА′ = OА′ - OA представляет собой геометрическое наращение, которое получает переменный вектор, когда независимая переменная получает наращение h, то есть AA′ = f(s + h) - f(s). Если мы разделим это наращение на h, то получим вектор, который при положительном h направлен в ту же сторону, что АА′, при отрицательном - в противоположную. Когда h стремится к нулю, то отношение

AA’/h = (f(s+h)-f(s))/h

может стремиться к определенному предельному вектору; этот предельный вектор (буде он существует) называется геометрической производной вектора r̄. Если A есть движущаяся точка, то геометрическая производная ее радиуса-вектора представляет собой скорость движения, геометрическая производная скорости есть ускорение.

Геометрические производные сохраняют многие свойства обыкновенной производной (см. высшая математика и дифференциальное исчисление); например, в силе остаются правила составления производной суммы и векториального произведения. Что наиболее замечательно, при надлежащих условиях остается в силе формула Тайлора. Другие свойства обыкновенных производных в векториальном анализе изменяются - и таким образом получается своеобразное дифференциальное исчисление векторов, из которого в том же порядке идей получается интегральное исчисление. Обе дисциплины отличаются необычайным изяществом и чрезвычайно богаты приложениями к геометрии, механике и теоретической физике.

Как мы видели на рисунке 4, радиусом-вектором r̄ вполне определяется положение точки А (при данном начале O), и соотношение r̄ = f(s) можно рассматривать, как векториальное уравнение кривой. Эта замена трех уравнений аналитической геометрии одним векториальным и послужило точкой отправления векториального исчисления.

Если не считать Весселя (Wessel) и Аргана (Argand), у которых эти идеи выражены еще недостаточно определенно, то отцом векториального анализа нужно признать Мёбиуса (Möbius); в сочинении «Der baryzentrische Calcul» (1827) он устанавливает действия не над векторами, а над точками; но эти операции совпадают с преобразованиями, которым в векториальной алгебре подвергаются конечные точки векторов при действиях над ними. В сочинениях Беллавитиса (Bellavitis), особенно в его книгах «Metodo delle equipollenze» (1835) и «Sposizione del metodo delle equipollenze» (1855), установлены уже прямые действия над векторами и даны многочисленные применения к геометрии. Когда Коши, следуя Аргану, показал, что операции над векторами представляют собой геометрическую интерпретацию действий над комплексными числами, то это составило эпоху, ибо послужило наиболее сильным импульсом к всеобщему признанию комплексных величин. Однако, комплексные числа изображаются только векторами, расположенными в одной плоскости; но вскоре Гамильтон (Hamilton, «On Quaternions» 1843-1844; «Lectures on Quaternions» 1852) и Грассманн (H. Grassmann, «Die Ausdehnungslehre» - сочинение, написанное в 1844 году и совершенно переработанное в 1866 году) указали новые, высшие комплексные числа - кватернионы (см.). Каждый кватернион состоит из скалярной и векториальной части; геометрическим изображением последней служит вектор в трехмерном пространстве. Все развитие векториального анализа находится в теснейшей связи с учением о кватернионах. Однако, учение это довольно долго не встречало сочувствия среди математиков. Только, когда Дж. Максуэль (J. Maxwell, «А treatise on Electricity and Magnetism», 1873) воспользовался ими для выражения своих замечательных идей в области электродинамики, то кватернионы, а вместе с ними и векториальный анализ, получили значительное распространение, которое быстро росло по мере того, как идеи Максуэля получали преобладание. В новых трактатах по теоретической физике изложение ведется почти исключительно методами векториального анализа. Нужно, однако, сказать, что эти методы имеют и своих решительных противников.

Bucherer, «Elemente der Vektoranalysis», Leipzig, 1905; Gans, «Einführung in die Vektoranalysis», Leipzig, 1905; Ignatowsky, «Die Vektoranalysis», Leipzig, 1909-1910; П. О. Сомов, «Векториальный анализ и его приложения», Спб., 1907 г.

В. Каган.