Веревочный многоугольник

Веревочный многоугольник (иначе называемый нитяным) употребляется в графостатике вместе с силовым для графического (посредством одного чертежа, без вычислений) сложения или разложения сил параллельных и пересекающихся. Положим, дано сложить три силы: Р₁, Р₂ и Р₃, данные на чертеже.

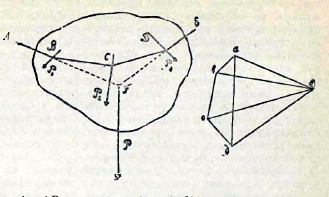
Строим сначала силовой многоугольник abсd, для чего проведем линию ab параллельно силе Р₁ и отложим на ней ab = Р₁, затем далее bс ll Р₂, cd II Р₃; тогда замыкающая сторона ad этого многоугольника, называемого силовым, выразит равнодействующую наших сил по величине и направлению. Чтобы определить точку приложения равнодействующей на данном теле, поступаем так: берем произвольную точку е (полюс) и соединяем ее с вершинами силового многоугольника. Затем берем где-либо точку А и через нее проводим АВ II ае до пересечения с силой Р₁, через В проводим ВС II be, через С проводим CD II се и т.д. Получаем разомкнутый многоугольник, который и называется нитяным или веревочным, так как веревка приняла бы под действием наших сил как раз эту форму. Теперь, если продолжим линии АВ и DE до их взаимного пересечения в точке F, то через эту точку и пройдет наша равнодействующая, что и выражаем, откладывая Р II ad. Применение веревочного многоугольника при сложных конструктивных расчетах значительно облегчает задачу, заменяя сложные вычисления сравнительно простым вычерчиванием.