Винт (винтовая линия)

Винт. Винтовая линия образуется навертыванием плоского прямоугольного треугольника abc на круглый цилиндр (фиг. 1). При этом катет ca займет на цилиндре положение окружности cd′f′h′c, т. е. пересечения цилиндра с плоскостью, перпендикулярною к его оси. Другой катет ab совпадет с одной из образующих цилиндра; в частности, если длина катета ca равна длине окружности cd′fh′c, то катет ab займет положение образующей cb′. Наконец, гипотенуза cb обратится в винтовую линию ce′g′i′b′. При этом всякий раз дуги cd′, cf′... соответственно равны отрезкам cd, cf..., а отрезки образующих d′e′, f′g′... соответственно равны перпендикулярам de, fg...; то же самое имеет место и для всяких промежуточных дуг и отрезков образующих. Угол α наклона образующей прямой с к катету основания са, иными словами угол между касательной к винтовой линии и касательной к кругу основания, называется углом наклона винтовой линии. Радиус цилиндра называется радиусом винтовой линии. Если представить себе, что гипотенуза cb продолжается неопределенно далеко, то винтовая линия окажется также не определенно длинной; если при этом длина катета ас равна 2πr, где r - радиус винтовой линии, то, начиная от точки b кверху и начиная от точки с книзу, на цилиндре будут повторяться те же относительные расположения точек винтовой линии, которые имели место в пределах первого оборота се′g′i′b′: последний как бы продвигается вдоль оси на величину сb, равную катету а в то время, когда катет ас = 2πr. Эта длина катета ab, или иначе - расстояние, считая по образующей, между двумя одноименными точками одной и той же винтовой линии, называется ее шагом. Из треугольника abc видно, что между шагом t, радиусом r и углом наклона α существует соотношение: t = 2πr∙tgα . Изображенная на фиг. 1 винтовая линия представляется наблюдателю поднимающейся на видимой поверхности цилиндра влево; такая линия называется левой. Мы получили бы правую винтовую линию, если бы стали навертывать треугольник cab в противоположную сторону, или если бы, при том же направлении навертывания, имели треугольник сb′а, а не cab.

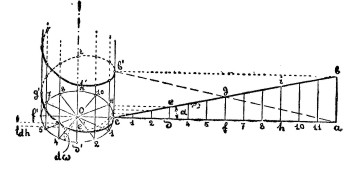
Фиг. 1

Образование винтовой линии можно представить себе также движением, на круглой цилиндрической поверхности некоторой точки так, чтобы всякому ее угловому перемещению dω соответствовало определенное поступательное dh вдоль по образующей; при этом путь, пройденный по кругу основания, есть rdω, а отношение dh/rdω представит тангенс угла наклона действительно пройденного точкой отрезка винтовой линии к кругу основания. Если этот угол по мере движения точки не меняется, т. е. если dh/rdω = tgα = const, то получается рассмотренная выше винтовая линия постоянного шага. В общем же случае можно представить себе это отношение переменным; равным образом можно вообразить, что точка движется, вращаясь около оси и вдоль ее, но остается не на поверхности круглого цилиндра, а на какой-нибудь другой поверхности вращения, например на конусе, на однополом гиперболоиде вращения, на эллиптическом цилиндре и т. д.; всякий раз точка будет описывать на этих поверхностях кривые, носящие общее название винтовых линий. Наибольшее практическое значение имеет винтовая линия постоянного шага, начерченная на круглом цилиндре.

Вообразим прямую, проходящую через какую-нибудь точку винтовой линии и через ее ось, пересекая последнюю в общем случае под острым углом. Если эта прямая начнет двигаться, оставаясь всегда на винтовой линии и всегда пересекая ее ось под одним и тем же углом, то она опишет в пространстве винтовую поверхность. Эта поверхность будет постоянного или переменного шага, правой или левой, смотря по тому, каково было наименование направляющей винтовой линии; также эта поверхность будет прямоугольной (фиг. 2) или остроугольной (фиг. 3) (также косой), смотря по тому, был ли угол между образующей линией и осью прямым или острым (на фиг. 2-3 представлены только передние половины левых винтовых поверхностей; при этом на фиг. 2 слева видна верхняя часть поверхности, а справа - ее нижняя часть). Винтовые поверхности имеют широкое практическое применение: ими ограничиваются поверхности винтов и гаек; ими очерчиваются поверхности гребных винтов, воздушных пропеллеров; они применяются во многих случаях в ветряных и водяных двигателях; ими пользуются при образовании поверхности отвалов у плугов и т. д.

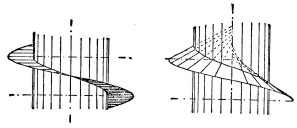
Фиг. 2,3

Если по винтовой линии перемещать целую плоскую фигуру, при условии чтобы эта плоскость всегда проходила через ось винтовой линии, то получается на сплошном теле винтовая нарезка (или резьба) винта, а внутри полого тела - дополнительная для первой - винтовая нарезка гайки. Из предыдущих определений следует, что если держать неподвижно перед собой винт, глядя на него вдоль оси, и если навернутой на него гайке дать вращательное движение по часовой стрелке, то она на правом винте будет удаляться от наблюдателя, а на левом - приближаться к нему. Смотря по виду плоской фигуры, употребленной для образования нарезки, различают прямоугольную, остроугольную и т. д. нарезки (см. болт). На протяжении одного шага винтовой линии можно размещать несколько профилей (фиг. 4): винтовая линия aa′e имеет шаг ae и на нем расположено два треугольных профиля ac и cde; каждый из них образует свою нитку аbс - а′b′с - efg; также cde - с′d′е′ и т. д. В пределах шага винта можно размещать только целое число ниток; по их числу различают число оборотов винта: на фиг. 4 изображен двухоборотный винт. Винты более чем в 6 оборотов не употребляются.

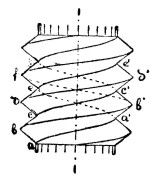
Фиг. 4

Винт и гайка употребляются не только как средство соединения двух деталей, но также входят в состав многих винтовых механизмов; все они могут быть получены путем видоизменения основного общего винтового механизма, состоящего из 3 отдельных винтовых пар, имеющих одну и ту же геометрическую ось (см. кинематическая пара). Заменяя последовательно то одну, то другую из них парами вращательными или поступательными и делая неподвижным то одно, то другое звено, получают всевозможные винтовые механизмы.

Фиг. 5
На фиг. 5 представлена схема так называемого дифференциального винта: на центральном стержне aa нарезаны две одноименные резьбы разных шагов. Гайка bb′ имеет призматический выступ b′, не позволяющий ей вращаться относительно гайки c. Если сделать bb′ неподвижным, а винт повернуть на целый оборот, то гайка с приблизится к b (или удалится от нее, смотря по направлению вращения и по наименованию резьбы) на разность шагов обеих резьб. Имея возможность вращать винт на малую долю целого оборота и делая разность шагов достаточно малой, например, в 1 mm, можно устанавливать с любой степенью точности тело, связанное с гайкой с, относительно тела, связанного с гайкой b. Если обе нарезки винта aa разноименные, то за один его оборот обе гайки b и с сближаются или раздвигаются на сумму шагов. Таковы механизмы вагонной стяжки, медведки (фиг. 6) и т. п.

Фиг. 6
Чаще всего употребляются винтовые механизмы, содержащие в своем составе только одну винтовую пару; третье тело, замыкающее механизм, должно иметь относительно винта и относительно гайки или только поступательное, или только вращательное движение, притом последнее вокруг оси винта. Таковы, например, параллельные тиски (фиг. 7), в которых челюсть A представляет гайку; перемещаясь параллельно неподвижной челюсти В, она приближается к ней или удаляется от нее, если вращать винт С в ту или другую сторону; винт С своими точеными цилиндрическими частями лежит в высверленных отверстиях челюсти В и стойки D и может в них вращаться; его поступательные движения устранены благодаря заплечику E с одной стороны и пяте F - с другой.

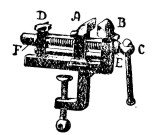
Фиг. 7

В винтовом домкрате (фиг. 8) вертикальному винту A даны оба движения - и вращательное и поступательное; неподвижной сделана гайка В; головка С, поддерживающая груз, опирается на точеный торец винта, так что может вращаться около него; механизм замыкается, если грузу так или иначе не позволить вращаться относительно гайки В, например, постановкой груза на два домкрата. Видный на фиг. 8 лежачий винтовой механизм употребляется для горизонтальных передвижений подъемного винта и по своему устройству вполне аналогичен с механизмом тисков. Наконец, в механизме французского ключа (фиг. 9) челюсть А, кончающаяся нарезным стержнем, ходит взад и вперед внутри челюсти B, если вращать гайку С, которая, благодаря двум заплечикам, может вращаться относительно челюсти В, но не имеет поступательного перемещения.

Фиг. 8

Фиг. 9

Ведущим звеном механизма может быть и винт, и гайка, но в громадном большинстве случаев механизм употребляется для преобразования вращательного движения в поступательное, а не наоборот. Одним из редких исключений является механизм дрили (фиг. 10), содержащий трех- и даже четырех-оборотный винт, которому сообщается вращательное движение то в одну, то в другую сторону благодаря быстрым движениям взад и вперед гайки А; пуговицу В держат в руках; в больших моделях ее заменяют доской, в которую удобно упереться грудью, так что для движения гайки А освобождаются обе руки.

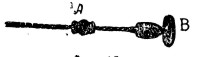
Фиг. 10

Соотношение между путем, пройденным образующей точкой по окружности основания винта и вдоль по его оси за один оборот установлено выше: t=2πr∙tgα; если иметь ввиду какой-нибудь путь по окружности s, то соответствующий путь в осевом направлении s′, будет также s, = s tgα. Пусть сила Р′ действует по касательной к кругу основания винта на радиус r, а сила Q пусть действует на гайку вдоль оси винта. По закону сохранения энергии и с пренебрежением всех вредных сопротивлений, имеем: P′s=Qs′, a потому Р′=Qtgα; т. е. при малом наклоне резьбы винт позволяет малыми силами Р′ уравновешивать большие усилия Q. Если принять во внимание трение, между винтом и гайкой, то оказывается, что эффект трения в прямоугольной резьбе сводится как бы к увеличению угла наклона резьбы а на величину угла трения ρ в том случае, когда речь идет о подъеме груза Q силой Р (или более обще - когда путь вдоль оси проходится в сторону, противоположную направлению осевой силы); и наоборот, оно сводится к такому же уменьшению угла наклона резьбы, если груз спускается на винте, так что сила Р, на плече r, уравновешивающая осевую силу Q, определяется так: P=Qtg(α±ρ). Верхний знак соответствует подъему (трение увеличивает усилие, потребное для подъема), нижний знак соответствует спуску (трение уменьшает то усилие, которое нужно приложить к грузу, чтобы он не соскользнул по винту вместе с гайкой). В тех винтах, у которых α<ρ, т. е. угол наклона меньше угла трения (около 5-6° при обычных условиях смазки), гайка сама уже не может соскользнуть с винта, какая бы осевая сила на нее не действовала: тогда для спуска груза по такому винту нужно не удерживать гайку от вращения, а, напротив, помогать ей вращаться, что видно из отрицательного знака, который получается у P. Такие винты называются самотормозящими; в тисках, подъемных механизмах и т. п. случаях они-то и должны употребляться, если не делать никаких дополнительных тормозов или задержек.

При резьбе треугольной, трапецоидальной и т. п. трение еще более заметно, нежели в прямоугольной, так как при одной и той же величине осевого усилия нормальное давление между винтом и гайкой, а вместе с ним и сила трения, в остроугольной резьбе больше, чем в прямоугольной. Поэтому последняя употребляется преимущественно в винтах, передающих движение, а остроугольная - преимущественно в винтах скрепляющих.

Коэффициент полезного действия винтового механизма определяется не только потерями работы на трение в резьбе, но также потерями работы во всех прочих трущихся частях механизма - в пяте винта, в его шипах, наконец, в поступательной паре, если она явно выражена. Обыкновенно на все эти потери работы, кроме резьбы, расходуется не более 10% полезной работы, так что полный коэффициент полезного действия можно вычислять по уравнению: η = (0,9tgα)/(tg(α+ρ)). Отсюда видно, что малым углам наклона отвечают очень невысокие к. п. д.; например, при α=5° и ρ=6° (самотормозящий винт) получаем η=0,406. Наибольший коэффициент полезного действия получается при 2α+ρ=90°; так, например, при ρ=6°, α=42°, η=0,722. Но при таком крутом наклоне резьбы как усилие вдоль оси и усилие тангенциальное, так и пути по оси и по окружности мало отличаются друг от друга, так что механизмы с такими углами наклона уместны для преобразования характера движения (дриль) и бесполезны, как преобразователи усилий.

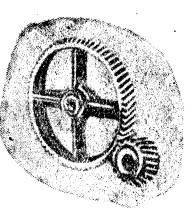
Фиг. 11

Винтовые колеса представляют частный случай зубчатых передач. Когда оси обоих колес параллельны между собой, то каждый зубец представляет из себя в полном смысле слова винтовую нарезку на круглом цилиндре (фиг. 11), но ее профиль получается из рассмотрения условий зацепления в зубчатых колесах. Главная цель таких колес - бесшумность и плавность передачи; достигается она потому, что одновременно в зацеплении находится всегда одинаковое число зубцов. Недостаток этих колес - давление вдоль оси, получающееся вследствие косого положения зубцов. Это усилие стремится сдвинуть как колесо вдоль вала, так и самый вал, почему необходимо ставить в таких случаях пяту, вызывающую как потерю в работе, так и лишний уход. Соединяя две пары таких колес, но с правыми и левыми винтовыми зубцами, вполне устраняют осевое давление на вал, зато получают сравнительно сложное устройство. Винтовые зубцы располагают также и на конических зубчатых колесах. Наконец, когда оси винтовых колес не параллельны и не пересекаются, то они получают форму винтовых зубцов, расположенных по поверхности однополого гиперболоида вращения. Если для образования колес взяты участки гиперболоида, близкие к его горловому кругу, то колеса с большой точностью можно выполнять как настоящие винтовые колеса (фиг. 12).

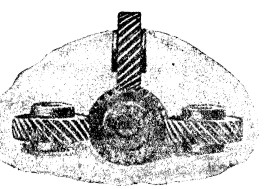
Фиг. 12

Очень часто употребляется так называемая передача бесконечным винтом, иначе - червячная передача. Она устанавливается между валами, скрещивающимися (не пересекающимися!) под прямым углом. Червяком или бесконечным винтом называется винтовая резьба, нарезанная прямо на валу или же на особом цилиндре (А на фиг. 13), который заклинивается на валу. Другой элемент передачи - червячное колесо (В на фиг. 13) - заклинивается на другом валу. Червяки, как и винты, различают по числу оборотов, или ниток, и по направлению резьбы.

Фиг. 13

Если вообразить червячное колесо бесконечно тонким и продолжить его плоскость до пересечения с червяком, то в этой плоскости получается то, что называется зацеплением с зубчатой рейкой: по мере того как червяк вращается, профиль его резьбы перемещается вдоль его оси, как того требует наклон винтовой линии, а червячное колесо вращается, как если бы этот профиль, наподобие зубчатой рейки, сцеплялся с зубцами колеса. Из этих соображений устанавливаются условия правильного профилирования червяка и червячного колеса. На червячное колесо можно смотреть как на ряд элементов резьбы гайки, вырезанных из нее двумя плоскостями, параллельными ее оси, и навернутых на тело вращения, причем ось этого тела скрещивается с осью винта под прямым углом. Тогда прежние осевые перемещения гайки, имевшие место при вращении винта, обращаются в такие же по величине перемещения по окружности червячного колеса; при этом, конечно, и соотношение между усилием P на окружности винта (червяка) и усилием Q вдоль его оси, т. е. на окружности червячного колеса, остается то же самое, а именно: P=Qtg(α+ρ), где α и ρ имеют те же значения угла наклона винтовой линии и угла трения, как и в винтовых механизмах. Если r₁ есть средний радиус винта, для которого определен угол наклона α, то на 1 оборот винта отмеченное выше меридиональное сечение винта переместится вдоль оси на величину одного шага винта = 2πr₁tgα. Если винт имеет z₁ ниток, то шаг зацепления, или расстояние между одинаковыми точками двух смежных профилей, будет t = [(2πr₁)/ z₁]tgα.

 Тот же шаг должен быть выполнен и на червячном колесе, где он повторяется столько раз, сколько на нем зубцов. Называя последнее z₂, а радиус колеса через r₂, находим что:

2πr₂ = t z₂ = 2r₁(z₂/z₁) tgα или z₂/z₁ = z₂/( r₁∙ tgα)

 Это отношение показывает, сколько оборотов сделает червяк на один оборот червячного колеса, т. к. при одном обороте червяка проходят z₁ шагов или z₂/z₁  часть полного оборота червячного колеса. Это отношение называется передаточным числом; т. к. червяки осуществляют обыкновенно одно- или двух оборотными, то такие передачи хороши там, где нужно иметь большое передаточное число в одной передаче. Это бывает необходимо, где хотят перейти от очень высокого числа оборотов к значительно пониженному, например в передачах от электромоторов (доходят до 80 зубцов на червячном колесе), а также там, где, как в подъемных механизмах, ставится задача о преодолении большого момента на валу червячного колеса М₂=Qr₂, малым моментом М₁=Рr₁=Qtg(α+ρ) r₁, на валу червяка. Отношение этих моментов M₂/M₁ = r₂/( tg(α+ρ) r₁).

 Нетрудно убедиться, что если бы не было трения в зубцах (ρ = 0), то на червяке было бы достаточно момента M₁ = M₂(r₁/r₂) tgα.

 Значит, коэффициент полезного действия механизма η = tgα/(tg(α+ρ)), т. е. тот же самый, что в винтовых механизмах. Так же как и там, его нужно уменьшить еще процентов на 10 для того, чтобы оценить потери работы в шейках и в пятах обоих валов. Из выражений передаточного числа и отношения моментов видно, что для их увеличения нужно брать малые углы наклона α; но тогда очень невелик коэффициент полезного действия (падает до 0,4) и кроме того, если α<ρ, то ведущим может быть только червяк, подобно тому, как в самотормозящем винте гайка не может быть движущим звеном. Большие углы α не употребляются и в червячных передачах, ибо тогда передаточное число мало отличается от того, которое удобно выполняется в цилиндрических или винтовых колесах. Сличая отношение моментов с передаточным числом и с к. п. д., видим, что M₂/M₁ =  (z₁/z₂)η.

 Это выражение служит исходным при расчете червячной передачи: задаваясь углом наклона червяка и выясняя затем его к. п. д. (η), зная далее величину располагаемого момента М₁ и преодолеваемого М₂, находим числа зубцов z₂, если выбрать число ниток z₁ на червяке. Определение прочных размеров червяка и его колеса делается по тем же формулам, как и в зубчатых колесах.

Подробнее см. курсы теории механизмов, например, профессора Рузского, Мерцалова и курсы деталей машин, например, Сидорова, Берлова, Баха.

А. Астров.