Звук

Звук. Необходимо отличать два понятия о звуке. Звук, как явление субъективное, или физиологическое, есть определенного рода ощущение, которое воспринимается органом слуха и вызывается колебанием материи, распространяющимся до этого органа. Звук, как явление объективное, или физическое, и заключается в этих распространяющихся колебаниях. Существуют колебания, которые не воспринимаются органом слуха, а между тем никакими особенными свойствами не отличаются от колебаний, действующих на этот орган. В этом случае приходится ввести понятие о неслышимых звуках. Причина отсутствия физиологического действия может заключаться или в чрезмерной слабости звука или в слишком большом или малом числе колебаний. Один и тот же звук может восприниматься органом слуха одних лиц и вовсе не восприниматься органом слуха других. Для последних физиологического явления звука вовсе не существует. Для получения «неслышимых звуков» весьма удобен свисток Гальтона, звук которого можно повышать до пределов, когда они перестают восприниматься органом слуха.  Учение о звуке, как о физическом явлении называется акустикой. Этот отдел физики отличается от других отделов отсутствием каких-либо специальных гипотез, играющих более или менее существенную роль. Основная сущность звуковых явлений, а именно, колебательные движения материи, во многих случаях непосредственно заметна. Теоретическая акустика есть отдел учения об упругости, трактующий о распространении колебательных движений в упругой среде. Физиологическая акустика рассматривает устройство органов слуха и способа восприятия ими звуковых колебаний. Кроме того, и орган речи, как источник звука, представляет интерес для акустики. Особенность акустики заключается еще в том, что она тесно соприкасается с наиболее между людьми распространенным искусством — музыкой. Источниками звука могут служить твердые, жидкие или газообразные тела, каким-либо способом приведенные в достаточно быстрое колебательное движение. Если данное тело колеблется, как целое, то оно может совершать лишь одно определенное число колебаний в секунду; это число зависит от геометрической формы, от химического состава тела и от его физического состояния (например, от температуры). Оказывается, однако, что тело может, как бы разделиться на части, которые колеблются отдельно; в этом случае числа колебаний в секунду уже получаются другие. Кроме того, в некоторых случаях число колебаний для данного тела зависит от их направления. Так, например, поперечные и продольные колебания стержня, один из концов которого закреплен, происходят с весьма различной скоростью. Звучащие тела вызывают в окружающем воздухе продольные колебания, распространяющиеся лучеобразно во все стороны. Вдоль звукового луча чередуются сгущения и разрежения, которые как бы скользят вдоль луча с некоторой скоростью, называемой скоростью звука. Расстояние центров двух соседних сгущений или разрежений есть длина волны λ; она связана со скоростью звука V, временем колебания Т и числом N колебаний в секунду уравнениями: λ = VТ и V = Nλ. Возможность физиологического впечатления зависит от числа N, которое не должно быть меньше некоторого числа (около 16) и не больше некоторого другого, весьма неодинакового для различных лиц (в среднем, около 25 000). Звуковые колебания распространяются в твердых, жидких и газообразных средах. Скорость звука зависит от рода среды и от ее физического состояния. Задача о законах колебаний звучащих тел может быть сведена к задаче о распространении колебательных движений в этих телах, ибо самое колебание тела можно рассматривать как результат интерференции колебаний, распространяющихся внутри тела и отражающихся от его пределов. При такой интерференции образуются стоячие волны (см. колебательное движение) с пучностями и узлами. Колебания тел и могут быть рассматриваемы как частные случаи стоячих волн.

Звуки  разделяются на простые, или музыкальные, тоны и на звуки сложные. Простой звук, который называется еще чистым, получается, когда звучащее тело совершает строго гармоническое колебательное движение. Сложный звук состоит из сочетания простых тонов. Музыкальные тоны, или звуки, отличаются друг от друга по силе и высоте. Сила звука определяется энергией колебательного движения, которое пропорционально квадрату амплитуды (см. колебательное движение), если сравнивать звуки одинаковой высоты, распространяющиеся в одной и той же среде. Если сравнивать различные среды, то оказывается, что физиологическая сила звука данной высоты пропорциональна скорости звука, плотности среды и квадрату амплитуды. Высота простого звука есть понятие, не поддающееся определению; оно непосредственно получается при сравнении впечатлений от двух различных тонов. Высота тона зависит от числа колебаний N. Если от тона, число колебаний которого N, переходить к тонам все более и более высоким, то, наконец, встречается тон, особенно близкий к первому и с ним наиболее сливающийся. Он называется октавой первого тона, и оказывается, что его число колебаний равно 2N. Между данным тоном и его октавой помещается ряд промежуточных тонов, составляющих простейшую гамму (см.). Названия и число колебаний этих тонов, если начинать с основного звука ut, следующие: ut (N), re (⁹/₈N), mi (⁵/₄N), fa (⁴/₃N), sol (²/₃N), la (⁵/₈N), si (¹⁵/₈N), ut (2N). В Германии и Англии, а отчасти и у нас употребляют и другое обозначение тонов: с, d, е, f, g, а, h, с. Тон si, или h, в Англии обозначается через b; тон ut иногда называется еще do. Чтобы отличить последовательные октавы друг от друга, приставляют к названию тона числа или черточки сбоку или сверху или вводят большие буквы. За нормальный тон, относительно которого настраивают музыкальные инструменты, принимают lа₃ (между второй и третьей линиями в скрипичном ключе). Этот тон должен иметь N=435 колебаний. Если ut принять за основной тон, то re составляет его секунду, mi — терцию (большую), fa — кварту, sol — квинту, Іа — сексту, si — септиму; следующий ut составляет октаву, и т. д. Следующее затем sol есть дуодецима. Кроме перечисленных выше тонов, применяются еще тона промежуточные, обозначаемые диезами и бемолями. Тона одинаково высокие, издаваемые различными музыкальными инструментами или  при пении различными лицами или, наконец, одним лицом, поющим данный тон на различные гласные буквы, отличаются друг от друга оттенком, или тембром. Это отличие есть следствие сложности звуков, которые состоят из основного тона и целого ряда добавочных тонов. Происходит это оттого, что к колебаниям тела как целого примешиваются колебания отдельных его частей, на которые оно как бы распадается. Так, например, при колебаниях струны она как целое дает основной тон; но вместе с тем колеблется каждая ее половина отдельно, причем получается октава основного тона; далее, струна разделяется на три части, из которых каждая дает кварту следующей октавы (3N колебаний); каждая ¼  струны совершает 4N, каждая 1/5  часть — 5N колебаний, и т. д. Число, высота и сила добавочных тонов могут быть бесконечно разнообразны, вследствие чего и оттенки, которые они придают основному тону, могут быть бесконечно различны. Присутствие добавочных тонов меняет закон колебательного движения, которое перестает быть простым гармоническим. Итак, оттенок звука зависит от формы колебательного движения. Если число добавочных тонов весьма велико, то получается явление шума. Впрочем, и во всяком шуме существуют отдельные, как бы особенно рельефно выступающие, тона. Сила звука меняется обратно пропорционально квадрату расстояния от звучащего тела, если распространение звука происходит в неограниченной среде. При распространении звука внутри трубы происходит очень медленная потеря звуковой энергии, вследствие чего сила звука передается через трубу на большое расстояние, ослабевая при этом весьма медленно.

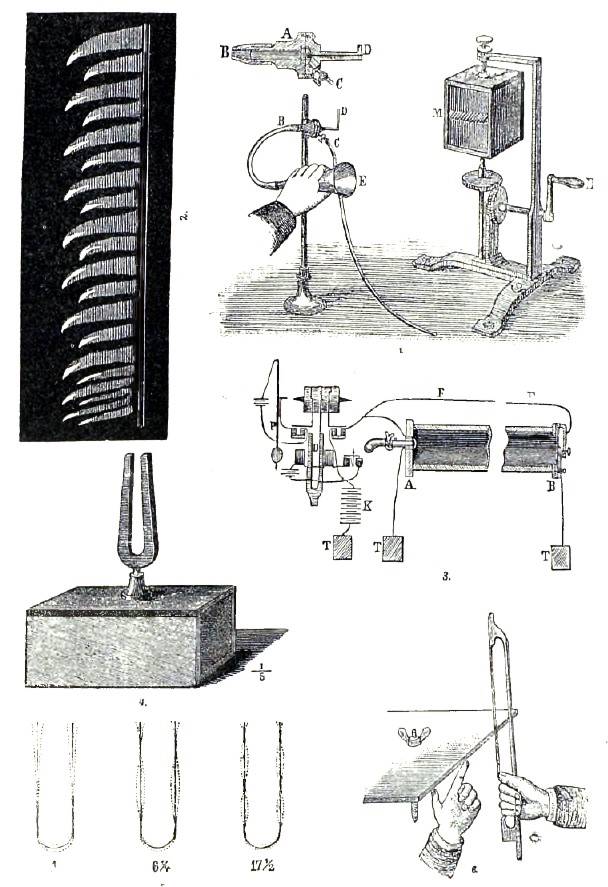
При исследовании звуковых явлений могут быть весьма полезны манометрическое пламя и чувствительное пламя. Первое из них получается следующим образом: небольшая камера А (рис. 1) разделена упругой перепонкой на две части, или камеры; в одну из частей вставлена трубка С, через которую проникает светильный газ, и вторая трубка, оканчивающаяся горелкой D. В другую часть проникает через ЕВ исследуемый звук, который заставляет упругую перепонку колебаться. Эти колебания передаются через светильный газ самому пламени, которое подвергается N удлинениям и укорачиваниям в секунду, где N имеет прежнее значение. Если наблюдать изображение пламени в быстро вращающемся зеркале М, то огненная полоса, видимая в зеркале, разделяется на части различной длины, как бы зазубривается, причем форма зазубрин усложняется, если исследуемый звук не простой. На рис. 2 показан вид этих зазубрин в одном частном случае. Чувствительное пламя получается, если зажечь струю газа, выходящего из малого отверстия под большим давлением. При этом получается длинное тонкое пламя, весьма чувствительное к высоким звукам, под влиянием которых оно укорачивается, утолщается и делается шипящим. Скорость V звука в газах определяется формулой Лапласа V = √(pgk)/D, в которой D — вес единицы объема газа, р — упругость газа, g — ускорение силы тяжести и k — отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме (см. газы, XII, 313). Чтобы получить V в метрах в секунду, следует р выразить, например, в килограммах на кв. метр поверхности (р=10 333, если давление равно одной атмосфере), D — в килограммах на куб. метр, наконец, следует положить g=9,81. Для воздуха и некоторых других газов, весьма далеких от насыщения, k=1,4. Формула Лапласа дает для воздуха при 0° скорость V=332,4 метра в секунду. Из формулы Лапласа вытекают такие следствия: скорость звука в сухом газе не зависит от его упругости; скорость звука в газах пропорциональна корню квадратному из абсолютной температуры. При одинаковых температурах скорости звука в различных газах, имеющих одинаковое k, обратно пропорциональны корням квадратным из их плотностей, взятых относительно воздуха, находящегося при одинаковых с ними температуре и давлении. Скорость звука в водороде в 3,8 раз больше скорости в воздухе. Скорость звука определялась до Реньо по способу измерения времени, истекающего от момента, когда наблюдатель замечает световую вспышку при выстреле, произведенном ночью на возможно большем от него расстоянии, до момента, когда наблюдатель слышит звук выстрела. Зная расстояние от наблюдателя до того места, где производится выстрел, легко вычислить скорость звука, на которую при этих опытах должны иметь влияние скорость и направление ветра. Первое определение скорости звука принадлежит Мерсенню (1640 г.; Mersenne V=448 м). Затем, члены итальянской академии Del Cimento нашли в 1656 г. V=361 м, Бойль в 1700 г. V=351 м, и т. д. В 1738 г. члены французской академии производили определение V в окрестностях Парнаса; они нашли при 0° скорость звука = 332 м. Из многих дальнейших определений представляют особый интерес знаменитые определения, произведенные ночью с 21 на 22 июня 1822 г. около Парижа двумя комиссиями, находившимися на расстоянии 18 622 м друг от друга. В состав этих комиссий вошли: Арого, Прони, Гей-Люссак, Гумбольдт и др. Они нашли V=330,8 м при 0°. В 1821 г. Moll и Ван-Деек производили определение около Амстердама и нашли (при 0°) V=332,05 м. Некоторые поправки, которые впоследствии были введены в их вычисления, дали V=332,77 м. Наблюдения, произведенные в Швейцарии на различных высотах, а также в 1825 г. во время экспедиции Франклина при температуре —40° дали результаты, согласные с теоретическими формулами. В 1862—66 г. Реньо (Regnault) определял скорость звука в газо- и водопроводных трубах, которые в то время были проложены под Парижем. Распределение частей прибора изображено на рис. Звук. Конец А трубы АВ закрыт пластинкой, снабженной отверстием, через которое проходило дуло пистолета; другой конец В трубы был затянут упругой перепонкой, посреди которой помещалась небольшая металлическая пластинка, соединенная с землей Т. Батарея К соединена с землей Т и с небольшим электромагнитом, пройдя который ток разветвлялся на две ветви. Одна ветвь FF была соединена со штифтом, острие которого находилось вблизи упомянутой металлической пластинки; другая ветвь была проведена мимо дула пистолета и соединена с землей Т. Три рядом расположенных штифта касались поверхности равномерно вращающегося цилиндра, покрытого листом вычерненной бумаги. Крайний, с правой стороны, штифт был соединен с якорем упомянутого электромагнита, находившегося под действием батареи К; средний штифт чертил волнообразную линию под влиянием звучащего камертона D и, наконец, третий штифт отмечал на поверхности цилиндра секунды под влиянием секундного маятника Р. Ток батареи К замкнут; он проходит мимо дула пистолета; другая ветвь разомкнута в В между штифтом и пластинкой. В момент выстрела разрывается проволока перед дулом пистолета, электромагнит перестает действовать на якорь, и правый штифт перемещается в сторону. Когда звуковое сотрясение достигает другого конца трубы, то упругая перепонка выпучивается наружу, вследствие чего пластинка касается штифта. В этот момент происходит замыкание ответвления FF, и электромагнит заставляет правый штифтик уклониться в сторону. Таким образом, отмечаются на цилиндре начало и конец времени, в течение которого звук проходит всю длину трубы. Продолжительность этого времени определяется числом зигзагов, начертанных средним штифтиком, причем число зигзагов, происходящих в секунду, определяется левым штифтиком. Реньо вывел из своих наблюдений, что скорость звука несколько возрастает с его силой и что она тем меньше, чем меньше диаметр трубы. Далее, Реньо нашел, что скорость высоких звуков меньше скорости звуков низких; однако, он сам сомневался в точности этого результата. Для толстых труб Реньо нашел при 0° V=330,6 м; опыты на свободном воздухе дали ему V= 330,7 м. При +20° скорость звука в воздухе равна 342,5 м в секунду. Скорость звука в жидкостях V = √(10333g/kD), в которой g — ускорение силы тяжести, D — вес куб. метра жидкости в килограммах и k — коэффициент сжатия жидкости, отнесенный к давлению в одну атмосферу (относительное уменьшение объема жидкости, когда внешнее давление увеличивается на одну атмосферу). Для воды D = 1000, k = 0,00005. Это дает для воды V = 1424 м. Опыты Штурма и Кульдена (Sturm et Colladon) в 1827 г. на Женевском озере дали при 8,1° скорость V = 1435 м. Скорость звука в твердых стержнях или проволоках определяется формулой V = √(Eg/1000δ) в которой g — ускорение силы тяжести (9,81), δ — плотность вещества относительно воды, Е — модуль Юнга, отнесенный к 1 кв. метру площади поперечного сечения. Этот модуль в 10⁶ раз больше модуля, обыкновенно помещаемого в таблицах и отнесенного к одному кв. мм  площади поперечного сечения. Для стали δ = 7,7 и Е = 20000∙10⁶; эти числа дают для стали V = 5048 м. Скорость V₁ звука в неограниченной твердой среде выражается более сложной формулой, в которую входит коэффициент  σ Пуассона (отношение поперечного сжатия к продольному удлинению при растяжении); скорость V₁ всегда больше V. Интересно, что скорости звука в водороде (1280 м), в воде (1450 м) и в свинце (1450 м) не очень отличаются друг от друга. Различные вещества не одинаково хорошо передают звук, т. е. обладают неодинаковой звукопроводностью. Этим вопросом занимался в особенности Н. А. Гезехус (в Петербурге). Он отвинчивал камертон от резонаторного ящика, ставил на ящик вертикальный стержень из испытуемого материала, а на него ножку звучащего камертона. По силе звука, издаваемого ящиком, можно было судить о звукопроводности материала. Таким образом, получается ряд тел с возрастающей звукопроводностью: каучук, пробка, дерево, стекло, сталь. Дерево лучше проводит звук вдоль, чем поперек волокон. Большое значение имеет вопрос  о звукопроводности воздуха, например, при передаче звуковых сигналов, особенно для мореплавания. Тиндаль нашел, что звукопроводность воздуха чрезвычайно уменьшена, когда он состоит из вертикальных столбов различной температуры, как это бывает в летние солнечные дни, когда, в зависимости от нагревания почвы, поднимаются отдельные столбы теплого воздуха, отделенные друг от друга столбами более холодными. На границах между ними происходит отражение звука. Произведя искусственно, при помощи горелок, ряды восходящих потоков теплого воздуха, Тиндаль мог на опыте доказать, что такие слои сильно отражают, но очень мало пропускают звук. Отражение и преломление звука происходят по тем же законам, как отражение и преломление света. На отражении звука основано явление «эхо» и то, что называется «акустикой» больших зал, например, концертных, театров, церквей и т. д. Этим вопросом занимались Sabine (1900, 1906) и Marage (1906, 1907). Первый показал, что звук, достигающий слушателя в закрытом помещении, состоит из трех частей: 1) звук, непосредственно идущий от источника (оратор, певец, музыкальный инструмент и т. д.); 2) звук, правильно отраженный от стен, и 3) звук, рассеянный различными предметами (занавесы, мягкая мебель) и людьми. Для того, чтобы акустика помещения была хорошая, должна вполне отсутствовать вторая часть, а третья (резонанс) должна в небольших помещениях продолжаться около 1 сек., а в обширных от 1 до 2 сек.; если она менее или более продолжительна, то акустика плохая. Sabine дает для продолжительности Т резонанса формулу Т=kV: (а+с), где V — объем помещения, а — поглощение стенами, с — поглощение людьми, причем за единицу принято поглощение, вызванное открытым окном в 1 кв. м поверхности; с = nb, где n число людей и b = 0,44. Величина k = 0, 171; Wallace находит k = 0,164. Marage находит, что Т должно находиться между 0,5 и 1 сек. Замечательный по своей акустике зал находится в Salt Lake City (Америка, зал собраний мормонов); его ширина 50 м, длина 83 м, высота 27 м; он вмещает 7 500 человек, и, даже когда он вполне наполнен, можно во всех его частях  услышать падение булавки на стол, стоящий перед оратором.

Преломление звука исследовали Н. А. Гезехус, Hajech и многие другие ученые. П. П. Кастерин (Одесса) первый исследовал теоретически и экспериментально явление звуковой дисперсии и мог даже обнаружить существование аномальной дисперсии около тех звуков, которые данной средой поглощаются. Звуки  способны интерферировать (см. колебательное движение) и образовать стоячие волны с пучностями и узлами. Лорд Рэлей (Rayleigh) произвел ряд опытов, обнаруживающих явление звуковой дифракции.

В музыке пользуются, между прочим, звучащими струнами и звучащими столбами воздуха в трубах (духовые инструменты). Законы колебания струн открыл Мерсеннь (Mersenne) в 1636 г. Число колебаний N струны обратно пропорционально ее длине, обратно пропорционально ее толщине, или радиусу ее поперечного сечения, обратно пропорционально корню квадратному из ее плотности и прямо пропорционально корню квадратному из ее натяжения (измеряемого грузом, который можно себе представить привешенным к одному из ее концов). Из указанных законов вытекает такое следствие: число колебаний струны при данной длине и данном натяжении обратно пропорционально корню квадратному из ее массы. Колебания струны можно рассматривать, как пример стоячей волны, причем на двух концах непременно находятся узлы, а на самой струне, по крайней мере, одна пучность. Но между концами струны может образоваться еще произвольное число узлов, причем число пучностей на единицу больше числа этих узлов. Форма колебаний различных точек струны может быть в высшей степени различна; она зависит от способа приведения струны в колебание и от относительного положения точки рассматриваемой и точки, в которой действуют на струну ударом (рояль), пальцем (арфа), смычком, крючком или иным способом. Приведенные выше законы относятся к струнам абсолютно мягким и не упругим, колебание которых вызывается только натяжением. Для твердых и упругих струн получаются более сложные законы колебания. В струне могут образоваться также и продольные колебания, причем получается гораздо более высокий звук, чем при колебаниях поперечных, даже при очень сильном натяжении струны. Число N₁ продольных колебаний и число N поперечных колебаний связаны формулой: N: N₁ = √ΔL:L, в которой L — длина струны, а ΔL — то удлинение, которое вызвано ее натяжением, когда она дает N поперечных колебаний. Эта формула ясно показывает, что N₁ всегда гораздо больше N. Стержни, скрепленные на одном из концов или на обоих концах, также могут совершать поперечные и продольные колебания, причем как те, так и другие вызываются исключительно внутренними упругими силами. Пример звучащего стержня представляет камертон (рис. 4), способный дать различные звуки, соответствующие различным формам колебаний, показанным на рис. 5. В первом случае получается основной тон (число колебаний N), и каждая ветвь камертона колеблется как целое; во втором случае образуется по одной пучности и одному узлу на каждой ветви, кроме пучности, находящейся на конце (число колебаний 6 ¼  N). Еще более сложное колебание камертона изображено на третьем рисунке: для него число колебаний 17½N. Упругие пластинки способны к весьма сложным колебаниям. Если стеклянную или металлическую пластинку закрепить в горизонтальном положении (рис. 6), вдоль края ее провести смычком и в то же время некоторых точек края касаться пальцами, то вся пластинка как бы разделяется на части, середины которых находятся в наиболее быстрых движениях (пучности). Эти части отделены друг от друга узловыми линиями, в которых частицы остаются в покое. Если на такую пластинку насыпать песок, то последний сбрасывается с пучности и собирается вдоль узловых линий, образуя разного рода более или менее правильные фигуры, зависящие от формы, толщины и от материала пластинок и от тех точек, в которых пластинка закреплена, которых касаемся пальцами и около которых проводим смычком. Эти фигуры называются Хладниевыми. Одна из них изображена на рис. 7; смычком проведено около b, точек аа касались пальцами.  

Воздух или иной газ, находящийся в трубе, может быть приведен в колебательное движение (звучащие трубы). На одном конце трубы производится сотрясение воздуха, и в этом месте, во всяком случае, находится пучность; другой конец трубы может быть открытый или закрытый. В открытой трубе находятся пучность около отверстия и, по крайней мере, один узел внутри трубы. В пучностях частицы воздуха движутся с наибольшей амплитудой, но зато плотность воздуха почти постоянная. В узлах частицы находятся в покое, но зато плотность воздуха подвергается наибольшим изменениям, так как движение частиц, находящихся с двух сторон от узла, имеет противоположное направление. Вследствие этого образуется в узлах попеременно сгущение и разрежение воздуха. Так как расстояние двух ближайших пучностей равно полуволне, то длина волны основного тона в открытой трубе равна удвоенной длине самой трубы. Кроме основного тона, открытая труба может дать еще ряд других более высоких, которым соответствуют два, три и т. д. узла внутри трубы и соответствующие пучности между ними. Числа колебаний различных тонов открытой трубы определяются формулой: N_n = 2nV/4L где n — целое число, L — длина трубы; n = 1 соответствует основному тону. В закрытой трубе должен находиться узел у закрытого конца, а так как на другом конце находится пучность, то в простейшем случае внутри трубы вовсе не образуются ни узлы, ни пучности. При этом получается основной тон закрытой трубы, и ее длина L равна ¼  длины волны этого тона. Таким образом, для основного тона длина волны в 4 раза превышает длину трубы, а отсюда следует, что при равной длине основной тон закрытой трубы на одну октаву ниже основного тона трубы открытой. Кроме основного тона, закрытая труба может дать и ряд других, причем внутри трубы образуется один, два и т. д. узла, а между узлами — соответствующие пучности. Число колебаний различных звуков, даваемых закрытой трубой, определяется формулой: N_n = (2n + 1)V/4L. Из сказанного следует, что если N — число колебаний основного тона закрытой трубы, то числа колебаний остальных тонов той же трубы равны 3N, 5N, 7N и т. д., а числа колебаний тонов открытой трубы той же длины: 2N, 4N, 6N, 8N и т. д. На рис. 8 изображена в разрезе органная труба. Расстояние RR представляет длину трубы, которая считается от верхней поверхности призмы cd, не доходящей до противоположной стенки, так что образуется щель. Воздух, выдуваемый в нижнюю трубку, вступает в камеру К и выходит через упомянутую щель; здесь он ударяется об острое ребро ab клина, вырезанного в боковой стенке трубы. В этом месте происходит сгущение воздуха, которое распространяется вдоль столба воздуха, находящегося в трубе. Это сгущение заставляет дальнейший поток воздуха выходить через боковую щель, а не вовнутрь трубы, вследствие чего самое сгущение воздуха расширяется, и на его месте образуется разрежение, которое также распространяется вдоль трубы. Новая струя воздуха опять вызывает сгущение и т. д. В результате получается неправильное сотрясение воздуха или шум, т. е. большое число различных тонов, из которых труба как бы выбирает тон, соответствующий ее длине и способный образовать в ней стоячие волны. Этот тон чрезвычайно усиливается трубой и заглушает все остальные, хотя легкий шум все-таки остается заметным. Существует целый ряд способов для наблюдения пучностей и узлов внутри звучащих труб. Формулы, которые мы привели выше для числа колебаний тонов  открытых и закрытых труб, не вполне точны. Действительно, наблюдаемые числа колебаний несколько меньше тех, которые определяются элементарными формулами. Это объясняется, во-1-х, влиянием плоской стороны призмы cd, от которой отражаются колебания, образующие стоячие волны. Кроме того, в открытых трубах пучности находятся вне трубы и на некотором расстоянии от ее отверстия. Кундт дал весьма важный способ определения скорости звука в газообразных, жидких и твердых телах при помощи звучащих труб. Этот способ заключается в следующем (рис. 9). Стеклянная трубка АВ располагается горизонтально; на конце А находится пробка, которую можно при помощи крючка немного перемещать. С другой стороны входит в трубку металлический или стеклянный стержень CD, зажатый в Е посредине и оканчивающийся у С небольшим диском. В трубке распределяют равномерно какой-либо сухой порошок. Если путем продольного натирания привести половину ED в продольные колебания, то такие же колебания совершит и другая половина СЕ. Эти колебания, распространяясь от С к А, отразятся здесь и образуют систему стоячих волн. При этом порошок разбрасывается в пучностях и собирается в узлах nnn... Перемещая немного пробку А, можно добиться того, что около А и С образуются узлы, а это способствует собиранию порошка в резко очерченные кучки NNN... Боковые трубки, не изображенные на рисунке, дают возможность наполнять трубку испытуемым газом. Скорости звука в различных газах, наполняющих трубку, относятся между собой как расстояния этих кучек друг от друга. Наполняя трубку различными жидкостями, можно сравнить между собой скорости звука в этих жидкостях, а также сравнить их со скоростями звука в различных газах. Способ Кундта дает возможность определить скорость звука и в твердых телах, если из них приготовить стержень CD, при колебаниях которого в Е образуется узел, а на концах С и D — пучности. Отсюда следует, что длина CD всего стержня равна полуволне, а так как расстояние двух кучек также равно полуволне, то ясно, что скорость звука в твердом теле CD относится к скорости звука в газе, наполняющем трубку, как длина стержня относится к расстоянию соседних кучек.

Вертикальная труба, внутри которой горит небольшое пламя водорода или светильного газа (рис. 10), звучит, издавая один из тонов, соответствующих длине трубы. Это — так называемое поющее пламя, или газовая гармоника. Рике (Rijke) показал, что, если внутри широкой трубы поместить поперечную металлическую сетку, нагреть ее пламенем газовой горелки и затем пламя убрать, то труба сильно звучит, пока сетка не охладится. Этот способ усовершенствовал Пфлаум (в Риге), заменивший сетку платиновой зигзаговидной проволокой, которая нагревается электрическим током. Высота тона, даваемая язычковой трубой, находится в сложной зависимости от числа колебаний язычка и от длины трубы.  Для определения чисел колебаний, соответствующих данному тону, служит, между прочим, сирена Каньяр де Латура; она изображена на рис. 11; ее главнейшие части следующие: круглая коробка АА, в которую снизу через трубку ВВ вдувается воздух; сверху коробка покрыта неподвижной крышкой, над которой помещен круг SS, вращающийся около вертикальной оси d. На верхнем чертеже виден этот круг сверху; на нижнем представлена коробка, часть которой срезана вертикальной плоскостью, проходящей по линии nn верхнего чертежа. Крышка коробки АА и подвижной круг снабжены рядом каналов, расположенных по окружности и наклоненных друг к другу так, как это показано на нижнем рисунке. Когда верхний круг вращается, то при каждом его обороте n раз откроются все каналы, где n число каналов в каждом из двух кругов. В эти моменты вырываются струи сжатого воздуха из коробки АА наружу, производя над кругом SS сжатие воздуха, которое в следующий момент, когда все каналы закроются, превратится в разрежение; при следующем открывании отверстий получается опять сжатие, и т. д. Если круг SS совершает в одну секунду k оборотов, то получается звук, число колебаний которого N = nk. Вращение круга ускоряется и поддерживается струями воздуха, проходящими через каналы и производящими боковые давления на стенки каналов вращающегося круга. Для определения числа k оборотов SS служит счетчик, приводимый в движение бесконечным винтом, вырезанным на поверхности оси d. Желая определить число колебаний данного тона, стараются регулировать приток воздуха в сирену так, чтобы издаваемый ею тон был тождествен с тем, число колебаний которого нужно определить. Определив при помощи счетчика число k, мы легко найдем искомое число N. Число колебаний камертона может быть определено, если к одной из его ветвей прикрепить острие r (рис. 12), которое чертило бы волновую линию на поверхности вращающегося цилиндра Т. Рядом с камертоном помещают другое острие S, отмечающее при помощи секундного маятника отдельные секунды. Остается сосчитать число зигзагов, начертанных камертоном, между двумя знаками, отмеченными вторым острием. Липпманн дал весьма остроумный способ сравнения числа колебаний двух камертонов. Если какое-нибудь тело помещено в среде, в которой распространяются и до него доходят колебания, быстрота которых равна быстроте возможных колебаний самого тела, то это последнее само начинает колебаться. Всякое тело поглощает те колебания, которые оно само способно совершать или, иначе, которые оно способно испускать. На этом основано весьма важное явление акустического резонанса. Так, например, струна, камертон и т. д. начинают колебаться и звучать, когда до них доходит тот самый тон, который они способны издавать. То же самое относится к столбам воздуха, находящимся внутри цилиндрического, шаровидного или иной формы сосуда. На этом основаны резонаторы, цилиндрические или шаровидные сосуды с круглым отверстием а (рис. 13); они начинают звучать, если до них доходит звук, соответствующий их геометрической форме и их размерам. Камертоны ставятся поэтому на резонаторные ящики (см. рис. 4), длина которых равна ¼  длины волны основного звука камертона. На этом же основано применение резонаторов для анализа сложного звука, т. е. для определения присутствия в нем того или другого тона. На рис. 14 изображен прибор Кенига, служащий для анализа звука; он состоит из ряда шаровых резонаторов, распределенных один над другим; на рисунке видны круглые отверстия резонаторов. Задняя стенка каждого из этих резонаторов соединена при помощи каучуковой трубки с одной из камер, в которых колебания передаются манометрическим пламенем (см. выше). Эти манометрические пламени рассматриваются в системе зеркал, приводимых во вращение при помощи рукоятки и зубчатых колес. Если в звуке, доходящем до этого прибора, заключается тон, соответствующий одному из резонаторов, то на огненной полосе в зеркале замечаются зазубрины (рис. 2).  Если наблюдатель и источник звука не перемещаются, то число колебаний, доходящих в одну секунду до наблюдателя, равно числу колебаний, производимых в одну секунду источником звука. Наблюдатель слышит тот тон, который издается источником звука. Но если наблюдатель и источник приближаются друг к другу, то число колебаний, доходящих в единицу времени до наблюдателя, будет больше числа колебаний, производимых в то же время источниками; наоборот, первое число меньше второго, если наблюдатель и источник друг от друга удалятся. Это — так называемый принцип Допплера (Doppler), прилагающийся также к явлениям световым. Из сказанного следует, что, если источник и наблюдатель приближаются друг к другу, то наблюдатель слышит звук, который выше, а когда они удаляются друг от друга, то он слышит звук, который ниже того звука, который замечается при неподвижности источника и наблюдателя. Это явление легко наблюдается, например, когда локомотив, свисток которого находится в действии, быстро проезжает мимо наблюдателя, — в этот момент замечается ясное понижение тона. Если одновременно производятся два тона, числа колебаний которых N и N + n, где n мало сравнительно с N, то наблюдатель замечает попеременное усиление и ослабление силы звука; это — так называемые биения. Число биений в одну секунду равняется разности n числа колебаний двух тонов. Наблюдая биения, можно сравнить числа колебаний двух камертонов, настроенных почти на один и тот же тон. На этом основаны приборы, устроенные, между прочим, отцом Аристархом Израэлевым, Шейблером и др.  При одновременном звучании двух тел, числа колебаний которых N и N₁, слышится новый тон, более низкий; его число колебаний n равно N₁—N. Этот тон называется разностным; его открыли приблизительно одновременно Зорге в Гамбурге (1744 г.), Ромье (Romier) в Монпелье (1753 г.) и Тартини в Падуе (1757 г.). Нетрудно наблюдать разностный тон при одновременном звучании двух камертонов, особенно если сперва заставить звучать третий камертон, который дает ожидаемый разностный тон. Гельмгольц построил двойную сирену, которая особенно удобна для наблюдения разностных тонов. Гельмгольц открыл существование суммовых тонов, число колебаний которых равно n = N + N₁. Разностные и суммовые тоны называются еще комбинационными. Вопрос о происхождении разностных и суммовых тонов до сих пор нельзя считать окончательно решенным. Лагранж (1795 г.) и Юнг (1800 г.) полагали, что разностный тон происходит от биений, число которых, как было сказано выше, тоже равняется разности чисел колебаний двух одновременных тонов. Биения, достаточно частые, производят по их теории впечатление отдельного тона. Гельмгольц дал другую теорию происхождения комбинационных тонов вообще. Разбирая теоретически звуковые явления, предполагают, что простому тону соответствуют гармонические колебательные движения, т. е., что сила, действующая на колеблющуюся частицу, пропорциональна ее расстоянию от положения равновесия (см. колебательное движение). Гельмгольц допустил, что при достаточно сильных колебаниях следует предположить, что выражение силы состоит из двух частей, из которых одна пропорциональна первой степени, а вторая пропорциональна квадрату удаления частицы от положения равновесия. Допуская такой закон действующих сил, Гельмгольц теоретически вывел, что при одновременном возбуждении тонов, числа колебаний которых — N и N₁; должны реально образоваться еще тоны, числа колебаний которых: 1) 2N, 2N₁; 3N, 3N₁, 2) N₁ — N, N₁ + N, 3) 2N + N₁; 2N—N₁, 2N₁ + N, 2N₁ — N. Между этими тонами находятся и комбинационные тоны. Добавочные тоны, примешанные к данным звукам, также могут образовать между собой биения. Для записи колебаний, соответствующих сложному звуку, служит, между прочим, фонаутограф Скотта. Фонограф (см.) Эдисона не только записывает сложные колебания, но и может обратно превратить их в соответствующие звуки. Звук  человеческого голоса содержит весьма большое число добавочных тонов; их высота и расположение зависят от формы и объема, которые принимает полость рта при произношении звуков. От этих добавочных тонов зависит оттенок голоса, определяющий особенность голосов различных лиц, а также голос одного и того же лица при произношении различных гласных букв. Гельмгольцу удалось определить добавочные тоны, соответствующие отдельным гласным и служащие для их характеристики, т. е. произвести анализ гласных. Далее, Гельмгольц построил прибор, при помощи которого ему удалось произвести синтез гласных, заставляя одновременно звучать ряд камертонов, дававших те тоны,  которые входят в состав гласной.

Литература: Столетов, «Введение в акустику и оптику», Москва (1895); Слугинов, «Акустика», Казань (1891); Melde, «Akustik», Leipzig (1883); Zellner, «Vorträge über Akustik», Leipzig (1892); Lord Rayleigh, «Theory of Sound», London (1877); Helmholtz, «Die Lehre von den Tonempfindungen» (1870); Violle, «Cours de phys.», т. II, partie 1, Paris (1888); Kalaehne, «Mathem.-physikalische Akustik», Leipzig (1910); Waetzmann, «Resonanztheorie des Hörens», Braunschweig (1912).

О. Хвольсон.