Жидкости

Жидкости. Подобно газам, жидкости не имеют самостоятельной формы, но принимают форму сосуда, в котором они находятся. Они весьма мало сопротивляются изменению формы, т. е. деформациям. Но жидкости отличаются от газов, между прочим, тем, что обладают определенным объемом и весьма сильно сопротивляются его изменению. Жидкая масса, не подверженная внешним силам и не вращающаяся, принимает форму шара, которая и должна считаться за естественную ее форму. Жидкости  при всех условиях испаряются, т. е. переходят в газообразное состояние. Этот переход сопровождается затратой энергии, которая в паре находится в потенциальной форме. Жидкость называется идеальной, или совершенной, если она вовсе не сопротивляется изменению формы, абсолютно несжимаема и абсолютно подвижна, т. е. не обладает внутренним трением или вязкостью.

Учение о жидкостях, находящихся в состоянии покоя, называется гидростатикой. Она основывается, прежде всего, на законе Паскаля, который определяет влияние давления, производимого на поверхность жидкости. Закон Паскаля говорит, что всякое давление передается жидкости равномерно во все стороны. Это означает, что если на единицу поверхности жидкости производится внешними силами некоторое давление р, то жидкость производит такое же давление р на каждую единицу поверхности стенок окружающего ее сосуда. Отсюда следует, что жидкость, не подверженная никаким силам, кроме давлений на ее поверхность, может быть в равновесии только в том случае, когда вся ее поверхность подвержена везде одинаковому давлению. На законе Паскаля основано устройство гидравлического пресса (см.). Под влиянием силы тяжести возникает давление горизонтальных слоев жидкости друг на друга и давление жидкости на дно и стенки сосуда, причем к последним следует отнести также и поверхность всякого погруженного в жидкость тела. Это давление жидкости называется гидростатическим давлением. Для равновесия жидкости, находящейся под влиянием силы тяжести, необходимо, чтобы все части поверхности горизонтального слоя жидкости находились под одинаковым давлением, которое равно давлению этого же слоя на боковые стенки сосуда. Отсюда вытекает ряд следствий. Свободная поверхность жидкости должна, при равновесии, составлять горизонтальную плоскость. Однородная жидкость должна в сообщающихся сосудах стоять на одинаковой высоте, т. е. свободные поверхности жидкости должны во всех сосудах лежать в одной горизонтальной плоскости. Высоты столбов различных жидкостей, помещенных в сообщающихся сосудах, обратно пропорциональны плотностям этих жидкостей. Давление жидкости на горизонтальное дно сосуда равно весу вертикального столба жидкости, площадь поперечного сечения которого равна площади дна, а высота равна вертикальному расстоянию дна сосуда от поверхности жидкости. Давление жидкости на весьма малую часть s поверхности боковой стенки сосуда равно весу вертикального столба жидкости, площадь поперечного сечения которого равна s, а высота равна вертикальному расстоянию от s до свободной поверхности жидкости. Отсюда следует, что давление жидкости на дно сосуда не зависит от формы сосуда, т. е. от вида его боковых стенок. Равнодействующая всех давлений жидкости на плоскую стенку сосуда приложена к центру тяжести геометрической фигуры той части стенки, которая касается жидкости. Вся поверхность тела, погруженного в жидкость, подвергается гидростатическому ее давлению, которое —тем больше, чем дальше она находится от поверхности жидкости. Давление на тело снизу должно поэтому быть больше давления сверху. Равнодействующая всех давлений направлена вертикально вверх, вследствие чего тело, погруженное в жидкость, претерпевает кажущееся уменьшение веса, величина которого определяется законом Архимеда: тело, погруженное в жидкость, претерпевает кажущееся уменьшение веса, равное весу вытесненной им жидкости. Правильность этого закона видна уже из того, что произвольная часть, мысленно выделенная внутри жидкости, остается в покое, хотя на ее поверхность действует давление остальной жидкости. Эта часть как будто потеряла весь свой вес, который и должен равняться равнодействующей всех гидростатических давлений на ее поверхность. Если ее заменить твердым телом одинаковой с ней формы, то равнодействующая всех давлений не изменится, т. е. останется равной весу жидкости, занимающей такой же объем, как и погруженное в жидкость тело. Если плотность d тела равна плотности d' жидкости, то тело остается в покое внутри жидкости; его кажущийся вес равен нулю. Если d больше d', то подъемная сила жидкости меньше веса тела; равнодействующая всех сил, влияющих на тело, направлена вниз, и тело тонет. Если же d меньше d', то равнодействующая направлена вверх, и тело плавает. При плавании тело настолько погружается в жидкость, что вес тела делается равным весу вытесненной им жидкости. Чем меньше плотность жидкости, тем большая часть тела погружается в нее. Так, в пресной воде корабль сидит глубже, чем в воде соленой.

Внутреннее строение жидкости сложнее строения газов. Bo-1-х, молекулы в жидкости настолько сближены, что столкновения между ними должны происходить несравненно чаще, чем в газах. Вследствие этого среднее положение, около которого движется данная молекула, меняется весьма медленно. Bo-2-х, каждая молекула находится под влиянием сил, как бы исходящих от группы соседних молекул, заполняющих так называемую сферу частичного действия, в центре которой находится рассматриваемая частица. Это — силы сцепления, или силы молекулярные. Если частица находится внутри жидкости, то все действующие на нее со всех сторон силы сцепления взаимно уравновешиваются. Для частицы, находящейся у самой поверхности жидкости, силы сцепления дают равнодействующую, направленную вовнутрь жидкости, по нормали к ее поверхности. Это относится ко всем молекулам, расстояние которых от поверхности жидкости меньше радиуса сферы частичного действия. Вследствие этого поверхностная пленка производит со всех сторон давление на жидкость; она может быть уподоблена растянутой упругой перепонке. Всякое увеличение поверхности жидкости требует затраты работы. Чем больше поверхность жидкости сравнительно с ее массой, тем большую роль должны играть силы, действующие в поверхностной пленке. Испарение объясняется тем, что отдельным молекулам, лежащим у самой поверхности и случайно обладающим в данный момент большей скоростью по направлению во внешнее пространство, удается выйти из сферы частичного действия, несмотря на удерживающую их силу сцепления. Если над жидкостью находится газ или пар другой жидкости, то вылетающие частицы отчасти отбрасываются обратно, вследствие чего испарение происходит очень медленно. В пустоте испарение доходит мгновенно до предела, когда над жидкостью пар насыщен, и настает подвижное равновесие, при котором, несмотря на непрерывный обмен частиц, количества жидкости и пара остаются без изменения. Молекула жидкости, по всей вероятности, гораздо сложнее молекулы пара, особенно когда пар находится далеко от насыщения. По всей вероятности, молекула жидкости состоит из нескольких простых молекул, соединенных в одно целое. Так, молекула воды имеет состав (Н₂О)_n, где Н₂О — состав молекулы водяного пара. При испарении сложная молекула распадается на части (физическая диссоциация). Для определения плотности жидкости существуют различные способы (см. удельный вес). Все жидкости сжимаются, т. е. их объем v уменьшается, когда увеличивается внешнее давление р. Изменение Δv объема, вызванное увеличением Δр внешнего давления, выражается формулой Δv = — βvΔр. Коэффициент β равен относительному изменению объема, вызванному изменением внешнего давления, равным единице давления, т. е., например, одной атмосферой или давлением в один кг на кв. метр поверхности жидкости; эта величина называется коэффициентом сжатия. Бэкон (1620 г.) первый описал попытку определения сжимаемости воды, наполняющей пустой свинцовый шар, который был подвергнут сжатию. Вода при этом выступила наружу, и ее сжатие не могло быть доказано. В 1701 г. Кантон впервые произвел опыт, доказавший, что вода сжимается. Принимая давление атмосферы за единицу давления, он нашел р = 0,000046, что вполне согласно с новейшими изысканиями. Дальнейшие опыты производили Перкинс (1820 г.) и Эрстед (1822 г.), который построил особый прибор для наблюдения сжатия жидкости, называемый пьезометром. Штурм и Колладон (1827 г.) приняли во внимание изменение объема сосуда и определили р для целого ряда жидкостей.

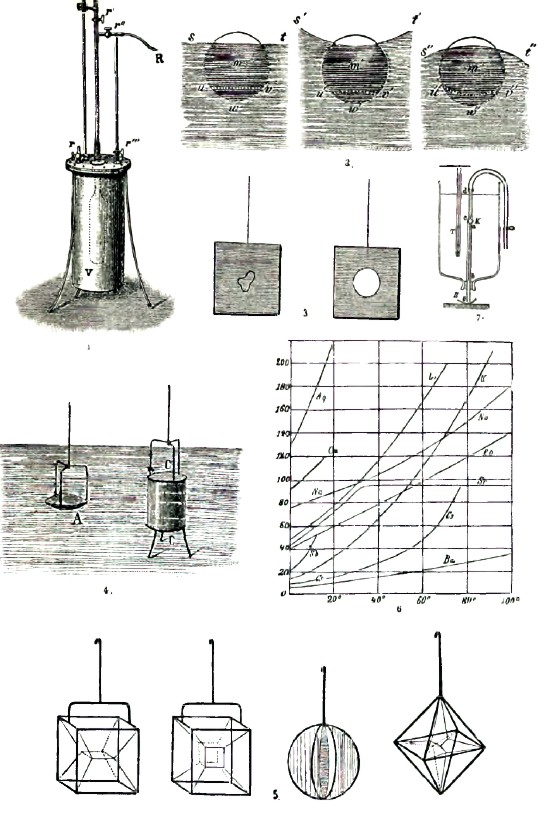
Первые весьма точные опыты производил Реньо (1847 г.) — при помощи прибора, изображенного на рис. 1. Крепкий металлический сосуд, наполненный водой, содержит продолговатый сосуд V с припаянной к нему калибрированной волосной трубкой, имеющей кран r’; в крышке вставлены кран r и трубка с краном r’’’; она может быть соединена с сосудом V помощью крана r’’. Трубка R ведет к резервуару сжатого воздуха. Сосуд V содержит испытуемую жидкость; его можно подвергнуть четырем различным комбинациям давления: 1) r’’ и r’’’ закрыты, r и r’ открыты; снаружи и внутри сосуда V давление равно атмосферному. 2) r и r’’ закрыты, r’ и r’’’ открыты; снаружи давление р сжатого воздуха на сосуд V, внутри давление атмосферное. 3) r и r’ закрыты, r’’ и r’’’ открыты; снаружи и внутри давление р. 4) r’ и r’’’ закрыты, r и r’’ открыты; снаружи давление атмосферное, внутри давление р. Высота жидкого столба в капиллярной трубке устанавливается в этих четырех опытах на различных высотах. Комбинируя результаты 4-х наблюдений, можно вычислить сжимаемость материала, из которого сделан сосуд V, а также сжимаемость жидкости, которая в нем содержится. Этим прибором пользовался также Грасси (1851 г.). Для ртути 10⁶β = 3,8, по исследованиям Амага, Де-Метца (в Киеве) и др. С повышением температуры возрастает сжимаемость жидкости. Дреккер нашел,  что сжимаемость растворов уменьшается с увеличением крепости раствора. Обширные исследования о сжимаемости жидкостей при различных температурах произвел Амага. Он нашел для 12 жидкостей (вода, эфир, алкоголь, сероуглерод и т.д.), что сжимаемость с увеличением давления уменьшается, и что при весьма сильных давлениях (несколько тысяч атмосфер) индивидуальные свойства жидкости исчезают, т.е. коэффициенты сжатия делаются близкими друг к другу. Сжимаемость эфира увеличивается с повышением температуры, но эта зависимость почти исчезает при громадных давлениях. Сжимаемость воды уменьшается при возрастании температуры до 50°, а при дальнейшем возвышении температуры сжимаемость увеличивается. Чем сильнее давление, тем слабее выражен этот минимум; при весьма сильных давлениях сжимаемость воды с повышением температуры увеличивается, как и для других жидкостей. Коэффициент теплового расширения жидкости уменьшается с увеличением давления; только для воды он увеличивается. При громадных давлениях эти коэффициенты принимают для различных жидкостей почти одинаковые значения. Температура наибольшей плотности воды понижается при увеличении давления; при очень сильных давлениях вполне исчезает сжатие воды при нагревании выше 0°. Нормальное давление поверхностной пленки зависит от формы жидкости. На рис. 2 частицы m, m’ и m” находятся на одинаковом расстоянии от плоской, вогнутой и выпуклой поверхностей жидкости. Действия частиц, находящихся внутри части сферы частичного действия, ограниченной поверхностью жидкости и симметрично расположенной поверхностью uv, u’v’ или u”v”, взаимно уничтожаются. Остается действие на центральную частицу тех частиц, которые заключаются в части uvw, u’v’w’, u”v”w”, из которых вторая меньше, а третья больше первой. Отсюда следует, что нормальное давление на выпуклой поверхности больше, а на вогнутой меньше, чем на плоской.

Лаплас дал формулу для величины нормального давления Р = К + α(1/R₁ + 1/R₂), где К нормальное давление для плоской поверхности, R₁ и R₂ радиусы кривизны двух главных нормальных сечений поверхности жидкости, считаемые положительными вовнутрь жидкости; величина α называется поверхностным натяжением; она равна силе, действующей по касательной к поверхности жидкости на единицу длины контура произвольной части этой поверхности. Гаусс дал несколько иное определение поверхностного натяжения: она равна той работе, которую необходимо затратить, чтобы увеличить поверхность жидкости на единицу, например, на 1 кв. см. Существует множество опытов, на которые можно смотреть, как на доказательства существования поверхностного натяжения в жидкости. Если, например, на поверхности ртути, налитой в глубокий сосуд, насыпать какой-нибудь порошок и затем погрузить в ртуть вертикальную толстую стеклянную палочку, то весь порошок увлекается в то углубление, которое образуется вокруг палочки, как будто ртуть покрыта кожицей, не разрывающейся при погружении палочки в ртуть. Капля, висящая на нижнем конце вертикальной тонкой трубки, содержащей жидкости, имеет совершенно ту же форму, какую принимает тонкий каучуковый лист, если на него наливать воду, заставляющую его принять форму мешочка. Стальную иглу можно осторожно положить на поверхность воды. Поверхностное натяжение воды уменьшается от прибавления спирта или эфира. Если опустить в мыльную воду проволочный четырехугольник, то легко на нем получить жидкую пленку. Если на эту пленку осторожно положить маленькое колечко из смоченной нитки (рис. 3) и затем прорвать пленку внутри колечка, то последнее принимает форму круга под влиянием действующего на него со всех сторон натяжения. Нормальное давление К для плоской поверхности определить весьма трудно. Допуская, что формула Фан-дер-Вальса (см. газы, XII, 313) приложима к жидкости, можно определить К, которое для воды оказывается около 10 000 атмосфер. Особый способ определения К дал Стефан (1886 г.). Существует множество способов опытного определения поверхностного натяжения α жидкости. Один из них  заключается в измерении высоты h, на которую жидкость поднимается в вертикальной тонкой (капиллярной) трубке, вставленной в жидкость, причем стенки трубки смачиваются жидкостью. В этом случае α определяется из формулы 2α = rδh, где r радиус поперечного, внутреннего сечения жидкости и δ плотность жидкости. Другой способ следующий: из вертикально поставленной трубки заставляют испытуемую жидкость медленно, по каплям, вытекать. Взвешивают большое число, например, 100, вытекших капель и отсюда определяют вес р одной капли. Тогда р = 2rα, где r радиус горизонтального сечения капли в наиболее узком ее месте, образующемся перед моментом отрыва капли; величина r меньше радиуса поперечного сечения трубки. Опыты показали, что с повышением температуры поверхностное натяжение всех жидкостей уменьшается, и что вообще можно положить α = α₀ (1 — βt), где α₀ значение α при 0°, и р термический коэффициент поверхностного натяжения. При критической температуре, когда плотность жидкости делается равной плотности ее насыщенного пара, получается α = 0. Когда поверхность жидкости увеличивается, то потребная для этого работа (см. выше) производится на счет тепловой энергии самой жидкости. При увеличении поверхности на единицу исчезает количество q теплоты, причем q = AT α₀β, где А термический коэффициент работы, Т абсолютная температура; α₀ и β определены выше. Когда поверхность воды увеличивается на 1 кв. см, то в ней исчезает одна миллионная малой калории. Если выражать α в мг на мм, то для ртути α = 47, для воды 7,7, для спирта 2,3, для эфира 2,0, для хлороформа 2,8, для сероуглерода 3,3 и т. д. Величина α (Мv)^2/3 называется молекулярной поверхностной энергией жидкости; здесь М молекулярный вес жидкости (например, 18 для воды), v ее удельный объем, т. е. объем ее весовой единицы. Опыты показали, что для всех жидкостей

α (Мv)^2/3 = k(τ — d),

где τ разность между критической и наблюдаемой температурами. Величина d почти всегда близка к шести; коэффициент k = 2,12, по опытам Рамзая и Шильдса. Но Дютуа и Фридерих нашли, что для различных жидкостей k колеблется между 1,53 и 2,63.

Если опустить жидкость в другую, с которой она не смешивается, и которая имеет одинаковую с ней плотность, то первая принимает вид шара (опыт Плато). Если через  этот шар провести вертикальную металлическую ось и привести ее в быстрое вращение, то и шар начинает вращаться. Он при этом сплющивается, а при большой скорости от него сперва отделяется экваториальный слой, образуя кольцо, которое затем разрывается на части. Внутри проволочного кольца можно получить жидкую чечевицу (рис. 4, А). Между двумя такими кольцами можно образовать жидкий цилиндр (с выпуклыми шаровидными основаниями). Приподнимая верхнее кольцо, можно изменить форму жидкого тела; одну из таких форм представляет катеноид, ограниченный плоскими основаниями и боковой поверхностью вращения, образующая которой есть цепная линия. При помощи проволочных фигур различного вида можно получить весьма разнообразные сочетания жидких пластинок, например, из мыльной воды. Некоторые из этих форм изображены на рис. 5.

Все подобные формы удовлетворяют следующим законам: на одном жидком ребре никогда не сходится более трех пластинок; они составляют равные между собой углы (по 120°). В одной точке внутри системы пластинок могут сходиться только четыре ребра, составляющие между собой равные углы. Вопросом о поверхностном натяжении при соприкосновении нескольких жидкостей занимался Квинке. Масло расплывается по поверхности воды весьма тонким слоем; его толщина может доходить до 0,0000016 мм. Поверхностное натяжение играет весьма важную роль в капиллярных явлениях (см. волосность). Плато и Квинке старались определить величину радиуса сферы частичного действия. Он оказывается приблизительно равным 0,05 микрона (микрон равен 0,001 мм.), что приблизительно равно 0,1 длины волны желтого света. Когда твердое тело соприкасается с жидкостью, то оно целиком или частью переходит в жидкое состояние и образует с данной жидкостью однообразную смесь, называемую раствором. Количество твердого вещества, могущего раствориться в данном количестве жидкости, имеет предел, зависящий от рода взятых двух веществ, от температуры, давления и, вообще, от физических условий, при которых совершается растворение. Когда этот предел достигнут, то раствор называется насыщенным. Растворимость определяется количеством вещества, растворяющегося в 100 частях жидкости или же находящегося в 100 частях насыщенного раствора. При соприкосновении 2-х жидкостей, не смешивающихся во всех пропорциях, также могут образоваться растворы. Растворение представляет явление крайне сложное, и в нем играет роль целый ряд различных факторов. Вопрос о растворах составляет один из главных отделов физической химии. Переход твердого вещества в жидкое при его растворении сопровождается поглощением теплоты. Поэтому растворение весьма часто сопровождается охлаждением. Но параллельно с этим играет при растворении большую роль химизм, и притом его проявления разнообразны. На раствор иногда можно смотреть, как на своего рода непрочное химическое соединение между растворителем и растворимым. Изменение плотности раствора (см. ниже) может служить доказательством того, что растворение не есть простое смешение двух веществ. Растворение солей и кислот в воде может сопровождаться распадением или образованием различных гидратов. Целая школа ученых придает огромное значение диссоциации растворенного вещества. Предполагается, что в слабых растворах почти все молекулы  растворенного вещества диссоциированы, т. е. разложены на составные части, а именно на те, которые выделяются из раствора при электролизе. Выделение растворенного вещества происходит в 3-х случаях: 1) при нагревании раствора жидкий растворитель переходит в парообразное состояние и отделяется от растворенного вещества, если последнее не летуче; в  противном случае, более или менее полное разделение раствора достигается многократной (фракционированной) перегонкой, когда растворимое и растворитель имеют различные точки кипения (спирт и вода). 2) При охлаждении слабых растворов в воде выделяется чистый лед; при охлаждении крепких растворов выделяется растворенное вещество. 3) Добавление к раствору вещества, не могущего служить растворителем, весьма часто приводит к выделению части растворенного вещества (приливание спирта к раствору поваренной соли). С повышением температуры растворимость, вообще, увеличивается, но это правило имеет исключение.

На рис. 6  изображена зависимость растворимости азотнокислых солей различных металлов от температуры. Буквы обозначают химические знаки металлов, входящих в состав соли. На горизонтальной оси отложены температуры до 100°, на вертикальной — число частей соли, растворяющихся в 100 частях воды. Из чертежа видно, какую странную особенность представляет растворимость соли стронция. Растворимость хлористого, бромистого и иодистого калия, хлористого бария и серно-калиевой соли выражается линейной функцией от температуры. Эмпирические формулы для зависимости растворимости от температуры дали Норденшельд, Этар и др. Растворимость соды растет до 38°, а затем убывает. Весьма мало меняется растворимость поваренной соли в зависимости от температуры: 35,52 частей при 0° и 40,25 частей при 100°. Цинковый  купорос имеет максимум растворимости при 81°. Растворимость железного купороса меняется весьма неправильно, в зависимости от температуры. Растворимость веществ, весьма мало растворяющихся в воде, исследовали Кольрауш и Розе. К таким веществам принадлежат соли: серно-бариевая, углебариевая, углекальциевая, иодистое серебро и др. Одна весовая часть угле-бариевой соли растворяется в N = 64 000 весовых частей воды; для углекальциевой соли (мел) N=100 000, для иодистого серебра N=1 миллиону, для бромистого серебра N = 2 миллионам. Растворимость смеси жидкости меньше суммы растворимости веществ в отдельных жидкостях. Если медленно охлаждать насыщенный раствор, то растворенное вещество иногда не выделяется, несмотря на то, что его находится в растворе больше, чем соответствует насыщению при новой более низкой температуре. Такой раствор называется пересыщенным. Раствор серно-натровой соли можно охладить до того, что он будет содержать в 8 раз больше соли, чем соответствует насыщению. Соль быстро начинает выделяться, когда в пересыщенный раствор попадает малейшая крупинка растворенной соли. Левело и Жернес выяснили сложный механизм образования пересыщенных растворов. Растворение сопровождается уменьшением объема, так называемым сжатием. Величина сжатия зависит от крепости раствора. Так, наибольшее сжатие раствора хлористого стронция в воде соответствует случаю, когда весовые количества соли и воды равны между собою. Герич (в Одессе) находит для уменьшения 8 объема воды, получаемого при образовании 100 г раствора, содержащего р% соли, следующее выражение: δ=Ср. (100 — р), где С не зависит от р, но зависит от температуры. Давление увеличивает растворимость тех веществ, растворение которых сопровождается сжатием, и уменьшает растворимость, когда при растворении происходит увеличение объема. Браун теоретически разобрал вопрос о зависимости растворимости от внешнего давления. Растворимость поваренной соли увеличивается почти на ½% при давлении в 120 атмосфер, а растворимость нашатыря уменьшается более, чем на 1% при давлении в 164 атмосферы. Всасывание растворов пористыми веществами нередко сопровождается выделением растворенного вещества. Песок и уголь удерживают часть солей из растворов; подобное относится к неклееной бумаге. Упругость р' пара раствора меньше упругости р пара растворителя. Разность р—р' относится к упругости р, как n к n + N, где n — число молекул растворенного вещества, приходящихся на N молекул растворителя. Температура t' затвердевания раствора ниже температуры t затвердевания растворителя. Понижение t—t' прямо пропорционально квадрату абсолютной температуры и числу весовых частей вещества, растворенных в 100 частях растворителя, и обратно пропорционально молекулярному весу и скрытой теплоте плавления растворенного вещества. Теплоемкость растворов солей в воде меньше суммы теплоемкостей воды и соли. Температура наибольшей плотности водных растворов лежит ниже 4°С, температуры наибольшей плотности чистой воды. Относительно взаимного растворения жидкости следует отличать три случая: 1) некоторые жидкости вовсе не растворяются одна в другой или, по крайней мере, незаметно мало (масло и вода); 2) некоторые жидкости могут быть смешаны во всех пропорциях (алкоголь и вода, многие кислоты и вода, хлороформ и сероуглерод и т. д.); 3) существуют жидкости, растворяющие друг друга в определенных количествах. Если смесь таких двух жидкости сболтать и затем дать ей устояться, то она разделяется на две части: внизу более тяжелая, наверху более легкая из жидкости, причем каждая представляет насыщенный раствор другой жидкости (вода и эфир, алкоголь и сероуглерод). Взаимное растворение жидкости сопровождается изменением температуры. При смешении хлороформа и бензина температура повышается на 7,2°. Смешение уксусного эфира с алкоголем сопровождается понижением температуры на 2,4°. Смешение жидкости сопровождается иногда весьма значительным уплотнением. Весьма интересный пример такого уплотнения представляет смешение воды и алкоголя, подробно исследованное Д. И. Менделеевым. Сжатие доходит до 4,15%, суммы объемов воды и алкоголя для случая смешения 45,88 частей алкоголя и 54,12 частей воды. Растворенное вещество по своим свойствам напоминает многие свойства газов. Так, например, оно, подобно газам, стремится расшириться, т. е. занять по возможности больший объем — оно диффундирует в чистый растворитель, если таковой соприкасается с раствором. Далее, растворенное вещество производит особого рода давление, называемое осмотическим; оно вполне аналогично давлению газов. Траубе (1867 г.), Пфеффер (1877 г.) и др. показали целый ряд способов получения так называемых полупроницаемых перепонок, при помощи которых могут быть изучены явления осмотического давления. Удобнее всего взять сосуд из пористой глины и пропитать его сперва раствором медного купороса, а затем раствором железисто-синеродистого калия. Тогда все поры сосуда затягиваются полупроницаемой пленкою, свободно пропускающей через себя воду, но задерживающей в большей или меньшей степени растворенное вещество. Оствальд, Вант-Гофф, Пернет и Тамман (в Юрьеве) развили учение об осмотическом давлении в растворах. Оно играет важную роль и в органическом мире. Так, например, исследования Владимирова (1891 г.) показали, что осмотическое давление в клетках бактерий весьма велико. В клетках моркови оно может доходить до 18 атмосфер. Растворы, обладающие одинаковым осмотическим давлением, называются изотоническими; они обладают одинаковой упругостью пара и одинаковой температурой замерзания. Названные выше ученые, а также Рауль, Аррениус и др., развили далее учение о близком сходстве ряда основных свойств растворов и газов. Осмотическое давление при неизменной температуре пропорционально концентрации раствора или обратно пропорционально объему, занимаемому данным количеством растворенного вещества (закон Мариотта); осмотическое давление пропорционально абсолютной температуре (закон Гей-Люссака). Одинаковые объемы изотонических растворов содержат при данной температуре одинаковое число молекул, равное числу газовых молекул, находящихся в том же объеме, при тех же давлении и температуре (закон Авогадро). Эти законы перестают быть верными для растворов электролитов (соли и кислоты). Планк и Аррениус объясняют эти отступления тем, что электролиты в растворах отчасти диссоциированы.   Когда различные части одной и той же жидкости обладают неодинаковыми движениями, то между слоями жидкости развивается внутреннее трение. Коэффициент k внутреннего трения, который еще называется вязкостью данной жидкости, определяется формулой f = ksdv : dx, где s — поверхность соприкосновения двух слоев жидкости, dv — разность скоростей двух слоев, расстояние которых равно dx, причем dx перпендикулярно к s; наконец, f — сила, замедляющая движение одного и ускоряющая движение другого слоя. Обыкновенно принимают вязкость воды при 0° равной 100. В этом случае k называется удельной вязкостью. Когда жидкость касается неподвижного твердого тела, и скорость слоя жидкости, непосредственно прилегающего к поверхности твердого тела, не равна нулю, то между жидкостью и твердым телом появляется трение. Сила f, действующая в этом случае на рассматриваемый слой жидкости, выражается формулой f = csv, где s — поверхность соприкасания слоя и v — его скорость. Величина с называется коэффициентом внешнего трения жидкости. Отношение k : с называется коэффициентом скольжения. Коэффициент k внутреннего трения определяется удобнее всего по так называемому способу капиллярных трубок. Заставляют жидкость под определенным давлением Р протекать через капиллярную трубку, радиус сечения которой R и длина которой L. Если Q объем жидкости, протекшей через трубку во время Т, то коэффициент k внутреннего трения жидкости определяется формулой k = πPTR⁴ : 8QL. Для воды коэффициент трения не зависит от материала трубки. На рис. 7 изображен простой прибор, могущий служить для определения величины k. Капиллярная трубка ab оканчивается внизу более широкой частью be, а наверху расширением k, от которого идет далее широкая трубка cd, суженная в с. К концу d прикреплена каучуковая трубка, снабженная зажимом. Вся трубка ed находится внутри сосуда с водой, температура которой определяется термометром Т. Открыв зажим, всасывают испытуемую жидкости в трубку ed до точки, лежащей несколько выше с, и затем определяют время Т, в течение которого вся жидкость вытекает через капиллярную трубку. Кулон, Гельмгольц, Маргулес и др. дали другие способы определения величины k. Способ Кулона основан на наблюдении поворотных колебаний круглой металлической горизонтальной пластинки, вращающейся внутри жидкости. Если за единицу длины, времени и массы принять сантиметр, секунду и грамм, то для ртути k = 0,0158, для воды k = 0,0119. С повышением температуры коэффициент k весьма быстро уменьшается. Так, для воды k при 70° в 4 раза меньше, чем при 0°. Вязкость жидкой углекислоты при 15° в 14,6 раз меньше вязкости воды; вязкость глицерина при 2,8° в 2 500 раз больше вязкости воды. С увеличением давления вязкость воды уменьшается, а вязкость насыщенных растворов поваренной соли и нашатыря в воде увеличивается. Вязкость растворов иногда больше, иногда меньше вязкости воды. Движение жидкости рассматривается в особом отделе механики, называемом гидродинамикой. Вместе с гидростатикой (см. выше) она составляет так называемую гидромеханику. Когда жидкость, подверженная силе тяжести, вращается около вертикальной оси, то ее поверхность перестает быть плоской и делается поверхностью параболоида вращения; всякая плоскость, проходящая через ось вращения, пересекает ее по параболе, и особый интерес представляет вытекание жидкости из малых отверстий и когда образуются так называемые жидкие струи. Если v — скорость жидкости и s — площадь отверстия, то количество Q жидкости, вытекающей в единицу времени, определяется формулой: Q = avs, где а правильная дробь, которая для воды приблизительно равна 0,62. Это число равно отношению площади поперечного сечения струи к площади отверстия. Сжатие струи было замечено еще Ньютоном. По теории Байэра, оно равно π²: 8 = 0,617, что хорошо согласуется с наблюдениями. Вблизи отверстия жидкая струя воды прозрачна и гладка; на некотором расстоянии от отверстия она делается непрозрачной, и сечение ее периодически увеличивается и уменьшается. Оказывается, что она перестает быть сплошной, распадаясь на отдельные большие капли, совершающие как бы пульсации, располагаясь попеременно то по направлению струи, то по направлению к нему перпендикулярному. Между каждыми двумя большими каплями помещается одна малая. Наблюдать эти капли можно, например, при моментальном освещении струи электрической искрой или путем моментального фотографирования. Течение жидкости через капиллярные трубки определяется законами Пуазеля, приводящими к формуле, которая уже была указана выше при определении коэффициента внутреннего трения. Колебательные движения поверхностных частиц жидкости вызывают всем известное явление жидких волн, которые весьма тщательно были изучены братьями Э. и В. Вебер (1825 г.). В движениях принимают участие частицы, лежащие на глубине, не превышающей более чем в 350 раз высоту волн. Скорость распространения волн зависит от глубины жидкого слоя, от длины волны, которую следует считать поперек волн, от плотности жидкости и от поверхностного натяжения. Движение воздуха (ветер) у поверхности жидкости может значительно влиять на форму и скорость волн. Гельмгольцу принадлежит учение о вихревых движениях (см.) в идеальной жидкости, вязкость которой равна нулю; он доказал, что вращательные, или вихревые, движения не могут ни образоваться, ни уничтожаться в идеальной жидкости. Раз они существуют, они должны оставаться вечно. На этом основана знаменитая теория вихревых атомов, предложенная лордом Кельвином (В. Томсон). Частицы, участвующие во вращательном движении, всегда в нем участвуют, т. е. перемещаются из одного места в другое вместе с вихрем. Вихревая нить не может иметь свободного конца внутри жидкости; она должна или оканчиваться у поверхности жидкости или быть замкнутой; вихревая нить не может быть перерезана. Две нити не могут пересечься, а потому петля в нити, раз она существует, не может раскрыться. Произведение угловой скорости вращения на площадь поперечного сечения нити есть величина постоянная вдоль всей нити. Вихревые нити действуют на частицы внешней для них жидкости, заставляя их двигаться со скоростью, законы которой вполне аналогичны законам действия электрических токов на магнитный полюс. Вихревое кольцо имеет в неограниченной жидкости равномерное поступательное движение по направлению движения жидкости внутри кольца. В неидеальной жидкости, обладающей вязкостью, возможно образование и исчезновение вихревых движений.

О. Хвольсон.