Электрохимия

Электрохимия, отдел физической   химии, посвященный изучению процессов перехода химической энергии в электрическую и обратно, другими словами — исследованию химических реакций, которые вызывают или вызываются током электронов или их переносом, как, например, в гальванических батареях и при электролизе. Начало истории электрохимии можно отнести к 1799 г., когда Вольта (см. ХII, 422/26) изобрел гальваническую батарею, известную под именем Вольтова столба.

Дальнейшие исследования Никольсона и Карлейля, Дэви, Берцелиуса и Гизингера (см. химия неорганическая, XLV, ч. 2, 320) определили то направление, которое приняла химия в начале XIX в. Это направление характеризуется господством электрохимической теории, предложенной Дэви и видоизмененной Як. Берцелиусом.

Согласно учению Дэви (см.) все вещества при соприкосновении друг с другом получают противоположные электрические заряды. А так как мельчайшие или элементарные частички могут двигаться вполне свободно, то они могут, согласно основному закону, взаимно притягиваться вследствие их электрических сил. «При теперешнем состоянии наших знаний было бы напрасным желание искать более отдаленные причины электрических сил или причину, почему два различных тела при соприкосновении противоположно электризуются. Связь же их электричеств с их химическим сродством выступает довольно ясно. Почему же не может быть, что электричество и сродство представляют одно и то же, и являются существенным свойством материи?» Далее Дэви указывает, что, измерив электрические силы, требующиеся для разложения различных соединений, мы могли бы расположить все тела в порядке электрических сил, присущих телам, причем порядок этот вполне соответствовал бы степени химического сродства тел друг к другу; явления выделения теплоты и света при многих химических реакциях служат доказательством его электрической теории. Теория Дэви удовлетворяла всем требованиям, которые следует предъявлять научной теории: она исходила из простой и ясной идеи, наблюдаемые явления объяснялись ею легко понятным способом, она позволяла делать выводы, которые были доступны опытной проверке.

Благодаря этой гипотезе Дэви быстро прославился, а когда ему удалось разложить едкие щелочи, то многие думали, что для химии начинается новая эра. Но господство теории Дэви было непродолжительно; уже через десять лет она сменилась новой теорией Берцелиуса, наложившей отпечаток на большинство работ первого сорокалетия XIX в. В основе его теории лежит дуалистическое воззрение, согласно которому в составе каждого тела можно различать две части: сложные тела происходят от соположения атомов. Когда атом одного элемента соединяется с атомом другого, то происходит соединение первого порядка, например из K и О получается окись калия (KО по Берцелиусу), из S и О — серная кислота (SO₂ по Берцелиусу). (Окись калия и серная кислота, соединяясь между собой, дают начало соли —   сернокислому калию (KО·SO₃) — соединению второго порядка. Двойные   соли, например квасцы, представляют соединения третьего порядка и т. д. Во всех происшедших телах мы можем различать соположенные две составных части, обладающие противоположными свойствами. По Берцелиусу, различное электрическое состояние атомов является основным свойством каждого элемента: в каждом атоме находятся два электрически противоположных полюса, только количество электричества в обоих полюсах неодинаково, и каждый атом является таким образом как бы униполярным; в атомах металлов количество электричества, сосредоточенного в положительном полюсе, превышает таковое в отрицательном полюсе, и таким образом атомы металлов являются электроположительными, в атомах же металлоидов (например, серы, фосфора) находится избыток отрицательного электричества, и они являются электроотрицательными.

Все элементы Берцелиус расположил в ряд по количеству свободного электричества, заключающегося в их атомах: в начале ряда поставлены наиболее электроположительные металлы — K, Na, Li, Sr, Ва, Mg; затем следуют другие металлы; срединное положение занимает водород, отделяющий металлы от неметаллов; за ним — Si, Те, Sb, С, В, . . J . . ., Вт, Cl, F, N, S, О. Кислород является абсолютно электроотрицательным элементом, так как он соединяется со всеми элементами. Каждый элемент в ряду является электроположительным по отношению ко всякому последующему ряду и электроотрицательным по отношению ко всякому предыдущему.

Электрохимическая теория Берцелиуса представляла стройную систему, позволявшую охватывать одним взглядом почти весь громадный материал неорганической химии; номенклатура и дуалистическое представление Берцелиуса сохранились и до настоящего времени: химики продолжают говорить о положительной и отрицательной составных частях соединения. Дальнейшие успехи химии и физики опровергли основные положения теории Берцелиуса, но затем, к концу XIX и в начале XX столетия она возродилась в видоизмененной форме (см. далее).

Законы Фарадея. Еще в 1833 г. Фарадеем (см.) были установлены следующие соотношения между количеством электричества, прошедшего через раствор соли, и весом выделившегося на катоде металла.

Первый закон электролиза: количество разлагаемого вещества пропорционально полному количеству проходящего электричества.

Второй закон: при одном и том же количестве электричества, прошедшем через различные электролиты, весовые количества разложенных электролитов или выделившихся ионов пропорциональны химическим эквивалентам этих веществ.

Эквивалентами называются такие количества элементов, которые способны замещать одну весовую часть водорода или соединяться с одной весовой частью водорода. Поэтому для металлов первой группы периодической системы эквивалент равен атомному весу, второй группы — одной половине атомного веса, эквивалент алюминия равен 1/3 атомного веса, в солях закиси железа его эквивалент равен 56/2 = 28 в солях окиси 18 2/3 и т. д.

По закону Фарадея следует, что при прохождении одного и того же количества электричества через ряд вольтаметров, в коих находятся различные соли и кислоты (например, НСl, AgNO₃, CuCl₂, FeCl₂, FeCl₃), количества элементов, выделившихся на катоде (т. е. Н, Ag, Сu, Fе и др.), будут относиться как 1:107,66:31,78:27,92 и т. д.

Электрохимическим эквивалентом (ε) называется такое количество вещества, которое выделяется током силой в 1 ампер в течение одной секунды.

Количество электричества, которое нужно пропустить через раствор электролита, чтобы выделился один грамм-эквивалент катиона или аниона, равно 96,494 кулонов; оно обозначается через F.

В следующей таблице ε — число мг, выделяющихся при прохождении 1 ампера в 1 секунду, а, h — число г, выделенных 1 ампером в 1 час.

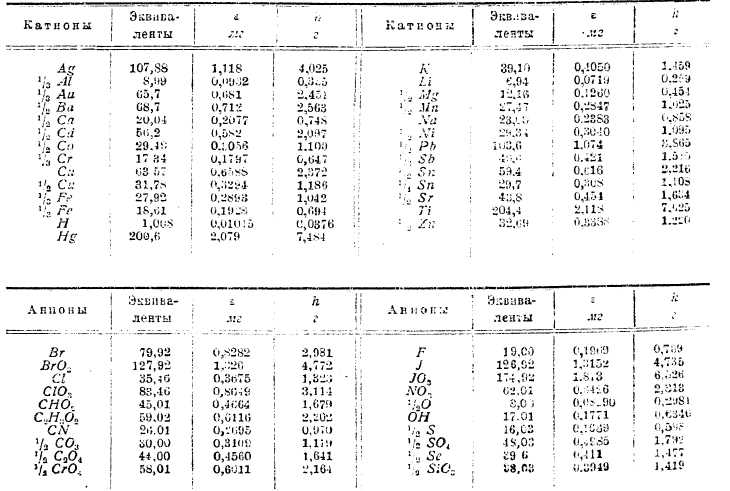
Согласно законам Фарадея, электричество через растворы двигается вместе с веществом: при прохождении тока катион направляется к катоду (отрицательному полюсу), а анион — к аноду, причем все одновалентные катионы (например, Н^·, K^·, Ag^· и т. п.) несут один заряд положительного электричества (IF), двухвалентные (Mg^·, Ca^·, Fe^·, Сu^· и т. п.) — два заряда (2F), трехвалентные — три заряда (3F), равным же образом  двухвалентные анионы (например, SO₄”) несут вдвое больший заряд отрицательного электричества сравнительно с одновалентвыми (Сl^·, Br^·, NO₃^· и т. п.). Таким образом, наряду с законом кратных отношений мы имеем закон кратных зарядов электричества и подобно тому, как первый закон нашел объяснение в атомистической теории, так и второй приводит к понятию об атомах электричества. «Если применить», говорит Гельмгольтц, «атомистическую теорию к электрическим процессам, то в соединении с законом Фарадея она приводит к поразительным следствиям. Если мы допускаем существование химических атомов, то мы принуждены заключить отсюда далее, что также и электричество, как положительное, так и отрицательное, разделяются на определенные количества, которые играют роль атомов электричества». Идея Гельмгольтца о существовании атомов электричества, высказанная в 1881 г., к настоящему времени (1936) получила широкое развитие: ока подтвердилась рядом исследований над катодными лучами и радиоактивными телами. Был открыт электрон — атом отрицательного электричества, масса коего составляет 1/1840 массы атома водорода (см. электронная, теория). Понятие об атомах электричества позволяет более наглядно представить перенос электричества в растворах: каждый одноатомный (одновалентный) ион несет один атом электричества, двухвалентный — два атома, трехатомный — три и т. д.

По теории строения атомов электрический нейтральный атом каждого элемента содержит такое число электронов, какое требуется, чтобы оно вполне могло нейтрализовать весь положительный заряд атома. Если из нейтрального атома выделится один электрон, получится ион, несущий один положительный заряд (катион); если выделятся два электрона, получится катион с двумя зарядами (двухатомный) и т. д.

Если к нейтральному атому элемента, например Cl, Вr и т. д. присоединить один электрон, получится одноатомный анион, присоединятся два электрона — получится двухатомный анион и т. д. Реакцию разложения соли на ионы можно изобразить следующим уравнением:

CuCl = Сu⁺⁺ + 2Сl’ причем протекает 2F: SnCl₄ = Sn⁺⁺⁺⁺ + 4Сl’, причем протекает 4F.

Ионы отличаются от атомов какого-либо элемента тем, что несут определенный заряд, иными словами — некоторый избыток электричества положительного (катион) пли отрицательного (анион) сравнительно с таковым нейтрального атома. Ввиду ничтожно малой массы электрона выделение или присоединение одного или нескольких электронов не может отразиться заметным образом на массе иона, но сообщает последнему свойства, резко различающиеся от свойств нейтрального атома элемента.

Заряд электрона, согласно последним измерениям, равен 4,774·10^-10 электростатических единиц системы (в CGS) =   1,59·10^-20 электромагнитных единиц = 1,59·10^-19 кулонов. Столько же положительного электричества несет каждый одноатомный катион, двухатомный — вдвое больше и т. д. Электрическое действие этих зарядов, несмотря на их кажущуюся незначительность, громадно: из определений, произведенных В. Вебером. Максвеллом и другими, оказалось, что оба электричества, которыми заряжены ионы одного миллиграмма воды, будучи разделены и помещены на два шара, удаленные друг от друга на расстоянии одного километра, должны были бы вызвать между этими шарами силу притяжения, равную, приблизительно, весу 100 000 килограммов (!!).

Открытие законов электролиза подорвало доверие к электрохимической теории, ибо оказалось, что эквивалентные количества всех элементов несут одинаковое количество электричества, а не различное, как требовалось по теории. Но в то время еще не было выработано точного различия понятий: электрическое напряжение и количество электричества. Одно и то же количество электричества нужно для выделения эквивалента любого элемента, но не одна и та же электровозбудительная сила, а так как энергия измеряется произведением количества электричества на эл. с., то и не одно и то же количество энергии.

Далее, с расцветом органической химии, с открытием явлений замещения атома водорода таким электроотрицательным элементом, каким является хлор, теория Берцелиуса с середины XIX в. была, можно сказать, забыта, но открытия последней четверти этого столетия привели к тому, что идея Берцелиуса: «электричество есть первая причина деятельности окружающей нас природы» лежит в основе, наших представлений, как о строении материи, так и о химическом сродстве. В 1881 г. Гельмгольц в своей «Фарадеевской лекции», наряду с идеей об атомах электричества, высказал следующее: «Я полагаю, что факты не оставляют никакого сомнения в том, что самые могучие из химических сил имеют электрическое происхождение». Дальнейшие успехи физики и химии подтвердили это мнение.

Электропроводность растворов. Электропроводностью называется способность тела проводить электричество. За единицу электропроводности, по Ф. Кольраушу, принимают электропроводность такого тела, столб которого в 1 см длиной и в 1 кв. см сечения обладает сопротивлением в 1 Ом.

Хорошо проводящие водные растворы   кислот при 40°С  обладают почти такой электропроводностью. Выраженную в  таких единицах электропроводность   Ф. Кольрауш предложил обозначить через κ. Если тело в 1 см длиной и   1 кв. см сечения обладает сопротивлением в ω Ом, то его удельная электропроводность κ:

Κ = 1/ω

При изучении электропроводности  растворов сравнивают часто не удельную, а эквивалентную электропроводность

Λ = κ/η, где обозначает число грамм-эквивалентов растворенного тела в 1 куб. см раствора. Отсюда  φ=1/η показывает число куб. см раствора, содержащих один грамм-эквивалент растворенного тела.

Таким образом, эквивалентная электропроводность (Λ=κ/η=κφ)  представляет электропроводность слоя раствора, толщиной в 1 см и в φ кв. см сечения. Такой слой раствора содержит 1 грамм-эквивалент растворенного тела.

В. Оствальд определял молекулярную электропроводность как электропроводность слоя раствора, расположенного между параллельными электродами, отстоящими друг от друга на расстоянии 1 см и имеющими такое протяжение, что между ними находится раствор 1 грамм-молекулы (1 моля) растворенного тела; так, например, если раствор нормальный (содержит моль), то поверхность каждого электрода 1 000 кв. см, ибо тогда объем слоя   равен 1 литру; если раствор санти-нормальный (0,01 м²), то поверхность   каждого электрода равна 100 1000 кв. см;   одним словом, если v обозначает  число литров раствора, заключающих одну грамм-молекулу, то поверхность   каждого электрода 1 000 v см². Если κ — удельная электропроводность, то молекулярная электропроводность μ = 1 000 vκ. Нетрудно видеть, что κ (или μ) показывает количество электричества (в кулонах), проходящее через каждое сечение раствора в 1 секунду при падении потенциала в 1 вольт на протяжении 1 см.

По своей электропроводности тела очень различаются: металлы сравнительно хорошо проводят электричество; такие тела, как стекло, парафин, каучук, сера и т. п. — плохо. Жидкости же, за исключением ртути и расплавленных металлов, все оказывают значительное сопротивление прохождению электрического тока. Химически чистая вода, перегнанная в разреженном пространстве и охлажденная в платиновом холодильнике, оказывается очень плохим проводником: сопротивление, какое оказывает прохождению электричества столб такой воды длиной в 1 м и 1 кв. мм сечения, равно сопротивлению медной проволоки такого же сечения, имеющей такую длину, что луч света (проходящий, как известно, 300 000 км в 1 секунду) пробежит такой путь в 2 мин. 12 сек. Но стоит только такой воде постоять несколько минут на воздухе, и ее электропроводность увеличится в несколько раз. Другие жидкости, например спирт, глицерин, равно как безводная серная кислота, жидкий (безводный) хлористый водород и т. п., обладают очень незначительной электропроводностью. При растворении же кислот (оснований и солей) в воде получается раствор, электропроводность которого в несколько тысяч и даже миллионов превышает электропроводность воды и данной кислоты. Но как ни велика электропроводность водных растворов, она по сравнению с электропроводностью металлов является незначительной. Одним из лучших проводников является раствор (30,4%) серной кислоты, электропроводность которого выражается при 18°С. в ртутных единицах числом 0,00007, т. е. сопротивление столба серной кислоты будет в 10⁵/7 = 14 290 раз больше, чем сопротивление одинакового с ним столба ртути.

Удельная электропроводность меняется с концентрацией раствора, и при известной концентрации наблюдается максимум электропроводности. Существование такого максимума обусловливается тем, что смешиваемые тела в отдельности почти не обладают электропроводностью, которая приобретается актом растворения. Сперва электропроводность довольно быстро возрастает, почти пропорционально концентрации (особенно у КОН, NaOH, НСl, HNO₃ и т. п. соединений), затем кривая достигает максимума (у KОН при m между 6 и 7, у NaOH при m между 4 и 5, у НСl и HNO₃ при m между 5 и 6) , и затем начинает медленно понижаться. Иная картина получается для молекулярной и эквивалентной электропроводности: молекулярная электропроводность при уменьшении концентрации раствора быстро увеличивается и стремится к известной предельной величине для каждого электролита. Следующая таблица эквивалентной электропроводности  Λ дает более полное представление о ходе увеличения молекулярной электропроводности растворов по мере их разжижения (v обозначает число литров, содержащих один грамм-эквивалент растворенного тела).

Эквивалентная электропроводность при 18°:

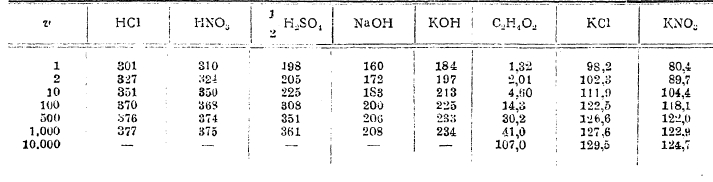
Как видно из таблицы, наибольшей электропроводностью отличаются кислоты, причем соляная кислота и азотная обладают почти одинаковой электропроводностью; серная кислота уступает им в этом отношении. За кислотами следуют щелочи, причем электропроводность растворов едкого кали более таковой для едкого натра. Из солей наибольшей электропроводностью обладают галоидные соли калия и натрия. Не приводя чисел для электропроводности других тел, мы укажем только следующие выводы.

Молекулярная электропроводность одноосновных кислот HCl, HJ, HBr, HNO₃ -  почти одинакова. То же самое замечается для галоидных солей калия и аммония, для хлористого бария, стронция и кальция. Почти одинаковой молекулярной электропроводностью обладают сернокислые соли Сu, Zn и Mg.

В солях щелочных металлов наибольшей электропроводностью обладают соли K и аммония, затем следуют соли натрия.

На основании чисел таблицы можно сделать следующий вывод: для каждой  соли электропроводность стремится   к известному пределу, который будет  представлять молекулярную электропроводность при очень большом разведении.

Что касается кислот, то они распадаются на две группы: к первой принадлежат так называемые сильные кислоты, каковы HNО₃, НСl и т. п.; для   них молекулярная электропроводность     и в крепких растворах достигает довольно значительной величины (например, для НСl А₁ = 301); при разведении же  раствора электропроводность хотя и  возрастает, но сравнительно немного (c 301 до 377 для НСl при увеличении разжижения от v = 1 до v = 1 000), и приближается ассимптотически к некоторому пределу, от которого недалеко уже при v = 1 000. Вторую группу составляют слабые кислоты, например уксусная C₂H₄O₂, электропроводность которых в крепких растворах очень мала (для C₂H₄O₂ А₁ =  1,32), с разжижением же раствора она сильно увеличивается (например, с 1,32  до 107,0 для C₂H₄O₂ при увеличении объема от v=1 до с = 10 000) и даже при самых больших разведениях (например, при v = 10 000), доступных опытному исследованию, далека от предела.

Закон Кольрауша. Опыты Кольрауша показали, что электропроводность электролита может быть вычислена как сумма двух слагаемых из коих одно характерно для катиона, другое – для аниона. Каждому электрохимическому элементу (например, K, H, Ag, NH₄, Cl, J, NO₃, C₂H₃O₂)  в разведенных водных растворах принадлежит определенное (постоянное) сопротивление все равно из какого бы электролита он ни выделился. Зная это сопротивление, которое может быть определено для каждого элемента, можно вычислить электропроводность каждого разведенного раствора. Одним словом: электропроводность растворов – свойство аддитивное.

Основываясь на этом, можно для эквивалентной электропроводности вывести следующее выражение:

где F – заряд грамм-эквивалента, U – скорость передвижения катиона, а V – аниона; l_a = FV, а l_k – подвижность катиона, l_a – подвижность аниона, а η – число грамм-эквивалентов в 1 куб. см). «Подвижность ионов» (l_k и l_a) в водном растворе при 18°С дана в следующей таблице:

Пользуясь числами этой таблицы, можно вычислять электропроводность растворов различных электролитов. Например, электропроводность 0,001 нормального раствора KCl будет равна А₁₀₀₀ = 63,7+64,4 = 128,1 (найденная опытом — 127,6).

Как видно, величины подвижности находятся в зависимости от концентрации: чем более разведен раствор, тем более величина подвижности. Объяснение этому дает теория электролитической диссоциации (см. далее).

Кольрауш показал, как, пользуясь его законом, можно на основании его измерения электропроводности растворов малорастворимых тел определить их концентрацию. Были выведены и другие закономерности. Не останавливаясь на них, переходим к изложению теорий, объясняющих процесс прохождения тока. |

Для того, чтобы объяснить явление прохождения тока через растворы электролитов, Клаузиус (1857) высказал  гипотезу, что ионы, на которые распадается соль (например, Nа и Сl’ из NaCl), двигаются в растворе свободно и независимо друг от друга. По старой  теории электролиза, единственным агентом, разлагающим молекулы электролита на ионы, была электровозбудительная сила. Клаузиус показал,  что по этой теории, пока электровозбудительная сила ниже известного предела, не должно существовать ни разложения, ни тока; но как только электровозбудительная сила достигнет этого предела, должно  начаться электролитическое разложение, сопровождаемое сильным током.   На самом деле ток проходит через раствор при всякой электровозбудительной силе, и сила тока возрастает прямо пропорционально электровозбудительной силе, какова бы ни была ее  величина. По Клаузиусу, в жидких телах, равно как и в газообразных, происходит как бы постоянная пляска молекул, причем некоторые молекулы тела, находящегося в растворе, приобретают настолько большую скорость, что при встрече с другой молекулой одна или обе молекулы разрываются, и отдельные части их отправляются искать себе, по выражению Максвелла, новых партнеров; при прохождении же тока электровозбудительная сила именно и проявляет свое действие в виде направляющей силы на эти временно разделенные молекулы, заставляя одни из составных частей (ионов) двигаться по одному направлению, а другие по противоположному. Таким образом, Клаузиус принимал существование (хотя в очень незначительном количестве) свободных ионов в растворах. Хотя исследования других физиков и химиков, в особенности работы Гитторфа (1853—1859) и Кольрауша (1877), исследовавшего электропроводность растворов большого количества солей, по-видимому подтвердили гипотезу Клаузиуса, последняя не обратила внимания на себя химиков.

Теория электролитической диссоциации. В 1884—1887 гг. появились работы молодого шведского ученого Сванте Аррениуса, в коих он для объяснения явления электропроводности растворов предположил, что в растворе электролит находится в двух состояниях: в активном, в котором он способен проводить электричество, и неактивном, в котором он этой способностью не обладает.

В дальнейших работах он указывает, что активность молекулы зависит от ее диссоциации на ионы. В растворах таких тел, как сильные кислоты, соли и основания, большая часть молекул находится в диссоциированном состоянии, например в нормальном растворе хлористого калия около 75% молекул являются разложенными, а в децинормальном — 85%, в сантинормальном — около 93% и т. д. Чем более разведенным является раствор, тем более число диссоциированных молекул, а, следовательно, при прибавлении воды число ионов увеличивается, и молекулярная электропроводность растворов должна увеличиваться, как это и наблюдается для водных растворов. Эго увеличение идет сначала быстро, затем медленнее, приближаясь ассимптотически к некоторому пределу. Этот предел достигается лишь тогда, когда все молекулы распадутся на ионы, что возможно лишь при бесконечно большом разведении (или большом количестве воды, в коем растворена грамм-молекула электролита). Так как электричество движется только с ионами, то ясно, что растворы, в коих  число диссоциированных молекул велико, хорошо проводят ток; растворы  же таких тел, которые от действия  воды мало диссоциируют (например, органические кислоты, муравьиная, уксусная и др.), хотя и проводят ток, но несравненно менее, чем растворы минеральных кислот.

Если одни свободные ионы участвуют в проведении тока, то, основываясь на измерении молекулярной теории электропроводности, можно определить степень или коэффициент диссоциации (α) ту долю молекул электролита, которая  подверглась диссоциации. Тот факт, что при возрастающем разбавлении величина  μ, т. е. молекулярная электропроводность, увеличивается, объясняется тем, что при прибавлении растворителя число диссоциированных молекул увеличивается, а вместе с этим возрастает число переносящих электричество ионов. Нетрудно видеть, что, так как молекулярная электропроводность пропорциональна числу распавшихся на ионы молекул, то дробь α=μ_v/μ_∞ (где μ_v  — молекулярная электропроводность при разведении v, а μ_∞  при бесконечном разведении) выражает степень диссоциации, т.е. какая часть молекул электролита распалась на ионы. Недиссоциированная часть молекул равна 1 - μ_v/μ_∞

Зная степень диссоциации  α, можно вычислить значение коэффициента i, показывающего, во сколько раз осмотическое давление данного раствора электролита превышает «нормальное» давление (см. растворы, XXXV, 681 сл.). Так как осмотическое давление при прочих равных условиях пропорционально количеству молекул, находящихся в данном объеме раствора, то _і показывает, во сколько раз число молекул и ионов (играющих по отношению к осмотическому давлению такую, же роль, что и молекулы) больше того какое находилось бы, если бы все молекулы были бы в нормальном состоянии, т. е. в недиссоциированном состоянии. Отсюда ясно, что і равно отношению суммы недиссоциированных молекул и ионов к числу всех молекул, которые находились бы в растворе, если бы ни одна молекула не была диссоциирована.

Для бинарных электролитов (например, NaCl, НСl, HNO₃ и т. п.) i вычисляется по следующему уравнению:

где α — степень диссоциации, а n — число молей в растворе.

Таким образом, на основании измерения электропроводности можно вычислить величину і, которая определяется на основании криоскопических и эбулиоскопических наблюдений. Вычисленные Аррениусом значения показались вполне совпадающими с опытными данными. Это близкое совпадение чисел указало на плодотворность гипотезы Аррениуса, позволившей установить количественную зависимость между столь разнообразными величинами, как понижение температуры замерзания (а, следовательно, осмотическим давлением и др.) и электропроводностью растворов.

Гипотеза С. Аррениуса, столь резко расходившаяся с установившимися взглядами на прочность таких соединений, как НСl, NaCl и т. п., не могла не вызвать возражения со стороны наиболее авторитетных химиков. Но благодаря исследованиям В. Оствальда, его учеников — П. Вальдена, Нернста и мн. др. (см. XLV, ч. 2, 327) — было добыто множество фактов, ее подтверждающих, и она превратилась в теорию, разъяснившую многие вопросы, касающиеся процессов не только в химии и технике, но и в биологии, указавшую точные математические зависимости между самыми разнообразными величинами, позволившую предугадать многие свойства растворов. Одним словом, теория электролитической диссоциации оказалась надежной путеводительницей в том лабиринте сложных явлений, которые представляют растворы. Благодаря этой теории получили простое и ясное объяснение многие свойства растворов, как-то: аддитивность, плотность, электропроводность разведенных растворов, термонейтральность растворов солей, близкая теплота нейтрализации кислот (см. термохимия, XLI, ч. 7, 572 сл.) и т. д. Основываясь на теории электролитической диссоциации, Нернст показал, как, с одной стороны, зная осмотическое давление и, с другой стороны, подвижность ионов, входящих в состав данного электролита, можно вычислить коэффициент диффузии. Исходя из этого, он создал теорию концентрационных токов, объяснил происхождение электровозбудительной силы, возникающей при соприкосновении металлов и жидкостей. Он ввел понятие об электролитической упругости растворения: подобно тому, как многие твердые тела обладают способностью растворяться, или упругостью растворения, так и металлы, приходя в соприкосновение с растворами их солей, обладают способностью посылать в последние ионы, т. е. атомы, но только без валентных электронов. Эта способность называется электролитической упругостью.

Принимая во внимание электролитическую упругость растворения, можно легко объяснить процессы в элементах Даниэля и ему подобных (см. гальванизм, XII, 446/47).

Закон разведения В. Оствальда. Если в растворе слабых кислот (например, уксусной, щавелевой и т. д.), согласно теории электролитической диссоциации, рядом с не разложенными молекулами находятся ионы, то должно существовать между ними такое подвижное равновесие:

где Z₁Н — какая-либо кислота.

Согласно закону действия масс   (Гульдберга и Вааге) для равновесия

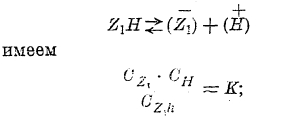
и если

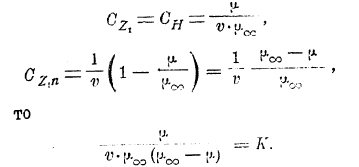
Следующая таблица содержит значения μ_v и μ_∞ для уксусной кислоты:

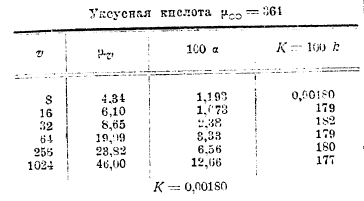
Как видно из таблицы, для разведенных растворов (где v>8) К является величиной очень постоянной. Нужно только отметить, что формула разведения В. Оствальда пригодна только для кислот слабых (органических), степень диссоциации коих мала (см. третий столбец таблицы) и константа К является характерной величиной для данной кислоты, указывающей на особенности состава и строения последней. Для солей же и сильных кислот формула разведения В. Оствальда является совершенно неподходящей. Для таких кислот и солей Рудольфи предложил следующую эмпирическую формулу:

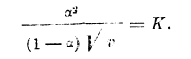
Более подходящей является формула Вант-Гоффа:

так как для многих электролитов К, вычисленная по ней, действительно постоянная величина. Формула Вант-Гоффа показывает, что отношение между концентрацией неразложенных молекул и концентрацией ионов пропорционально расстоянию недиссоциированных молекул.

Электропроводность неводных растворов. Теория электролитической диссоциации создалась и развивалась главным образом на основании изучения свойств водных растворов; по мере же изучения электропроводности неводных растворов она должна была  видоизменяться и дополняться. В 1893 г.   В. Оствальд все сведения об электропроводности неводных растворов мог изложить в своем известном «Handbuch der Allgemeinen Chemie» на 4-х страницах. С тех пор положение вопроса резко изменилось благодаря трудам  многих исследователей (из русских   укажем: П. И. Вальдена, Центнершвера,  А. Н. Саханова, В. А. Плотникова и др.);  собран громадный материал; относительно электропроводности неводных  растворов Томсен и Нернст указали, что на степень электролитической диссоциации влияет диэлектрическая константа (D) растворителя: «диссоциирующая сила» растворителя, т. е. способность его разлагать растворенное тело; тем сильнее, чем больше диэлектрическая константа растворителя (хотя строгой пропорциональности не наблюдается): одна и та же соль в воде (D = 81) диссоциирована в большой степени, в метальном спирте — меньше, еще в меньшей степени в этильном спирте (D = 27). Цианистый водород (HCN) сообразно своей высокой диэлектрической постоянной (D = 97) обладает значительной диссоциирующей способностью. Жидкости с большей диэлектрической постоянной (D = 97) способны разлагать тела с ассоциированными молекулами, например уксусная кислота, пар которой при температурах, лежащих недалеко от точки кипения, содержит около 50% двойных молекул, распадается на простые молекулы при растворении в воде.

Еще в 1900 г. П. И. Вальден показал, что такие минеральные растворители, как РОСl₃, AsCl₃, SO₂, SO₂Сl₂, Н₂SO₄, SbCl₃ и др. вызывают распадение солей на ноны.

Электропроводность растворов в жидком аммиаке подробно изучена Э. Франкликом и Клауссом. М. Центнершвер   в 1902 г. исследовал электропроводность растворов в жидком цианистом  водороде (HСN) и циане (CN)₂. Первый, обладая диэлектрической постоянной (D = 97), превышающей таковую для воды, оказывает сильное диссоциирующее действие, тогда как, второй — с малой диэлектрической постоянной (D=2,5) — оказывает слабодиссоциирующее действие.

П. И. Вальден подверг систематическому исследованию электропроводность растворов в растворителях, принадлежащих различным классам органических тел (см. «Труды Академии Наук СССР») и указал многие закономерности, устанавливающие связь между электропроводностью растворов, диэлектрической постоянной, внутренним трением и т. п. Оказывается, что электролитами являются не только соли, кислоты и основания, но и другие тела; так, П. И. Вальден нашел, что такие тела, как галоиды, фосфор, мышьяк, сурьма, сера, хинолин, пиридин и т. п., образуют растворы в жидком сернистом ангидриде, хлористом сульфуриле и треххлористом мышьяке, обладающие электропроводностью.

Простые законы, установленные для водных растворов солей, большей частью не могут быть применены для растворов во многих других растворителях. Еще в 1889 г. И. А. Каблуковым было указано, что молекулярная электропроводность хлористого водорода в эфире и амильном спирте с разбавлением не увеличивается, а уменьшается, т. е. наблюдается явление, обратное тому, что мы видим для водных растворов. Это явление оказывается общим для всех растворов, образуемых растворителями с малой диэлектрической постоянной: для них уменьшение молекулярной электропроводности с разведением является таким же характерным свойством, как увеличение ее для растворителей с высокими диэлектрическими постоянными.

На электропроводность растворов влияет не только диссоциирующая способность растворителя, но и внутреннее трение (вязкость) последнего; так, например, молекулярная электропроводность многих солей в жидком аммиаке выше таковой в воде, хотя степень диссоциации в последней значительно превышает таковую в аммиаке: в воде степень диссоциации вышеуказанных солей достигает 75% при  v = 5 л, в аммиаке же при v = 350 л и выше.

Большая электропроводность аммиачных растворов объясняется большой подвижностью ионов в аммиаке вследствие того, что вязкость аммиака (η = 2,6 -10^-3) значительно ниже вязкости воды (η = 10,6·10^-3). Меньшая же степень диссоциации аммиачных растворов вполне подтверждает правило Томсена-Нернста: для аммиака D = 21—22, а для воды D = 81.

На основании многочисленных исследований П. И. Вальдену удалось установить следующее соотношение между внутренним трением разбавленного раствора его «нормального электролита» йодистого тетраэтиламмония N(С₂Н₅)I₄J и электропроводностью μ_∞: предельные значения μ_∞ обратно пропорциональны соответствующим коэффициентам внутреннего трения (η”_∞) при 25° и при 0°, Т. е. μ’_∞ : μ”_∞ = η”_∞ : η’_∞ или μ’_∞·η’_∞ = μ”_∞·η”_∞ = const = 0,700. При дальнейших исследованиях П. И. Вальдену удалось доказать применимость этого соотношения для многих бинарных электролитов (солей и нескольких кислот). Оно находит объяснение в предположении, высказанном Кольраушем для водных растворов, а именно: движущийся ион ассоциирован с значительным числом молекул растворителя, вследствие чего он испытывает трение, соответствующее внутреннему трению растворителя.

Теории, объясняющие электропроводность растворов. Когда Вант-Гофф вывел свой закон осмотического давления, устанавливающий аналогию между растворенным и газообразным состоянием тел, то многие исследователи, увлекшись этой аналогией, приняли, что, подобно тому, как в газах давление на стенку сосуда происходит вследствие ударов о стенки сосуда газовых молекул, так и в растворах осмотическое давление вызывается ударами растворенного тела о «полупроницаемую» стенку. Такой взгляд оказал в свое время не малую долю пользы, потому что он позволил перенести многое из того, что было выработано в кинетической теории газов, на явления, совершающиеся в растворах, но такое воззрение устраняло всякое химическое воздействие между растворенным телом и растворителем: последний представлял только среду, в которой молекулы электролита и ионы могли свободно двигаться и своим движением вызывать осмотическое давление и явления, с ним связанные. Но подобный взгляд на природу растворов разделялся не всеми последователями теории Вант-Гоффа и Св. Аррениуса. И. А. Каблуков (1891) в своей докторской диссертации высказал предположение, что при растворении вода разлагает молекулы электролита на ионы, а последние образуют непрочные гидраты. По Чамичану (1890 и 1909) молекулы воды обладают способностью присоединять к себе ионы, причем присоединение происходит так, что анионы оказываются притянутыми к водородным атомам воды, а катионы — к кислородным:

А. Вернер считал, что без гидратации не может быть электролитической проводимости. По Вернеру электролитической диссоциации предшествует химическое взаимодействие растворенного электролита с водой, вследствие которого молекулы воды, внедряясь в молекулы электролита, переводят анионы во вторую сферу катиона; анионы при этом приобретают способность отщепляться от комплексного катиона. Диссоциацию, например, СаСl₂·6H₂O можно изобразить так:

Д. П. Коновалов также указывал, что электропроводность растворов обусловливается явлением химического соединения между растворенным электролитом и избытком растворителя.

Чем больше накапливался фактический материал относительно электропроводности неводных растворов, тем более становилось ясным, что на растворитель нельзя смотреть, как на среду, в которой частицы растворенного тела могут свободно двигаться подобно тому, как газовые частицы в предоставленном им пространстве.

При растворении происходит химическое взаимодействие, более или менее глубоко затрагивающее молекулы растворенного тела и изменяющее их свойства в иных случаях коренным образом. В каждом растворе, как и в определенном химическом соединении, проявляется нечто индивидуальное. В 1900 г. Джонс предложил сольватную теорию растворов, в подтверждение коей привел ряд опытных доказательств.

Основная идея сольватной теории, по коей ионы электролита образуют соединения с молекулами растворителя — гидраты или сольваты, так как не только вода, но и другие растворители способны соединяться с ионами, получила  широкое распространение, и такие авторитеты, как Св. Аррениус и Нернст, признали идею гидратации безусловно правильной.

«Не подлежит никакому сомнению, говорит С. Аррениус, что электролиты соединяются с водой. При увеличении концентрации электролита степень гидратации электролита уменьшается, и тем быстрее, чем значительнее была его гидратация при бесконечном разведении».

По своей способности образовывать гидраты, ионы могут быть расположены в следующий ряд:

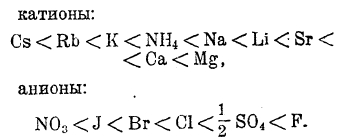
Для катионов имеем следующий ряд гидратированных ионов (в скобках показано число грамм-молекул водорода, соединенных с одним ионом):

Эти числа, данные для разведенных растворов, нужно считать только приблизительными, так как числа, полученные различными методами, не совпадают вполне друг с другом. Для состава сольватов K⁺ и Сl^- в зависимости от растворителя П. И. Вальден дает такие числа:

К. Фаянс принимает, что теплота сольватации ионов является источником энергии для процесса электролитической диссоциации.

Что касается до иона водорода, то нужно принять во внимание, что, согласно электронной теории, водородный атом состоит из атомного ядра и вращающегося вокруг него электрона. При переходе в состояние иона электрон отделяется и, следовательно, водородный ион представляет свободное от электрона ядро чрезвычайно малого диаметра, свободное существование которого в водном растворе невероятно. Благодаря малому размеру, такое ядро может подойти значительно ближе к другим атомам и ионам, чем ионы, обладающие электронной оболочкой, поэтому будет сильно деформировать электронные оболочки других ионов, а также сильно связывать нейтральные молекулы, имеющие дипольный характер, как воду и аммиак. Таким образом, между «протоном» (ядром водорода) и молекулами воды существует сродство. Это сродство Гримм назвал «протонным сродством» и вычислил теплоту присоединения иона водорода к молекуле воды и аммиака, или теплоту образования «гидроксония Н₃O» и «аммония NH₄»: Н₂O + Н⁺ = Н₃O + прибл. 160 больших калорий

NH₃ + Н⁺ = NH₄ + « 196 «  

По мере того, как накапливался опытный материал, подтверждавший основные положения теории С. Аррениуса, накапливались также факты, противоречившие последней. Как и всегда, в начале как бы не замечали подобных фактов, но трудности объяснения новых фактов, согласно теории, все более и более увеличивались и потребовались новые теоретические истолкования явлений электролитической диссоциации. Новые теории (Бьерума, Гоша, Дебая и др.) по мере того, как они стремились обобщить больший круг явлений, все больше удалялись от тех представлений, которые развивал Аррениус, теорию которого в настоящее время (1986) принято называть классической в отличие от новых, появившихся в последнее время.

Основное положение этих теорий заключается в том, что ниже области очень больших концентраций (другие считают, что при любых концентрациях) имеет место полный распад электролита на ионы. Этот взгляд, впервые высказанный Сезерлендом (1902), а после него Герцем (1912), Бьерумом (1918), Гошем, Дебаем и другими, опирается также на термодинамические исследования Льюиса. Казалось бы, что из такого представления неизбежно должно вытекать, что коэффициент і для бинарного электролита равен 2, осмотическое давление вдвое больше нормального и т. д. Но все эти теории учитывают роль электростатического поля ионов; Льюис вводит понятие «активности», показывающее эффективную концентрацию ионов, которая может и не совпадать с аналитической. Благодаря действию электростатических сил, затрудняющих свободное движение ионов и уменьшающих их кинетическую энергию, не все ионы могут себя проявить активно или все ионы не проявляют полной активности. Бьерум, кроме этого, вводит особый коэффициент осмотического давления и электропроводности. Тогда как коэффициент і (теории Вант-Гоффа) дает отношение наблюдаемого понижения точки замерзания к понижению, отвечающему отсутствию диссоциации, осмотический коэффициент f_o (Бьерума) представляет отношение действительного понижения точки замерзания раствора электролита (θ) к ожидаемому при полной диссоциации электролита (θ_∞) и f_o = θ/ θ_∞.

Если n – число ионов, на которые распадается электролит, то f_o = i/n. Для хлористого калия KCl f_o = i/2, для хлористого кальция CaCl₂ f_o = i/3 и т. д.

Интерионные силы являются причиной того, что, несмотря на полную диссоциацию, эквивалентная электропроводность раствора (μ_v) при разбавлении v меньше, чем при бесконечном разбавлении. Коэффициент электропроводности f_o = μ_θ/ μ_∞; как видим, коэффициент электропроводности тождественен со степенью диссоциации классической теории.

Теория Гантча. В связи с изложенным естественно возникает вопрос, как вообще может оправдываться закон разведения В. Оствальда. Как показано выше, он оправдывается для слабых органических кислот. Согласно теории Гантча, эти кислоты существуют в двух формах: истинной кислоты — электролита, и псевдокислоты — неэлектролита:

В первой кислоте атом водорода связан ионогенно, т. е. может отделяться в виде иона (Н₂О), тогда как во второй кислоте атом водорода прочно закреплен внутри молекулы. Между этими кислотами в растворе существует равновесие, сдвигающееся в сторону истинной кислоты по мере разбавления. Это представление Гантча дает возможность, с одной стороны, распространить теорию полного распада электролитов на ионы и на случаи слабых кислот и, с другой стороны, —  понять причину, почему закон разведения приложим в этом случае. Оставаясь на той точке зрения, что электролит диссоциирован нацело, можно принять, что превращение псевдокислоты в истинную, а следовательно, и появление ионов находятся именно в такой зависимости от разбавления, какую нашел Оствальд между степенью диссоциации и разбавлением.

Теория Гантча о существовании псевдоформ охватывает и случаи сильных кислот и щелочей, причем  возникновение истинных кислот считается находящимся в зависимости от образования соединений с водой, что   устанавливает связь увеличения эквивалентной электропроводности с увеличением разбавления. Было бы, однако, неправильным считать, что теория Гантча устраняет все неясности классической теории Аррениуса.

В теории Гоша (Ghosh, 1918) принимается полная диссоциация электролита, и на основании рассмотрения значения электростатической энергии диссоциированного электролита выводятся уравнения для выражения электропроводности как водных, так и неводных растворов. Приведем следующее довольно сложное уравнение, устанавливающее зависимость между электропроводностью и другими свойствами растворов. Для бинарных электролитов:

и для тройных электролитов:

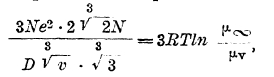
где N — число Авогадро (6,16·10²³), е — заряд одновалентного иона (4,7 Х 10 ^-10 электростатических единиц), D — диэлектрическая постоянная растворителя, v — число литров, в коих находится 1 моль электролита, R - газовая постоянная (8,315 Х 10^-7 С. G. S.).

Не имея возможности входить в более подробное изложение других новейших теорий, мы приведем лишь некоторые из общих результатов работ Дебая-Гюкеля и Онзагера.

Так как в растворе какого-либо электролита катионы и анионы взаимно притягиваются, то они не находятся в состоянии полного беспорядка, характерного для теплового движения молекул идеального газа; поэтому должны наблюдаться отклонения от законов идеально разбавленного раствора. Вблизи какого-либо катиона вследствие электростатического притяжения будут чаще и дольше находиться анионы, чем одноименно заряженные катионы: можно предположить, что катион находится в центре шаровидного облака анионов, которое называют атмосферой иона. Радиус последней зависит от валентности иона, разбавления раствора, температуры, диэлектрической постоянной и т. д. Если в раствор опустить электроды, то катион направится к катоду, а анион к аноду. При этом движении впереди катиона будет образовываться новая ионная атмосфера, тогда как сзади она будет исчезать. Это образование и исчезновение ионной атмосферы требует времени, поэтому анионное облако позади движущегося катиона толще, чем впереди него, а несимметричное расположение анионов вокруг катиона оказывает тормозящее действие на перенос тока. Кроме того, как известно, движение аниона к аноду обусловливает электрический перенос воды к катоду (электроосмос). Оба эти явления служат причиной того, что, несмотря на полную диссоциацию сильных электролитов, их молекулярная электропроводность уменьшается с увеличением концентрации раствора. На основании теоретического обсуждения этих явлений Дебай-Гюкель и Онзагер получили для уменьшения эквивалентной электропроводности (λ_v) с возрастанием концентрации (с) для z-валентного электролита следующее уравнение:

В этом уравнении заключается утверждение, что эквивалентная электропроводность, начиная от бесконечного разбавления, уменьшается линейно от квадратного корня концентрации, - факт, уставленный давно Кольраушем на основании его опытных исследований.

В эмпирической формуле Кольрауша:

множитель b соответствует части, заключенной в скобки уравнения Дебая.

Формулы теории Дебая-Гюкеля правильны только для области разбавленных растворов, причем эта область изменяется в зависимости от природы растворителя: раствор, содержащий 0,01 моля в 1 литре в воде является разведенным, в ацетоне — тоже разведенным, в бензоле же — концентрированным, соответственно обратному отношению к диэлектрической постоянной растворителя (для воды D = 81, для ацетона около 20, для бензола 2). Теория позволяет вывести предельные количественные законы, которые тем более приближаются к данным опыта, чем более разведены растворы, для концентрированных же растворов должны наблюдаться отклонения. Таким образом, разработку теории Дебая-Гюкеля нельзя считать законченной.

В заключение укажем, что основное положение электрохимических теорий Дэви-Берцелиуса, согласно которому электричество является первопричиной химических сил, вполне подтвердилось новейшими исследованиями двадцатого столетия.

Литературу см. при ст. химия, физическая химия (XLV, ч. 2, 332), растворы (XXXV, 692). И. А. Каблуков, «Современные теории растворов Вант-Гоффа и С. Аррениуса, в связи с учением о химическом равновесии» (1891), его же, «Очерк истории электрохимии за XIX век»: его же, «Основные начала физической химии», 2-й вып., Электрохимия; Ле Блан, «Руководство по электрохимии» (перевод с немецкого И. А. Казарновского, 1930); А. Н. Саханов, «Исследования по электрохимии неводных растворов» (1913); его же, «Исследования в области электрохимии» Одесса, 1913 М. А. Рабинович, «Природа электролитической диссоциации» Український Хімічний журнал, т. III, стр. 237—433); В. А. Плотников, «Исследования по электрохимии неводных растворов растворов» (1908), А. И. Бродский, «Современная теория электролитов» (1934), Н. А. Изгарышев, «Электрохимия и ее техническое применение» (1929); W. Ostwald, «Elektrochemie, ihre Geschichte und Lehre»; Sw. Arrhenius, «Lehrbuch der Elektrochemie»; Г. Грубе «Основы теоретической и практической электрохимии», (перевод с немецкого, Ленинград, 1932); Р. Walden, «Elektrochemie nichtwässeriger Lösungen».

Ив. Каблуков.

Электродвижущая сила и электродные потенциалы гальванических элементов. Гальваническими элементами называются приборы, в которых получается электрическая энергия при одновременно совершающихся в них химических процессах (см. гальванизм, XII, 426 сл.). Как пример, можно рассматривать элемент Даниеля, схематически изображенный на рис. 1.

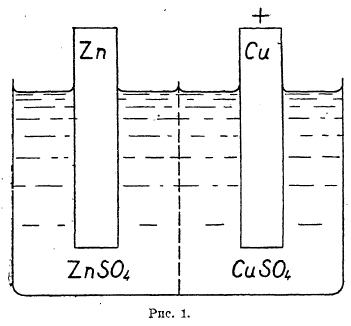
Рис. 1.

В стеклянном сосуде, разделенном пористой перегородкой, в одном отделении находится раствор сернокислого цинка и цинковая пластинка (электрод), в другом — раствор сернокислой меди и медный электрод. При замыкании медного и цинкового электродов проводником по нему начинает течь ток от цинка к меди (по направлению течения отрицательного электричества — электронов). Следовательно, в этом элементе цинк является отрицательным полюсом, а медь положительным.

При работе элемента можно обнаружить, что цинк переходит в раствор в виде ионов, т. е. на цинковом электроде совершается химический процесс:

а на медном электроде выделяется металлическая медь, т. е. совершается процесс:

При переходе одного грамм-эквивалента цинка в ионное состояние и такого же количества ионов металлическое состояние через внешнюю цепь элемента протекает 1F (96 500 кулонов) электричества. Таким образом, электрохимические процессы, совершающиеся в гальванических элементах, протекают в соответствии с законом Фарадея, и количество электричества, полученное от элемента (емкость элемента), будет пропорционально количеству веществ, испытавших химическое превращение на электродах. Электродвижущая сила (сокращенно эдс) элемента есть разность потенциалов, существующая между его электродами, т. е.:

Изучение электродвижущих сил и электродных потенциалов элементов имеет большое значение: оно дает представление о количестве энергии, обращенной в работу при электрохимических процессах, об условиях возникновения этих процессов, а также о   процессах разряда и образования ионов   на электродах и, наконец, о порядке,   в котором происходит разряд ионов в  случае одновременного присутствия   нескольких ионов в растворе.

Реакции, совершающиеся в элементе Даниеля, суммарно могут быть представлены в виде уравнения:

и осуществлены, если просто кусок  цинка погрузить в раствор сернокислой меди, с тем лишь отличием, что при этом электрическая энергия  не образуется, а имеет место выделение некоторого определенного количества тепла Q, равного 50 110 калорий, если превращению подвергнется один грамм-атом цинка. Поэтому Томсон предположил, что теплота реакции, осуществляемой таким образом, эквивалентна тому количеству электрической энергии, которое может быть получено в элементе Даниеля при переходе соответствующего количества цинка с цинкового электрода в раствор в виде ионов, т. е., принимая во внимание, что 0,239 кал. = 1 вольт х 1 кулон, имеем:

Эдс элемента Даниеля, вычисленная на основе предположения Томсона, как и во многих других случаях, дает величину, удовлетворительно совпадающую с непосредственно измеренной. Однако, наблюдаются и большие отклонения, и таким образом предположение Томсона неверно.

Действительно, как показал Гельмгольц, при всяком химическом процессе только часть общего изменения энергии системы может быть превращена в другой вид энергии, например в электрическую. Эту часть Гельмгольц назвал свободной энергией. Остальная часть обязательно проявится как тепловая энергия, т. е. имеет место равенство:

Q = А + q,

где Q — общее изменение энергии системы, А — свободная энергия и q — тепловой эффект процесса.

В дальнейшем Гиббс и Гельмгольц установили связь между свободной энергией процесса и общим изменением энергии системы в виде уравнения:

где Т - абсолютная температура, при которой совершается процесс. При этом следует оговориться, что уравнение это справедливо лишь для систем, в которых протекают обратимые процессы. Элемент Даниеля как раз относится к типу обратимых. Действительно, если извне приложить к нему эдс внешнего источника постоянного тока, приключив отрицательный полюс последнего к цинковому электроду, то начнется выделение металлического цинка на цинковом электроде и переход меди с медного в виде ионов в раствор, т. е. процесс будет протекать в направлении, обратном совершающемуся при работе элемента. Поэтому для элемента Даниеля справедливо будет соотношение:

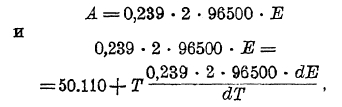
В общем же виде, когда моль, равный n эквивалентам вещества, химически превращается в гальваническом элементе, то:

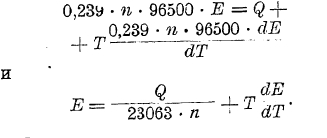
Из последнего уравнения следует, что предположение Томсона справедливо лишь тогда, когда dE/dT = 0, т. е. когда эдс  элемента не изменяется с изменением температуры. Экспериментальное подтверждение справедливости уравнения Гиббса-Гельмгольца было дано Яном и Бугарским.

Возникновение потенциала или, точнее, разности потенциалов между металлом и раствором его соли, в который металл погружен, было разъяснено Нернстом в созданной им «Осмотической теории гальванических элементов». Согласно Нернсту, каждому металлу присуща электрическая упругость растворения, т. е., стремление атомов металла перейти в раствор в виде ионов. Сила этого стремления различна для различных металлов, т. е., помимо природы растворителя, она зависит от природы металла. Противодействие проявлению этой силы возникает со стороны ионов металла, уже присутствующих в растворе и образовавшихся путем диссоциации соли металла, и оно  пропорционально их осмотическому давлению Р, а следовательно их концентрации.

Если электролитическая упругость растворения металла P_Met больше, чем осмотическое давление ионов металла в растворе, в который металл погружен, то будет иметь место процесс:

причем электроны будут оставаться на металле, а положительно заряженные ионы металла перейдут в раствор. Переходящие под действием электролитической упругости растворения ионы не могут продиффундировать от поверхности металла вглубь раствора, т. к. они удерживаются силами электростатического притяжения, возникающими между ними и отрицательно заряженным металлом.

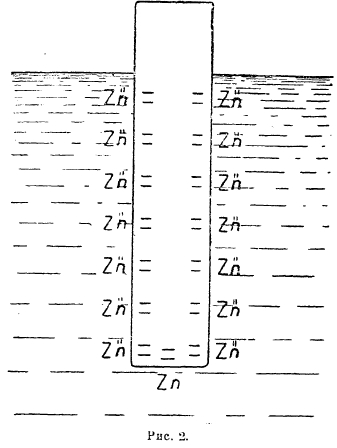
Рис. 1.

Поэтому на границе металл-раствор возникнет двойной электрический слой (рис. 2), т. е. между металлом и раствором возникнет разность потенциалов: металл приобретет относительно раствора какой-то потенциал, величина которого зависит от соотношений P_Met и р. Полагая, что переход металла с электрода в раствор в виде ионов подобен процессу изотермического расширения газов, максимальная работа при котором для моля газа выражается уравнением:

где R — газовая постоянная, Р₁ — исходное давление газа и Р₂ — конечное, Нернст положил, что электрическая работа, совершаемая при переходе одного грамм-атома металла с электрода в раствор, выразится аналогичным уравнением:

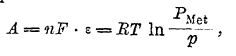
где n — валентность металла и  ε — потенциал, приобретенный им относительно раствора. Выражая в этом уравнении R в электрических единицах (R = 8316 вольт-кулонов) и вводя для перехода от натуральных логарифмов к десятичным модуль = 0,4344, получаем:

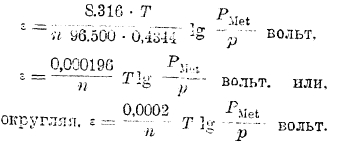
Принимая во внимание, что если Р_Met > р, то электрод относительно раствора зарядится отрицательно и, следовательно, потенциал электрода будет отрицательной величиной, то, чтобы из уравнения получить не только величину, но и знак потенциала, окончательно пишем:

Экспериментальная  проверка уравнения Нернста может быть произведена путем измерения эдс так называемых «концентрационных цепей» и сравнения ее с вычисленной.

Примером концентрационной цепи может быть цепь, построенная из двух серебряных электродов, опущенных один в раствор азотнокислого серебра с концентрацией Ag, равной С₁, и второй в раствор, где концентрация ионов серебра С₂, причем растворы находятся в соприкосновении:

Так как осмотическое давление ионов серебра, находящихся в растворе, может быть выражено в зависимости от их концентрации уравнением р = RTC, то потенциалы электродов выразятся уравнениями:

а эдс построенной цепи – уравнением

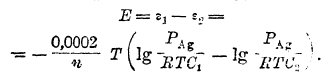
После преобразования имеем:

Из полученного уравнения легко может быть вычислена эдс такой пары, причем легко сообразить, что положительным полюсом в ней будет электрод, погруженный в раствор, в котором концентрация ионов металла больше.

Результаты, полученные Аббегом и Куммингом для таких цепей, представлены в нижеследующей таблице:

Как видно, совпадение вычисленных и экспериментально найденных величин вполне удовлетворительное, что служит непосредственным подтверждением справедливости уравнения Нернста.

Газовые электроды. Переходить в ионное состояние способны не только металлы, но и вещества, обычно существующие в газообразном состоянии, как водород, хлор и т. д. Однако, в этом случае процесс ионообразования будет несколько сложнее, т. к., например, чтобы перейти в ионное состояние

молекула водорода должна лишиться двух электронов. Этот процесс оказывается возможным в том случае, если, с одной стороны, газообразный водород соприкасается с раствором, содержащим ионы водорода, и с другой — с проводником первого рода, неспособным к самостоятельному новообразованию — с индифферентным электродом. Последними, в случае водорода, например, могут быть уголь, платина, золото. В таком случае процесс перехода водорода в ионное состояние будет совершаться, а индифферентный электрод за счет оставляемых на нем водородом электронов зарядится до некоторого потенциала. Последний, однако, зависит не только от концентрации в растворе ионов водорода, противодействующих переходу водорода в ионное состояние, но и от давления, под которым находится газообразный водород. Переход газообразного водорода в ионное состояние будет совершаться в тем большей степени, чем под большим давлением он находится. Так как из молекулы водорода образуются два иона, то потенциал индифферентного водородного электрода в таком случае выразится уравнением:

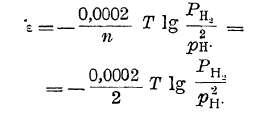
Это уравнение может быть преобразовано следующим образом:

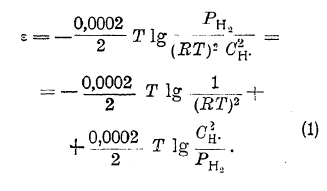
Так как осуществление электрода, между которым и соприкасающимся с ним раствором не существовала бы разность потенциалов, т. е. электрода с потенциалом, равным нулю (нулевой электрод), встречает ряд принципиальных затруднений, то по предложению Нернста электродом, потенциал которого условно считают равным нулю, принят нормальный водородный электрод, т. е. индифферентный электрод, окруженный в верхней части газообразным водородом под давлением, равным одной атмосфере, и погруженный в раствор, в котором концентрация ионов водорода равна одному грамм-иону в литре. Потенциалы электродов, величина которых дается по водородному электроду, т. е. принимая потенциал нормального водородного электрода равным нулю, обозначаются обычно знаком ε_h . Тогда потенциал водородного электрода, у которого давление газообразного водорода равно P_atm, а концентрация ионов водорода соответственно равна С_н, выразится уравнением:

т. к. в уравнении (1) для нормального водородного электрода второе слагаемое обращается в нуль, а первое принимается равным нулю.

Из последнего уравнения видно, что потенциал водородного электрода будет тем более отрицательным, чем выше давление газообразного электрода и меньше концентрация ионов водорода в растворе.

Если принять во внимание, что при процессе

потенциал хлорного электрода будет тем более положительным, чем больше хлора перейдет в ионное состояние, то очевидно, что потенциал хлорного электрода может быть выражен уравнением:

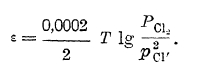
Переход кислорода в ионное состояние, если растворителем, с которым соприкасается индифферентный электрод, является вода, происходит несколько сложнее, а именно:

и противодействие переходу кислорода в ионное состояние будут оказывать гидроксил-ионы. Поэтому потенциал кислородного электрода выразится уравнением:

Окислительно-восстановительные потенциалы. Так как причиной возникновения разности потенциалов между электродом и раствором является возможность процесса, в результате которого на электроде или остаются избыточные электроны,: или они забираются с него, то возможен еще один вид процессов, в результате которых электрод приобретает  некоторый потенциал относительно раствора.

Процессы окисления и восстановления ионов, как то:

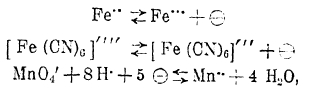
сопровождающиеся в зависимости от направления их течения отдачей или  восприятием электронов, очевидно  могут послужить причиной возникновения потенциала на индифферентном  электроде, погруженном в среду, содержащую вещества, указанные в приведенных химических уравнениях. Действительно, это и наблюдается, причем, как не трудно сообразить, потенциал электрода становится тем более положительным, чем выше концентрация в растворе ионов с более высокой степенью окисленности и ниже концентрация ионов менее окисленных.

Величина потенциала индифферентного электрода, погруженного в растворы смесей указанных выше веществ (окислительно-восстановительный потенциал), может быть выражена уравнениями:

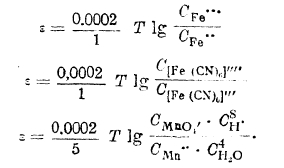
Нормальные потенциалы и электрохимический ряд напряжений. Ранее данное уравнение потенциала металла относительно раствора его соли путем замены величины осмотического давления ионов металла через выражение С = RТС может быть преобразовано в двухчленное, как это было сделано для водородного элемента:

В этом уравнении второй член, если концентрация соответствующих ионов равна одному грамм-иону на литр, обращается в нуль. В первом члене неизвестной величиной будет P_Met —  электролитическая упругость растворения металла, так как ее непосредственно нельзя измерить или вычислить. Но если соединить полуэлемент Met|_c^Met· в пару с нормальным водородным электродом, то, измерив эдс полученного элемента, можно найти численное значение потенциала металла для этого случая. Этот потенциал металла относительно раствора, в котором концентрация ионов металла равна 1 г ион/лит., называется нормальным потенциалом металла и обозначается через ε_h°. Тогда уравнение потенциала металла при любой концентрации его ионов в растворе приобретет вид:

и потенциал металла может быть вычислен, если известна температура раствора и концентрация в нем ионов металла. Для газового электрода таким же образом может быть определен нормальный потенциал лишь с дополнительным условием, что давление газа при этом равно одной атмосфере. И тогда, например, для хлорного электрода, получаем уравнение:

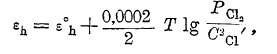
пользуясь которым можно вычислить потенциал хлорного электрода при любом давлении газообразного хлора и любой концентрации ионов хлора в растворе. Такую же величину нормального потенциала можно ввести и для   окислительно-восстановительного электрода, понимая под ней потенциал  индифферентного электрода в растворе, в котором концентрация каждого электрохимически активного вещества  равна 1 гр.-иону/литр. Тогда потенциал окисно-закисного железа выразитcя уравнением:

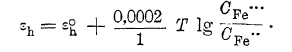
Ниже дана таблица нормальных потенциалов, обычно называемая «электрохимическим рядом напряжений».

Электрохимический ряд напряжений.

Необходимо отметить, что согласно теории полной диссоциации сильных электролитов в уравнения потенциалов Нернста следует ставить на место концентрации ионов соответствующую им при этой концентрации «активность», или умножать концентрацию на коэффициент активности: f_a = а/с где а — «активность» и с — концентрация ионов. Для зависимости активности от диэлектрической постоянной растворителя, температуры, концентрации и зарядности ионов Шередом было выведено соответствующее уравнение. Соответственно и нормальными потенциалами в этом случае будут потенциалы не при концентрации ионов, равной единице, а при активности их, равной единице, но они мало отличаются от вышеприведенных в таблице.

Следует отметить, что в гальванической паре есть еще одно место, где может возникнуть разность потенциалов — это граница соприкосновения двух растворов. Действительно, если соприкасаются, например, два раствора НСІ: 0,1n и 0,01n, то при процессе диффузии из первого раствора во второй первыми, как обладающие большой подвижностью, будут проникать ионы водорода. Хотя вследствие наличия сил электростатического взаимодействия они не могут уйти от ионов хлора, но все же одна сторона границы соприкосновения слоя концентрированного и разбавленного электролита будет иметь повышенную концентрацию положительно заряженных ионов водорода, а другая — отрицательно заряженных ионов хлора, т. е. на границе возникнет разность потенциалов. В таком случае величина разности потенциалов, возникающая за счет разности в скоростях диффузии анионов и катионов и называемая «диффузионной разностью потенциалов», согласно Нернсту будет выражаться уравнением:

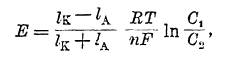
где I_A и І_к — подвижности аниона и катиона электролита. Эту разность потенциалов приходится иногда учитывать при измерениях эдс гальванических пар. Чаще же ее стараются уничтожить, вставляя между такими растворами концентрированный раствор  электролита, у которого ионы обладают  приблизительно одинаковой подвижностью (например, KCl, KNO₃). Тогда при   диффузии этого электролита в оба   боковых раствора, как не трудно сообразить, диффузионной разности потенциалов не возникает. Как видно из  ряда напряжений, нормальные потенциалы металла относительно ионов различной валентности различны. Связь между величиной этих потенциалов и потенциалом перехода иона высшей валентности в низшую была установлена Лютером. При обратимо протекающем процессе работа процесса не зависит от пути, а лишь от начального и конечного состояния системы. Поэтому если процесс протекает электрохимически и:

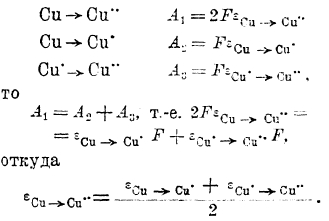
Следует, однако, иметь ввиду, что, например, при наличии в растворе ионов закисного и окисного железа в присутствии металлического железа должно иметь место химическое равновесие:

а последнее возможно при условии, что:

т. е. при определенном соотношении ионов окисного и закисного железа. Если в исходном растворе этого не было, возникнет процесс, протекающий в определенном направлении. Поэтому при введении в раствор соли окиси железа металлического железа она почти целиком превращается в соль закиси, т. к. равенство потенциала железа относительно окисных и закисных ионов последнего может установиться  лишь при весьма малой концентрации ионов Fe^··· и весьма высокой концентрации ионов Fе^··.

Напряжение разложения электролитов и электродные процессы при электролизе. Если два медных электрода погружены в раствор какой-нибудь медной соли (например, CuSO₄), то при приключении к электродам внешнего источника постоянного тока прохождение тока начинается уже при ничтожно малой разности потенциалов. Сила тока с возрастанием извне приложенного напряжения возрастает пропорционально последнему (во всяком случае, при низких плотностях тока), и зависимость этих двух величин может быть выражена прямой линией (рис. 3), наклон которой к оси абсцисс зависит от концентрации электролита, расстояния между электродами и их поверхности, иначе говоря, от сопротивления столба электролита, заключенного между электродами.

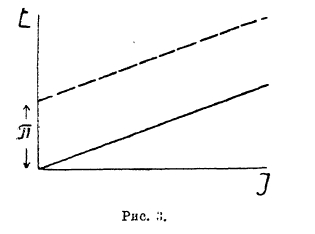
Рис. 3.

Таким образом, оказывается, что к этому случаю вполне применим закон Ома: Е = IW, где Н — разность потенциалов между электродами, I — сила проходящего через электролит тока и W — сопротивление электролита. Что такая зависимость в этом случае должна наблюдаться, вытекает из следующих рассуждений. До электролиза оба электрода обладали одинаковыми потенциалами  ε, т. к. на обоих имело место равновесие   вследствие одинаковой концентрации ионов у электрода, ибо они были погружены в один и тот же раствор. Приключив к аноду положительный полюс, мы вызвали уход части электронов с электрода во внешнюю цепь. Потенциал электрода поэтому сделался положительнее на какую-то величину  Δε и вследствие нарушения равновесия начался процесс

Обратно  приключив отрицательный полюс внешнего источника тока к катоду, мы подвели к электроду дополнительное количество электронов, что вызвало изменение потенциала электрода на величину — Δε и, вследствие нарушения равновесия, пошел процесс

Таким образом, если у нас через такую систему протекает ток силой J амп. при сопротивлении электролита равном W Ом, то падение напряжения в участке цепи анод-электролит—катод будет равно:

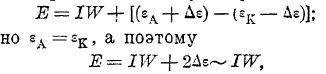
т. к. при малой силе тока величина Δε (что на самом деле и имеет место) настолько мала, что ею можно пренебречь.

Как дополнительное следствие, из всех этих рассуждений вытекает, что потенциал разряда катиона будет всегда более отрицателен, чем потенциал равновесия, а потенциал образования его более положителен.

Путем аналогичных рассуждений относительно электрода, на котором образуются анионы (например, ), можно заключить, что потенциал разряда аниона более положителен, чем потенциалы равновесия, а потенциал образования более отрицателен.

Введя понятие потенциал разряда иона, легко истолковать явления, наблюдающиеся, например, при электролизе раствора CuCl₂, если в отличие от предыдущего случая анодом взять графитовую пластинку, т.  е. исключить возможность образования катионов на аноде при электролизе. Тогда зависимость между напряжением и силой тока выразится тоже прямой линией, но выходящей не из начала координат, а отсекающей на оси ординат какое-то первоначальное напряжение  π, при достижении которого лишь может начаться электролиз (рис. З). Это напряжение, ниже которого электролиз не имеет места, называется «напряжением разложения» данного электролита. Зависимость между напряжением и силой тока в этом случае уже выразится уравнением:

Е = IW + π. Величина π по предыдущему, очевидно, может быть выражена уравнением:

Но в данном случае ε_A = ε_к, т. к. на катоде при электролизе здесь выделяется медь, а на аноде — газообразный хлор при соответствующем потенциале разряда ионов хлора. Таким образом, очевидно, что напряжение разложения есть разность потенциала разряда аниона и катионов, имеющая место при таком виде электролиза — с нерастворимым анодом.

Исследование напряжений разложения водных растворов целого ряда электролитов было произведено Лебланом и привело к весьма важным для теории электролиза следствиям. Ряд значений полученных нм, дан в нижеследующей таблице: 

Напряжение разложения водных растворов электролитов.

Из данных таблицы первым долгом обращает на себя внимание практически одинаковое напряжение разложения кислородных кислот и щелочей. В то же время оно практически не зависит от их концентрации, а напряжение разложения НСl возрастает с разбавлением и в разбавленных растворах становится равным тому, которое наблюдается для кислородных кислот и щелочей. Это же имеет место и для НВr.

При электролизе водных растворов кислородных кислот и щелочей на катоде выделяется водород, а на аноде кислород; при электролизе же концентрированных растворов НСl на аноде выделяется хлор, и лишь в разбавленных растворах, когда напряжение разложения станет равным напряжению кислородных кислот, этот процесс сменяется выделением кислорода. На основе этого Леблан пришел к заключению, что если при электролизе водных растворов электролитов на аноде выделяется кислород, а на катоде водород, то это является следствием разряда Н' и ОН'. Электролиз в таком случае происходит за счет разряда ненов воды, т. е. здесь наблюдается первичное разложение, воды. Это вполне подтверждается практически одинаковым напряжением разложения водных растворов Сd(NO₃)₂ и CdSO₄, т. к. это есть следствие тождественности катодного

 и анодного   процессов.

На основе понятия «потенциал разряда иона» понятно также соотношение напряжений разложения Pb(NO₃)₂ и AgNО₃, т. к. при равенстве анодного   потенциала, требующегося на происходящий в обоих случаях разряд ОН', при концентрации ионов свинца равной концентрации Ag^· потребуется для разряда его ионов более электроотрицательный потенциал, что и вызывает  для Pb(NO₃)₂ большую величину напряжения разложения сравнительно с  AgNO₃.

Из всего предыдущего следует, что на катоде при отсутствии каких-либо  осложнений будут разряжаться катионы, требующие для этого наименее отрицательного потенциала, а на аноде — анионы с наименее положительным потенциалом разряда.

Поэтому, если приготовить раствор, содержащий CdCl₂ и ZnBr₂, то при электролизе с малой силой тока на аноде будет выделяться бром, а на катоде кадмий, т. к. эти ионы дают пару с наименьшим напряжением разложения.

Поляризация. Потенциал катодного разряда или анодного образования ионов металла практически совпадает с потенциалом равновесия, но это наблюдается лишь при весьма малых силах тока. При повышении плотности тока наблюдается заметное отклонение потенциала электрода от этого значения, и отклонение тем больше, чем выше плотность электролизирующего тока.

Рис. 4.

Кривые зависимости степени отклонения потенциала от плотности тока для анода и катода – степень поляризации электродов – имеют вид, подобный изображенному на рис. 4 (Ia  и k). Как видно, потенциал катода с повышением плотности тока постепенно становится отрицательнее, а потенциал анода — положительнее. Причина такого хода изменения потенциала катода заключается в том, что по мере разряда катионов слой раствора, прилегающий к катоду, обедняется ионами металла, т. к. в силу недостаточной скорости диффузии убыль их в катодном слое не успевает восполняться. Понижение же концентрации ионов металла в растворе, находящемся в соприкосновении с металлом, как следует из уравнения Нернста, вызывает смещение значения потенциала к более отрицательным значениям. Обратно, в анодном пространстве при электролизе концентрация ионов металла повышается, т. к. они не успевают отдиффундировать, а поэтому потенциал анода изменяется в сторону более положительных значений.  Так как с повышением температуры скорость диффузии увеличивается, то и поляризация электродов при этом уменьшается. Этот вид поляризации, возникающий из-за недостаточной скорости диффузии ионов  и поэтому носящий наименование диффузионной поляризации, тем  сильнее выражен, чем выше плотность  тока и ниже концентрация раствора. Ясно также, что диффузионная поляризация может быть практически уничтожена энергичным перемешиванием раствора.

Однако, помимо наличия лишь только диффузионной поляризации, что имеет место, например, при электролизе Pb(NO₃)₂, AgNO₃ и CuSO₄, в целом ряде случаев  имеет место сильная поляризация электродов, которая не уничтожается перемешиванием (рис. 4, II а и к). Это имеет место, когда электровыделение металла происходит из комплексной соли, в которой металл входит в комплексный ион. Что поляризация здесь весьма значительна, видно из данных  нижеследующей таблицы.

Так как в растворе имеет место равновесие , которое при электролизе нарушается, причем в катодном пространстве вследствие разряда ионов металла происходит реакция, протекающая слева направо, а в анодном вследствие образования ионов металла — справа налево, то ясно, что концентрация ионов в слоях электролита, прилегающего к электродам, будет зависеть от скорости соответствующих химических процессов. Если скорость процесса недостаточно велика по сравнению со скоростью разряда или образования ионов, то будет иметь место изменение концентрации последних в католите и анолите, что и вызовет поляризацию электродов. Здесь поляризация возникает из-за недостаточной скорости химических процессов, и она, по предложению Ферстера, названа «химической поляризацией».

Рис. 5

Химическая поляризация наблюдается и в случае электролиза простых солей таких металлов, как, например, Ni, Со, Fe, что, по мнению Леблана, объясняется недостаточной скоростью дегидратации или гидратации соответствующих ионов, т. е. реакциями:

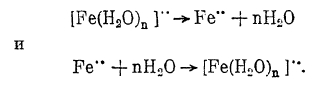
Так как скорость химических процессов сильно возрастает с повышением температуры, то соответственно этому и степень химической поляризации при этом резко снижается.

Перенапряжение. Потенциал обратимого выделения водорода легко вычисляется из уравнения

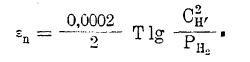
Однако, это имеет место лишь на платиновом или платинированном электроде. На электродах из других металлов, как видно из рис. 5, выделение водорода сопровождается сильной поляризацией, степень которой и выражается уравнением η = a – b ln D_k,  и  зависит от плотности тока D_k. Но в первую очередь перенапряжение определяется металлом, из которого сделан электрод. Это явление носит название «перенапряжения» (иногда  «сверхнапряжения») и объясняется по разному. Одни, как Тафель, видят причину этого в недостаточной скорости процесса перехода атомарного водорода в молекулярный: 2Н → Н₂, по различному катализируемого различными металлами-электродами. Другие, как Эрдей-Грунц и Фольмер, видят причину перенапряжения в недостаточной скорости процесса разряда ионов водорода

Явление перенапряжения наблюдается также и при анодном выделении кислорода или хлора. Металлы по степени перенапряжения на них этих веществ образуют ряды, индивидуальные для каждого из газов и отличные от наблюдаемого для водорода.

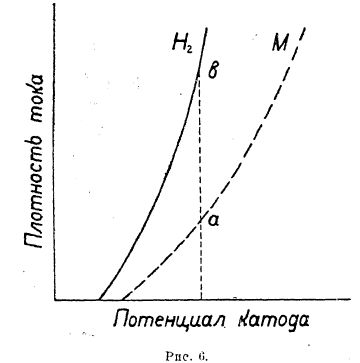
Рис. 6.

В том случае, если поляризация при выделении какого либо металла и перенапряжение водорода на этом металле по величине мало различаются друг от друга, то при наличии в растворен ионов и ионов металла наблюдается совместное выделение и металла и водорода на катоде. Соотношение количеств выделяющихся металла и водорода зависит от относительного расположения поляризационных кривых. Из рис. 6 и 7 видно, что в первом случае будет с повышением плотности тока возрастать количество выделяющегося водорода (b—а) и во втором металла.

Электровосстановление и электроокисление при электролизе. Помимо процессов, заключающихся в изменении заряда иона, как, например:

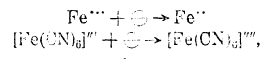
протекающих с более или менее заметно выраженной поляризацией на катоде, при электролизе возможны процессы электровосстановления путем взаимодействия вещества, присутствующего в растворе, с атомами водорода, образующимся при разряде Н^·. Примером этого является восстановление иона азотной кислоты в азотистую  или восстановление нитробензола в анилин:

Рис. 7.

Следует отметить, что восстановление будет происходить лишь при возможности создания соответствующего потенциала на электроде. Если же водород сможет выделяться при более низком потенциале, то он будет удаляться в виде газа, не производя восстановления. Точно так же, если при некотором потенциале катода возможно произвести восстановление частично (например, нитробензола лишь до азобензола), то при более отрицательном потенциале будет образовываться более восстановленный продукт (например, анилин из нитробензола). Кроме того, следует подчеркнуть, что помимо влияния величины потенциала имеет большое  значение и каталитическое действие   металла электрода. Азотная кислота  на железном электроде восстанавливается лишь до азотистой, а на медном до аммиака.

Процессы анодного окисления имеют  полную аналогию с электровосстановлением, т. е. возможны процессы:

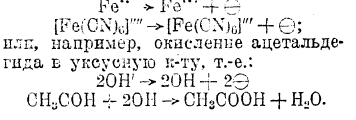
Интересны также процессы образования надкислот путем соединения нескольких частично разреженных ионов:

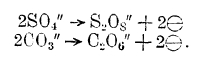
Так можно получать электролизом соли надсерной, надугольной, надфосфорной  и др. надкислот.  

Литература: K. Kremann und K. Müller, «Elektromotorische Kräfte, Elektrolyse und Polarisation». Teil I-II.

П. Титов.