Эллиптические функции

Эллиптические функции, группа специальных функций, появившаяся в математическом анализе в связи с т. н. эллиптическими интегралами. Из интегрального  исчисления известно, что интеграл вида

где R знак рациональной функции, а Р(х) - многочлен, выражается через т. н. элементарные функции (к ним принадлежат — рациональная, иррациональная, показательная, логарифм и тригонометрические) лишь в том случае, если степень Р(х) будет не выше второй; если же Р(х) многочлен более высокой степени, то такое интегрирование, вообще говоря, невозможно. К этой категории принадлежит в частности интеграл, выражающий длину дуги эллипса:

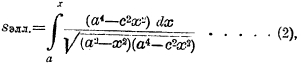
т. к. содержит корень квадратный из многочлена 4-й степени. В связи с этим название эллиптических получили все интегралы вида (1), когда Р(х) многочлен 3-й или 4-й степени (один случай переходит в другой помощью замены переменной), не имеющий кратных корней; в этом последнем случае интегрирование оказывается выполнимым, и интегралы будут псевдоэллиптическими. Если степень Р(х) выше 4-й, мы имеем гипер- или ультраэллитпические интегралы. Интегралы вида (1)  являются частным случаем более общих абелевых интегралов — ∫R (х, у) dx, где у — алгебраическая функция, т. е. функция, определяемая уравнением f (х, у) = 0, в котором f — целая функция.

Эллиптические интегралы, как не выражающиеся через элементарные функции, следует рассматривать как новые трансцендентные функции и, для того чтобы иметь возможность ими практически пользоваться (а с эллиптическими интегралами пришлось встретиться, в целом ряде вопросов), оказалось необходимым составить с достаточной точностью таблицы их числовых значений. Задача эта была выполнена (путем разложения подынтегральной функции в бесконечный ряд) Лежандром (см.), исследовавшим новые функции (1825—28) и показавшим, что все эллиптические интегралы могут быть сведены к 3 стандартным формам, из которых более важными являются интегралы I и II рода:

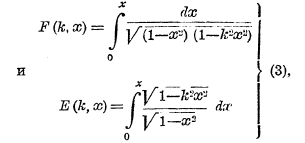
или в эквивалентной тригонометрической форме (после подстановки x = sin φ):

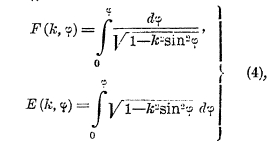
где модуль k — правильная дробь, а амплитуда φ меняется от —π/2 до +π/2. Интеграл  F, взятый в пределах от 0 до π/2, называется полным и обозначается K; если модуль к заменить на k' = √1—k², то соответствующий полный интеграл обозначается K’. Лежандром были составлены обширные числовые таблицы интегралов I и II рода, легшие в основание всех современных таблиц. Обычно полагают k = sin φ и значения эллиптических интегралов располагают в виде таблицы с двойным входом, где θ и φ меняются в пределах от 0° до 90°.

Эллиптические интегралы в их алгебраической форме обладают, как показали дальнейшие исследования, рядом важных функциональных свойств, и, в частности, эллиптический интеграл I рода, рассматриваемый в области комплексного переменного, имея для х = ±1 и х = ±1/k критические точки, обладает двумя полярными периодами и является т. о. функцией бесконечно - многозначной, подобно функции arcsin x, в которую он и переходит в предельном случае k = 0. И подобно тому, как удобнее иметь дело не с многозначной функцией — арксинусом, а с обратной ей однозначной функцией sin х, оказывается целесообразным от многозначных эллиптических интегралов перейти к функциям им обратным. Эта чрезвычайно плодотворная мысль об обращении эллиптических интегралов принадлежит Абелю (1823) и Якоби (1827), пришедшим к ней независимо друг от друга (еще ранее этим вопросом занимался Гаусс). Обращение эллиптических интегралов и приводит нас к эллиптическим функциям.

В интеграле I рода

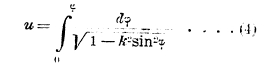
нужно рассматривать верхний предел, амплитуду φ, как функцию от значения интеграла u:

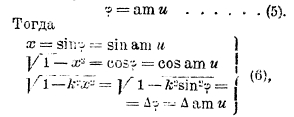
что теперь записывается короче:

При этом x = sn u, являющийся верхним пределом эллиптического интеграла I рода в его алгебраической форме, оказывается, так же как и две другие функции, однозначной аналитической функцией u. Следует притом отметить, что такое обращение является возможным лишь для эллиптических интегралов; если степень Р(х) выше 4-й — однозначность нарушается. Полное доказательство этих предложений сделалось возможным лишь с дальнейшим развитием теории функций комплексного переменного (Лиувилль, Эрмит, см.).

Три функции sn u, cn u и dn u получили название якобиевых эллиптических функций. При k = 0 sn u и cn u переходят в обычные тригонометрические функции синус и косинус, а dn u в 1. Функции эти, подобно тригонометрическим, периодичны, но в отличие от них обладают двумя независимыми периодами (отношение которых мнимое). Аналогия с тригонометрическими функциями может быть продолжена и далее. Для эллиптических функций существуют также формулы сложения и приведения: sn (u + v) рационально выражается через sn u, сn u, dn u и sn v, cn v и dn v; если аргумент и увеличивается на величину полного интеграла K, sn u переходит в простую функцию от сn u и dn u, при прибавлении к аргументу 2K—sn u меняет только знак, 4K является т. о, периодом для sn u; вторым периодом служит 2іK' (то же с соответственными видоизменениями относится и к другим эллиптическим функциям). Sn u оказывается нечетной функцией, а сn u (и dn u) четной. Наряду с двоякопериодичностью функции Якоби обладают другим важным с точки зрения теории функций свойством — все они имеют полюсы (1 порядка) и, не имея других особенных точек, суть, следовательно, функции дробные (мероморфные).

Абель и Якоби ввели также в рассмотрение особую целую трансцендентную функцию θ (встретившуюся уже ранее Фурье), определяемую при помощи бесконечного, весьма быстро сходящегося степенного ряда. Кроме этой первой функции тэта, Якоби ввел в дальнейшем еще три других функции тэта и положил их в основание всей теории эллиптических функций Sn u, cn u и dn u весьма просто выражаются через частные функций тэта. Все функции тэта очень удобно выражаются через хорошо сходящиеся тригонометрические ряды и играют значительную роль в приложениях эллиптических функций.

Дальнейшее развитие теории эллиптических функций связано с именем Вейерштрасса (см.). С точки зрения Вейерштрасса, легшей в основу современной теории функций, функция определяется не внешним, формальным заданием, а своими особенностями. Такими характерными свойствами для эллиптических функций являются обладание периодами и полюсами. В современном анализе эллиптической функцией называется всякая двоякопериодическая мероморфная функция, т. е. функция, во-первых, удовлетворяющая равенствам

8, где ω₁ и ω₂ — периоды, отношение которых мнимое (двух периодов, отношение которых было бы числом вещественным, а также более двух периодов однозначная функция — как показал Якоби — иметь не может), и, во-вторых, не имеющая других особенностей, кроме полюсов (периодическая функция, которая не имела бы совсем особых точек, целая, была бы всюду ограниченной и в силу т. н. теоремы Лиувилля должна была бы сводиться к постоянному). Определенные т. о.   эллиптические функции обладают, как показали работы Лиувилля (1841), рядом важных свойств. Число нулей эллиптических функций в параллелограмме периодов равно числу полюсов и не может быть меньше двух. Число это называется порядком эллиптических функций. Эллиптические  функции n-го порядка принимает в параллелограмме периодов каждое значение n раз. Две эллиптические функции, имеющие одинаковые периоды и полюсы с одинаковыми бесконечными частями, отличаются лишь на постоянное слагаемое. Эллиптические  функции этими данными т. о. вполне определяется.

Вейерштрасс (1840) и поставил перед собой задачу построить эллиптические функции по данным периодам и полюсам, приняв за простейшую эллиптическую функцию, функцию, имеющую 1 двойной полюс в точке ω = m₁ω₁ + m₂ω₂, где ω₁ и ω₂ - выбранные произвольно периоды (с тем только ограничением, что ω₁/ω₂ — число мнимое). Как получить такую функцию? Если взять элементарную (целую) функцию sin u, имеющую корни в точках v = kπ, то из нее можно вывести функции (sin u)’/sin u = ctg u и –(ctg u)’ = 1/sin²u, причем первая из полученных функций будет иметь v простым, а вторая — двойным полюсом. Построение требуемой эллиптической функции можно произвести аналогичным образом. Строится (в виде бесконечного произведения) целая функция  σ(u), имеющая корнями точки ω = m₁ω₁ + m₂ω₂ далее из нее логарифмическим дифференцированием выводится функция

и из этой функции выводится функция

Полученная функция φ(u) представляет собой искомую эллиптическую функцию 2 порядка: имеет числа ω₁ и ω₂ периодами и один двойной полюс в точке  ω = m₁ω₁ + m₂ω₂.

Представляется она в виде двойного ряда:

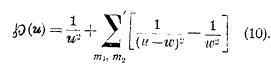
Если раньше построить эллиптическую функцию , то  из нее интегрированием можно вывести функции ζ и σ (этим путем и шел Вейерштрасс). Производная функции  есть также эллиптической функцией и между ними существует важное соотношение где инварианты g2 и g3 зависят от периодов. Это соотношение позволяет решить задачу об обращении эллиптической функции

, разрешая которую, мы приходим к эллиптическому интегралу в вейерштрассовой форме

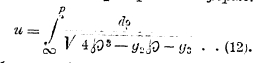
Наоборот, обращение интеграла (12), рассмотрение его верхнего предела, как функции величины интеграла, приведет нас к эллиптической функции Вейерштрасса . Три трансцендентые функции σ, ζ,  составляют основу вейерштрассовой теории эллиптических функций. Из них эллиптической является лишь функция ; две другие не периодичны, но при прибавлении к аргументу чисел ω₁ и ω₂ испытывают незначительные изменения (функция ζ приобретает постоянное слагаемое, а функция σ – постоянный множитель); кроме того, функция σ, как мы видели, целая, а ζ имеет 1 простой полюс. Функция  четная, а две другие нечетные. Любую эллиптическую функцию оказывается возможным выразить либо через функцию σ(u), либо через ζ и ее производные (формула Эрмита), либо через  и . Через функции Вейерштрасса выражается и интеграл от эллиптической функции, вообще не являющийся сам эллиптической функцией. Для вейерштрассовых функций существует также ряд формул сложения и приведения, как и для якобиевых; при этом эллиптическая функция  обладает алгебраической теоремой сложения, т. е.  (u₁+u₂) алгебраически выражается через (u₁) и  (u₂). Этим свойством обладает всякая эллиптическая функция (Вейерштрасс показал, что всякая однозначная трансцендентная аналитическая функция, обладающая теоремой сложения, будет либо рациональной функцией от показательной, либо эллиптической функцией).  Функции Якоби и Вейерштрасса просто между собой связаны. Так, между  и sn u существует соотношение:

где А и В постоянные, зависящие от инвариантов. Наряду с функцией α, во многих отношениях сходной с функцией θ Якоби, оказывается целесообразным ввести еще три функции σ_i (i=1, 2, 3), аналогичные функции тэта.

Теория эллиптических функций более стройно развертывается на основе функций Вейерштрасса, в приложениях же более значительная роль принадлежит эллиптическим функциям Якоби.

Введение эллиптических интегралов и функций, усилив аппарат интегрального исчисления, значительно обогатило средства математического анализа. С эллиптическими функциями и интегралами приходится иметь дело во многих вопросах прикладной и чистой математики. Так, эллиптические функции встречаются в механике при изучении движения маятника, простого и сферического; ими пользуются при интегрировании уравнений движения твердого тела, в некоторых вопросах теории упругости и теории потенциала. К эллиптическим интегралам и функциям приводят задачи нахождения длины дуги эллипса, гиперболы, лемнискаты, геодезических линий на поверхностях 4-го порядка и пр.; с помощью эллиптических функций разрешается проблема униформизации (параметрического представления) кривых 3-го порядка и вообще кривых I рода. В эллиптических функциях интегрируются дифференциальные уравнения Пикара, в частности уравнение Ламе; ими пользуются в некоторых вопросах алгебры (уравнения 5-й степени)  и теории чисел (вопрос о разложении числа на сумму квадратов). В теории конформного отображения с помощью эллиптических функций производится отображение многоугольных областей на верхнюю полуплоскость. Методами теории конформных преобразований можно также воспользоваться для изучения свойств эллиптических функций; с другой стороны, рассмотрение этих преобразований для некоторой группы отображений приводит к интересной категории функций с  естественной границей, не могущих быть аналитических продолженными на всю комплексную плоскость (см. XLV, ч. 2, 46), к открытым Клейном (1890) модулярным эллиптическим функциям.

Литература: A. M. Legendre, «Traité des fonctions elliptiques et des intégrales Eulériennes», 1825-28; С. G. J. Jacobi, «Fundamenta nova theoriae functionum ellipticarum», Königsherg, 1829; K. Weierstrass, «Mathematische Werke, V-VI — Elliptische Funktionen», 1915. С. Briot et J. С. Bouquet, «Theorie des fonctions elliptiques», 2 éd., Р., 1875; G. Н. Halphen, «Тгаіté des fonctions elliptiques», Р., 1886; Р. Appell et Е. Lacour, «Principes de la theorie des fonctions elliptiques», Р., 1897 (нов. изд. 1922); А. G. Greenhill, «The Applications of Elliptic Functions», L.— N-Y., 1892; А. Cayley, «Elliptic Functions», 1895; А. Enneper u. F. Müller, «Elliptische Funktionen», 1892; F. Klein u. R. Fricke, «Theorie der elliptischen Modulfunktionen», 2 В., Lpz., 1890, 1892;  R. Fricke, «Die elliptischen Funktionen», v. I—1916, v. II-1923; А. Hurwifz и. R. Courant, «Funktionen-theorie», 3 Aufl., 1929 (русский перевод в двух отдельных книгах: А. Гурвиц, «Теория аналитических и эллиптических функций», Л.-М., 1933, и Р. Курант, «Геометрическая теория функций комплексной переменной», Л.-М., 1934): А. Krazer, «Lehrbuch der Thetafunktionen», В., 1930; М. А. Тихомандрицкий, «Теория эллиптических интегралов и эллиптическая функция», Х., 1895; Д. Граве,   «Элементарная теория эллиптических функций», 1910. — См. также общие курсы: «Сours de М. Hermite», rédigé en 1882 par М. Andoyer  (4 éd., Р., 1891; русский перевод — Ш. Эрмит, «Курс анализа», М.-Л., 1933); Е. Goursat, «Cours d’ Analyse mathématique», t. II, 5 éd , Р., 1927 (русский перевод 1933); Е. F. Whittaker and G. N. Watson, «А course of modern analysis», Cambridge, 4-th ed., 1927 (русский перевод, ч. II, Л.-М., 1934); В. И. Смирнов, «Курс высшей математики», т. III, М.-Л., 1933. — Таблицы эллиптических функций и интегралов см., например, Jahnke u. Еmае, «Funktionentafeln», Lpz., 1923; по-русски — С. П. Глазенап, «Математические и астрономические таблицы», Лнг., 1932; Я. Н. Шпильрейн, «Таблицы специальных функций», ч. II, М.-Л., 1934.

А. Школьник.