Исчисление (Исчисление вариаций)

Исчисление вариаций.

Исчисление вариаций, или вариационное исчисление, есть учение об изменении величин, значение которых зависит от вида входящих в эти величины функций. Если мы имеем какое-нибудь выражение, например, z = х + у, где х — независимое переменное, а у — некоторая его функция, то изменение значения z может происходить от двух различных причин. Если вид функции у дан, например, у = х², то значение z зависит только от значения переменного х, например, при х = 2, z = 6, при х = 3, z = 12. Но если вид функции у может меняться, то значения z могут изменяться даже в том случае, когда значение переменного х остается без изменений. Так, если у = х² то, при x = 2, z = 6; если же у = х³, то, при том же значении х = 2, будем иметь z = 10. Исследование тех изменений в значениях выражений, содержащего неопределенные функции, которые зависят от изменении в значении независимого переменного, составляет предмет дифференциального исчисления (см. исчисление бесконечно малых). Исследование тех изменений, которые происходят от изменения вида функции, входящих в данное выражение, составляет предмет вариационного исчисления.

Главная задача вариационного исчисления состоит в взыскании maxima и minima — те и другие вместе называются также extrema — выражений, зависящих от неопределенных функций; обыкновенно такими выражениями являются определенные интегралы. Таким образом, в дифференциальном исчислении мы ищем те значения независимых переменных, при которых данное выражение обращается в maximum или minimum, а в вариационном исчислении мы ищем тот вид  функций, входящих в данное выражение, при котором это выражение обращается в maximum или minimum.

Различие между задачами дифференциального исчисления и вариационного исчисления можно видеть из следующих двух примеров. Пусть на плоскости дана точка М (2, 3) с координатами х = 2, у = 3 (см. Геометрия), и требуется найти на оси х точку, расстояние которой от данной точки М было бы наименьшим. Пусть будет х абсцисса искомой точки; так как точка лежит на оси х, то ее координата у равна пулю. Расстояние между двумя точками с координатами (х, у) и (x', у') выражается формулой √(х — х')² + (у — у')². В нашем случае у = 0, х' = 2, у'= 3, и потому искомое расстояние будет √(х—2)² +3². Это выражение представляет функцию от х, и в задаче требуется найти то значение х, при котором это выражение будет minimum. Поступая по правилам дифференциального исчисления, составляем производную, которая будет

(х—2 )/ √(х—2)² +3²

Эта производная обращается в нуль при х = 2. Следовательно, minimum будет при х = 2, и будет равен 3. Что это будет именно minimum, а не maximum, видно из того, что при всех значениях х, кроме х = 2, выражение под корнем имеет значение большее, нежели З². С другой стороны, рассмотрим такую задачу. На плоскости даны две точки М₀ (1, 2), в М₁ (3, 8), где числа в скобках представляют координаты обеих точек; требуется провести между обеими точками линию, длина которой была бы наименьшая, т. е. была бы меньше длин всех других линий, проходящих через те же точки. Пусть будет у = f(х) уравнение искомой линии; здесь f(х) — неизвестная функция, вид которой требуется определить. Так как искомая кривая должна проходить через точки (1, 2) и (3, 8), то функция должна принимать при х = 1 значение 2, а при х = 3 значение 8. Кроме того, так как длина линии у = f(х) между точками М (1, 2) и N (3, 8) выражается, как это доказывается в дифференциальной геометрии, интегралом

то функция f(х) должна быть такова, чтобы при постановке f(х) вместо у в предыдущий интеграл, последний приобретал значение меньшее, чем при всякой другой функции. Следовательно, в рассматриваемой задаче ищется вид функции, обращающей данный интеграл в minimum; и потому это задача из области вариационного исчисления. Ниже будет показало, что в данном случае функция f (х) должна иметь вид ах + b, где а и b постоянные, и следовательно, уравнение искомой линии будет у = ах , т. е. уравнение прямой. Таким образом, вариационное исчисление подтверждает известное положение, что прямая линия есть кратчайшее расстояние между двумя точками.

Обращаясь к изложению оснований метода вариационного исчисления, мы ограничимся рассмотрением задачи о maxima и minima простых (однократных) определенных интегралов, зависящих от одной неизвестной функции и ее первой производной. Общий вид такого интеграла

где F – данная  функция от х, у, у' и у' = dy/dx. Требуется найти вид функции у = f(х) под условием, чтобы при этом виде интеграл J имел наибольшее или наименьшее значение сравнительно с значением того же интеграла для всякого другого вида функции у. Прежде, чем дать общее решение этой задачи мы рассмотрим, в  виде примера, приведенную выше задачу. Пусть на плоскости даны две точки М₀ (х₀, у₀) и (х₁, у₁), и требуется провести между ними линию наименьшей длины. По предыдущему, для решения этой задачи, надо найти функцию f(х), которая, будучи поставлена на место у в интеграле

давала бы этому интегралу меньшее значение, нежели всякая другая функция, близкая к f(х). Возьмем вспомогательную функцию φ(х, λ), содержащую, кроме х, еще переменный параметр λ. Подчиним функцию φ(х, λ) следующем требованиям: функция φ(х, λ) должна обращаться при λ=0 в искомую функцию f(х), т. е. должно быть φ(х, 0) = f(х); далее, φ(х, λ) должна обращаться при х = х₀, и х = х₁ соответственно в у₀ и y₁ при всяком значении параметра λ. Геометрически это значит, что мы рассматриваем непрерывное семейство линий у = φ(х, λ), соответствующих различным значениям параметра λ; все эти линии проходят через точки М₀ (Х₀, у₀) и М₁ (х₁, у₁), и среди них, при λ = 0, находится искомая линия у = f(х) (черт. 1).

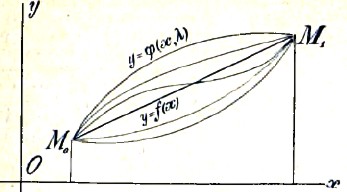
Черт.1

В последующем вам будет нужно брать производные по λ от различных функций, содержащих параметр λ, и давать в этих производных параметру λ значение λ = 0. Такие производные называются вариациями функции и обозначаются символом δ. Таким образом, если f(х) получается из

В последующем мы будем понимать под у искомую функцию f(х), так что будем обозначать δf(х) через δу. Так как вариация получается дифференцированием по параметру λ, то, на основании независимости производных от порядка дифференцирования (см. исчисление бесконечно малых), мы имеем, при некоторых ограничениях, которых мы здесь не будем касаться, что

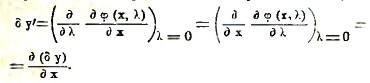
Внесем в интеграл J вместо у функцию φ(х, λ). Это значит, что мы рассматриваем этот интеграл не для искомой линии у = f(х), а для всех линий семейства у = φ(х, λ). Очевидно, что после такой подстановки интеграл J будет зависеть от параметра λ, и мы получим minimum пли maximum интеграла J при том значении λ, при котором обращается в нуль производная dJ/dλ (см. исчисление бесконечно малых). По предположению, этот minimum соответствует λ = 0; поэтому мы должны иметь

или, обозначая интеграл J при λ=0 черев J₀, δJ₀ = 0. Так как при λ=0 φ(х, λ) обращается в f(х), то, обозначая f(х) через у, будем иметь

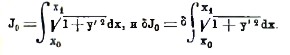
В интегральном исчислении доказывается, что если пределы интеграла постоянны, а подынтегральная функция содержит переменный параметр, то, чтобы дифференцировать определенный интеграл по параметру, нужно дифференцировать подынтегральную функцию. Поэтому, имеем

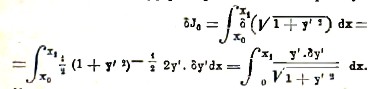
Интегрируем полученное выражение по частям (см. исчисление бесконечно малых), полагая

y’/√1+y’² = u, δy’. dx=dv; так как, по предыдущему δy’ = d(δy)/dx, то dv = d(δy)/dx dx = dδy, и v = δy. Поэтому, интегрируя по частям, находим

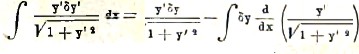
Отсюда, подставляя пределы интеграла, имеем

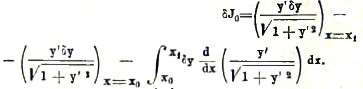
В этом выражении вариация δу представляет производную по параметру λ от φ(х, λ), взятую при λ = 0. По условию, функция φ(х, λ) обращается при х = х₀, х = х₁ соответственно в у₀ и в y₁ каково бы ни было значение λ; следовательно, при х = х₀ и х = х₁ φ(х, λ) не зависит от λ, а потому при этих двух значениях х производная ∂φ(х, λ)/∂λ, а следовательно, и

обращается в нуль. Поэтому в предыдущем выражении для J₀ члены, свободные от интеграла, обращаются в нуль, и мы имеем

Это выражение должно обращаться в нуль, так как в нем у представляет искомую функцию f(х), обращающую интеграл J в minimum. Легко видеть, что здесь вариация δу представляет совершенно произвольную функцию от х, подчиненную лишь условию, что она, как было показано выше, обращается в нуль при х = x₀ и х = x₁. В  самом деле, если мы хотим, чтобы δу обращалось в какую-нибудь функцию g(х), то стоит только взять φ(х, λ) = f(х) + λg(х). Докажем, что для того, чтобы δJ₀ обращалось в нуль, необходимо, чтобы было

d/dx (y’/√1+y’²) = 0

Положим, что d/dx (y’/√1+y’²) не обращается тождественно в нуль; тогда мы можем выбрать δу так, чтобы δJ₀ не был нулем. Для этого нужно только принять за δу такую функцию от х, которая для всех значений х имела бы знак одинаковый с знаком d/dx (y’/√1+y’²) и обращалась бы в нуль при х = х₀, х =х₁. При таком выборе δу подынтегральная функция δу.d/dx (y’/√1+y’²)  будет всюду положительна; а так как определенный интеграл есть предел суммы, у которой слагаемые суть значения подынтегральной функции, умноженные на соответствующие приращения независимого переменного (см. исчисление бесконечно малых), то, при таком выборе δу, интеграл, представляющий δJ₀  будет равен не нулю, как это должно быть, а положительному числу. Отсюда следует, что δJ₀ будет тождественно с нулем только в том случае, если у, или, что то же, f(х) будет удовлетворять условию

d/dx (y’/√1+y’²) = 0.

Это условие представляет дифференциальное уравнение второго порядка относительно у (см. исчисление бесконечно малых). Из него находим

y’/√1+y’² = с, где с – произвольное постоянное, или

y’ = c/√1-c², и затем

Обозначая здесь c/√1-c² через а, получим уравнение искомой линии в виде y=ax+b. Это уравнение представляет, как было сказано выше, прямую. Произвольные постоянные а и b определяются из того условия, что искомая линия должна проходить через точки М₀ и М₁; подставляя в уравнение прямой координаты обеих точек, получим два уравнения у₀=ах₀+b, у₁=ах₁+b, из которых и найдем а и b.

После этого примера, обратимся к решению общей задачи. Дан интеграл

J = ∫_x0^x1F(x, y, y’)dx, где F(x, y, y’) данная функция от x, y, y’; требуется найти функцию у=f(х), для которой интеграл имел бы наибольшее или наименьшее значение по сравнению с значением того же интеграла при других видах функций у, близких к f(х). При этом предполагаем, что пределы интеграла х₀ и х₁, суть данные числа, и что искомая функция f(х) должна иметь при х=х₀ и х=х₁ данные значения у=у₀, у=y₁. Геометрически это значит, как и в предыдущем примере, что мы ищем из числа кривых, проходящих через  точки М₀ и М₁, такую, для которой данный интеграл был бы maximum или minimum.

Поступая, как в предыдущем  случае, рассмотрим семейство кривых у =φ(x,λ), удовлетворяющих вышеуказанным условиям, и найдем производную интеграла J по параметру λ при λ=0, т. е. δJ₀, обозначая через J₀ то, во что обращается интеграл J, если у обращается в искомую функцию f(х). Поступая по предыдущему, находим

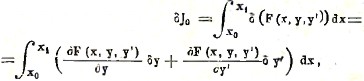
или, разбивая интеграл на два слагаемых

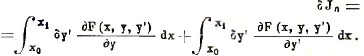
Интегрируем второй интеграл по частям, полагая

и находим

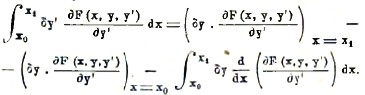
По условию φ(х, λ) обращается при х=х₀ и х=х₁ соответственно в y₀ и y₁ при всяком λ; следовательно, при этих значениях переменного х φ(х, λ) не зависит от λ, и потому производная dφ(х, λ)/dλ, обращается при этих значениях переменного х в нуль; то же относится и к

Поэтому в последнем выражении члены, свободные от интеграла, обращаются в нуль, и, соединяя вместе два остающихся интеграла, будем иметь

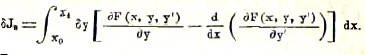
Рассуждая, как в предыдущем примере, убеждаемся, что для того, чтобы J₀ было maximum или minimum, функция у = f(х) должно обращать в нуль подынтегральный множитель

Приравнивая этот множитель нулю, получим для определения у дифференциальное уравнение второго порядка

Его общий интеграл даст искомую функцию у = f(х, а, b) с двумя произвольными постоянными (см. исчисление бесконечно малых), которыми можно воспользоваться для того, чтобы полученная кривая проходила через обе данные точки М₀ и М₁.

Приравнивая нулю вариацию определенного интеграла δJ₀ и интегрируя получающееся отсюда дифференциальное уравнение ∂F/∂y – d/dx (∂F/∂y’) = 0, мы находим функцию у = f(х), обращающую этот интеграл в maximum или minimum. Какой из этих двух случаев имеет место — этот вопрос решается рассмотрением второй вариации интеграла J₀, подобно тому, как в дифференциальном исчислении maximum и minimum функции различаются знаком второй производной. Вторая вариация δ²J₀ есть значение d²J/dλ² при λ = 0. Иcследование второй вариации позволяет дать необходимые условия для того, чтобы функция f(х) обращала интеграл J в maximum или minimum.

К числу задач, рассматриваемых в вариационном исчислении, принадлежат также задачи об условных extrema определенных интегралов, или изопериметрические задачи. В них ищется extremum определенного интеграла под условием, чтобы некоторый другой определенный интеграл имел заданное значение.

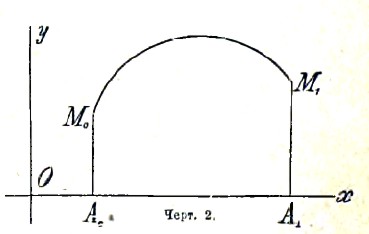
Чер.2

Найдем, например, кривую М₀М₁ (черт. 2), длина которой дана, под условием, чтобы площадь А₀М₀М₁А₁, ограниченная этой кривой, была больше площади, ограниченной каждой другой кривой, проходящей через те же две точки М₀(х₀, у₀) и M₁(x₁, у₁) и имеющею такую же длину. Площадь А₀М₀М₁А₁ выражается интегралом

∫_х0^х1f(x)dx или ∫^х1dx, если у = f(х) есть уравнение искомой кривой (см. исчисление бесконечно малых); длина кривой М₀М₁ выражается, по предыдущему, интегралом ∫_х0^х1√1+y’²dx.

Таким образом, задача сводится к нахождению максимума интеграла ∫_х0^х1y dx под условием, чтобы интеграл ∫_х0^х1√1+y’²dx имел данное значение.

Следуя методу, предложенному Эйлером, будем искать уже не условный, а абсолютный максимум суммы

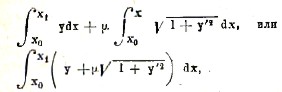
где μ – некоторый числовой множитель, который мы определим впоследствии. Применяя к этому новому интегралу выведенное выше правило для нахождения maximum или minimum определенного интеграла, мы имеем в данном случае

Поэтому, уравнение ∂F/∂y - d∂F/dx∂y² = 0 обращается в

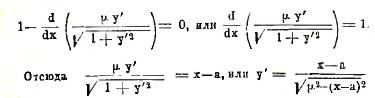
где а – произвольное постоянное. Вторичное интегрирование дает

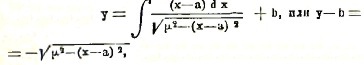
или, освобождаясь от радикала (x-a)²+(y-b)² = μ², где b – другое произвольное постоянное. Это уравнение представляет окружность с центром в точке (a, b) и радиусом μ (см. геометрия). Три постоянных, a, b, μ, входящие в уравнение окружности, определяются из условия, чтобы эта окружность проходила через обе данные точки М₀, М₁, и чтобы ее дуга М₀М₁ имела требуемую длину.

Общий метод для решения задач вариационного исчисления был дан впервые Эйлером. Дальнейшими значительными успехами в области вариационного исчисления мы обязаны Лагранжу, Лежандру, Якоби и др. В конце 70-х годов прошедшего столетия Вейерштрасс предложил особый метод для вывода условий maxima и minima определенных интегралов, в связи с более широким определением вариации; этот метод характеризует новое направление в вариационном исчислении.

Приложения вариационного исчисления весьма многочисленны. В геометрии одно из наиболее значительных   приложений вариационного исчисления представляет теория геодезических линий на поверхностях, т. е. линий, имеющих между двумя данными точками наименьшую длину; таковы, например, на поверхности шара окружности больших кругов; другое приложение вариационного исчисления — теория минимальных поверхностей, т. е. поверхностей, имеющих внутри данного контура площадь меньшую, чем все другие поверхности, проходящие через тот же контур. В механике вариационное исчисление применяется к отысканию линий и поверхностей, обладающих известными максимальными или минимальными свойствами. Так, при помощи вариационного исчисления можно найти форму тяжелой нити, укрепленной в двух точках. Но наиболее важным применением вариационного исчисления к механике представляется вывод основных уравнений механики из некоторых общих предположений, т. н. общих принципов, или начал, механики. Среди этих начал наиболее замечательны: начало Гамильтона и начало наименьшего действия.

Основы вариационного исчисления излагаются во многих руководствах высшего анализа, например, в книге Поссе, «Курс дифференциального и интегрального исчислений», в Курсах Jordan, Serret и др. Специально по вариационному исчислению можно указать на книги Вolza, «Vorlcsungen über Variationsreclmung»; Knеser, «Lehrbuch der Variationsrechnung»; Pascal, «Die Variationsrechnung», Hadamard, «Calcul des variations», также Сибинин, «Курс вариационного исчисления».

Б. Млодзеевский.