Кристаллография (Специальные отделы кристаллографии)

Специальные отделы кристаллографии.

Кристаллографические измерения представляют основу наблюдательной кристаллографии. Кристаллография могла вступить на научный путь лишь тогда, когда стал накопляться материал по измерению углов между гранями кристаллов и, следовательно, когда в распоряжении исследователей явились приборы для этого измерения, так называемые гониометры. Впервые такой прибор, хотя еще и примитивного устройства, был изобретен Каранжо, учеником Роме Делила, первым ученым, собравшим довольно значительный материал наблюдений, изложенный в его сочинении «Traité de cristallographie» (1783). Этот первый прикладной гониометр состоял из обыкновенного транспортира, известного из курсов элементарной геометрии, с присоединением двух рычажков, вращающихся около центра. Прикладывая эти рычажки к двум   граням кристалла перпендикулярно к ребру их пересечения, непосредственно на лимбе транспортира отсчитываем угол. Хотя прибор этот не потерял своего значения и до настоящего времени в случаях: 1) когда кристаллы очень велики, а 2) когда грани кристалла не блестящи (например, для моделей), он для громадного большинства кристаллов оказывается слишком грубым в сравнении с гониометрами, построенными на принципе отражения.

Рис. Гониометр

Ясно, что если, вращая около общего ребра двух граней и смотря по определенному направлению на грань кристалла, мы последовательно увидим отражение от правильно поставленного сигнала два раза (от обеих граней), то угол, на который повернем кристалл, будет точно равен углу между перпендикулярами к обеим граням.

Первый такой отражательный гониометр был построен Волластоном (Wollaston 1812), и он сейчас же вытеснил прикладные гониометры из бывшей практики наблюдений. Но для точности наблюдений с этим прибором требуется соблюдение многих условий, почему, все-таки, применение его связано с большой затратой времени и различными трудностями. Одну из этих трудностей — необходимость совмещать ось инструмента с ребром пересечения —  устранил Митчерлих, заменив внешний сигнал обыкновенным коллиматором, в фокусе которого вставляется диафрагма с прорезанным сигналом, за которым ставится источник света; тогда выходящие из коллиматора лучи почти строго параллельны, каковыми они остаются и после отражения от плоскости кристалла. Практически можно заменить коллиматор далеко поставленным сигналом; на расстоянии нескольких сажен возможная ошибка измерения становится уже ничтожной.

Громадное сокращение операций с одновременным приобретением многих преимуществ и устранением многих встречавшихся раньше погрешностей произошло при введении универсальных (или теодолитных) гониометров в 1889 г. Е. С. Федоровым и в 1892 г. В. Гольдшмидтом. Чтобы составить себе хотя некоторое представление о преимуществах этого метода, достаточно указать на то, что раньше нужно было переклеивать и юстировать кристалл для каждой пары граней, между которыми измерялся угол; под юстированием подразумевается весьма точная операция приведения ребра пересечения граней (хотя бы его на кристалле и не было) в положение, строго параллельное одной из осей вращения инструмента, и в результате измерения получался только один угол. Теперь кристалл юстируется только один раз для полного измерения кристалла, и в результате каждой установки грани получается отсчет двух углов поворота около двух взаимно-перпендикулярных осей. Изображение такого гониометра, вполне удовлетворяющего всем обычным целям измерения, находится на приложенной фигуре. На нем прямо видны два лимба: один горизонтальный — для измерения углов поворота около неподвижной вертикальной оси, и вертикальный — для измерения углов поворота около подвижной (а именно вращающейся около неподвижной вертикальной) горизонтальной оси; в этой вращающейся части для уравновешения с противоположной стороны помещается груз, служащий и удобной ручкой для этих поворотов. Там, где обе оси, вертикальная и горизонтальная, пересекаются, т. е. в центре прибора, остающемся неподвижным при всех вращениях, наклеивается маленький кристалл (и, в общем, чем меньше кристаллик, тем точнее измерение); на этот же центр направляется и ось трубы, видной слева; ясно, что при правильном помещении кристаллика он будет виден в эту трубу в увеличенном виде (если опустить подвижную лупу в объективе, которая изображена приподнятой). Сам кристаллик наклеивается на пластинке, прикрепленной к юстирному прибору, а на этом приборе несколько винтов, которые позволяют всячески передвигать и поворачивать кристаллик и тем дают возможность привести его в правильное положение. Сигнал (например, в виде лампы с линзой, в главном фокусе которой находится пламя) ставится в отдалении, и приблизительно параллельные лучи от него, падая на кристалл, только при исключительных положениях граней, отражаются точно по направлению оси трубы. И для того, чтобы от такого положения одной грани перейти к точно такому же положению другой грани, нужно, вообще, произвести два вращения; как около неподвижной, так и около подвижной оси. Вот этим-то двум углам поворота, отсчитываемым по обоим лимбам, и присваивается название сферических координат, вполне и однозначно определяющих положение каждой данной грани. По этим-то двум координатам получается на стереографической сетке определенная точка, как гномостереографическая проекция грани (см. кристаллографические проекции). Получив же в проекции изображение всех граней кристалла, мы легко решим все относящиеся сюда задачи, возникающие при его описании или для других целей (например, для целей определения вещества по методу кристаллохимического анализа нужно найти числа символа комплекса).

Как упомянуто выше и как теперь становится ясным из описания прибора, он становится неприменимым в случае очень больших и тяжелых кристаллов, которые, конечно, уже не могут удержаться в висячем положении на воске. Но такие кристаллы и встречаются весьма редко, и применение их для целей кристаллоизмерения не может рекомендоваться, так как это измерение, во всяком случае, приведет к сравнительно грубым результатам: ведь трудно искусственно получить крупные кристаллы; чем они меньше, тем легче их получить и тем чаще они встречаются. Но так как такие кристаллы,  все-таки, встречаются, и встречается также надобность их измерить, то можно применить упомянутый выше прикладной гониометр Каранжо. Имея ввиду, что от применения этого прибора теряются все преимущества, которые отчасти отмечены выше для универсального метода, были построены универсальные прикладные гониометры (и также впервые В. Гольдшмидтом в 1896 г. и Федоровым в 1909 г.). Здесь, конечно, не место перечислять и объяснять все преимущества употребления универсальных гониометров. Но нельзя не упомянуть, что именно то обстоятельство, что здесь в результате измерения каждой грани получаются две ее сферические координаты, во много раз сокращает утомительную работу последующих вычислений. Если же, вообще, точных вычислений не требуется, а достаточно графической точности, как например, в обыкновенных случаях производства кристаллохимического анализа, то не только само измерение, но и решения нужных графических задач приводят к затрате минимального времени: в среднем около двух часов, а в исключительных случаях даже часа, а иногда и получаса. Тем знаменательнее, что такое говорящее само за себя обстоятельство большинством работающих кристаллографов (чаще всего и минералогов) долгое время игнорировалось, хотя постепенно одни лица за другими и переходили к  новой системе. Впрочем, к настоящему времени к применению этого метода перешло едва ли не большинство (для такого маленького шага понадобилась четверть столетия).

Кристаллохимический анализ имеет целью определять вещества, полученные в форме кристаллов. Эта задача могла носиться в уме первого представителя научной кристаллографии Гаюи, до конца жизни пребывавшего в убеждении, что каждому чистому веществу свойственна своя, и притом только одна, форма. Уже в конце его жизни прямой опыт показал, что веществу одного и того же химического состава может принадлежать и не одна, а большее число форм, а Митчерлиху пришлось наблюдать, что и разным, хотя химически и весьма родственным, веществам может быть свойственна одна и та же или, по крайней мере, весьма близкие формы. Первое свойство названо полиморфизмом, второе — изоморфизмом.

Эти свойства вещества лишь несколько усложняют применение этого анализа, хотя в некоторых отношениях и облегчают его. Иногда число изоморфных веществ достигает нескольких десятков; в силу близости форм все эти десятки можно рассматривать за одну, хотя и несколько растяжимую, форму, а это в значительной степени сокращает работу по составлению таблиц и разрежает самые таблицы. Но, с другой стороны, это обстоятельство вызывает потребность различать отдельные вещества одной группы, а это почти всегда достигается простыми химическими пробами. Таким образом, в этом анализе, действительно, совмещаются две работы весьма различного характера: работа кристаллографического описания, основанная на измерении кристаллов и употреблении гониометра, с другой — чисто химическая работа пробы, почти всегда весьма простой. Ради большей достоверности определения можно воспользоваться и другими, легко определяемыми, характерными для вещества свойствами, как то: его окраской, его твердостью, способностью колоться, оптическими свойствами и пр.

Долгое время после Гаюи главное основание для этого анализа — кристаллографическое описание формы — казалось безнадежным в силу того, что постоянными в форме кристаллов данного вещества являлись углы между гранями составляющих его форм, но формы вообще слагаются в комбинации, а комбинации кристаллов одного и того же вещества, полученного в разных условиях, весьма различны. Но ближайшее подробное изучение вопроса привело к выводу, что, хотя комбинации и весьма переменны, но все-таки между ними есть формы, появляющиеся с довольно упорным постоянством и представляющие важнейшие из его форм, тогда как остальные приходится считать второстепенными или даже случайными. В некотором числе случаев являются условия, препятствующие образованию даже этих относительно постоянных   форм, но, выражаясь статистически, такое аномальное появление форм скорее составляет исключительное явление, и в таком случае, понятно, метод кристаллохимического анализа может не дать желательного результата — определения вещества. Поэтому возник вопрос опытного порядка — определить, в каком относительном числе случаев, благодаря этой, а отчасти и благодаря другим причинам (например, ошибкам, допущенным при составлении таблиц, а их по существу очень трудно избежать по неполноте данных), применение метода этого анализа не приводит к цели. Этот опыт был произведен над материалом в количестве около ста веществ (присланных под условными Ж№изразных центров Европы) в Горном институте в 1910—» акад. году и привел к заключепию, что из четырех веществ определяется пе меньше трех.

Опубликование полученных результатов в статье «Praxis in der kristallochemischen Analyse» (в «Zeitschrift für Kristallographie», L 513)   вызвал повсюду живое внимание и оценку особых преимуществ этого, в сущности, единственного общего метода, если не считать простейших неорганических соединений. Одни авторы подчеркивали то ничтожное количество вещества, которое нужно для таких определений. Так, например, Орелкин определил присутствие кристаллического белкового вещества — вителлина в составе телейтоспор ржавчины (Puccinia graminis Persoon), имея в распоряжении всего 0,05 гр. Другие отмечали, что при этом методе определяемое вещество не подвергается разрушению, а сохраняется. Но, конечно, главными преимуществами метода является затрата очень малого количества времени, если не считать самой кристаллизации, и точное индивидуализирование материала: как бы ни был сложен химический состав вещества, определение по этому методу нисколько не усложняется и всегда состоит из ряда простых и постоянно одних и тех же операций, к которым только в случае изоморфных веществ приходится неизбежно присоединять химическую пробу; если вещество проявляется в нескольких разновидностях, то обыкновенно эти разновидности резче всего отличаются именно по кристаллическим формам.

Здесь не место излагать ту научную теорию¹⁾, которая легла в основание применения этого метода, тем более, что это в более или менее общедоступной форме изложено в сборнике № 5 «Новые идеи в химии», выходящем под редакцией профессора Л. А. Чучаева (1914). Но из литературы, отозвавшейся на первое опубликование этого метода, в которой, между прочим, появились указания и на то, что для применения этого метода подготовительные работы появились и в западноевропейской ученой литературе, нельзя не привести отзыва известного английского кристаллографа Ф. Баркера (занимавшегося у автора этого метода в Горном институте и не только знакомившегося, но вместе с другими лицам и принявшего участие в составлении таблиц для этого анализа): «почему геометрический метод отожествления веществ (кристаллохимический анализ) не был раньше разработан кристаллографами и передан в распоряжение химиков? Ответ на это дается теми большими трудностями в классификации материала — составление таблиц для определения, — коих до Федорова никому не удавалось преодолеть, чтобы воспользоваться этими свойствами для определения; мало того, является вопросом, делал ли кто-нибудь до него даже попытки в этом направлении» («Crystallochemical analysis» в «The chemical News», CVI № 2761, р. 199).

¹⁾  Основания этой теории были изложены в «Allgemeinste Kristallisationsgesetze und die darauf fussende eindeutige Aufstellung der Kristalle» в «Zeits. Für Kristallogr.» 38, 321 (1904).

 

III. Кристаллографические проекции служат не только и даже не столько для изображения наблюдавшихся форм кристаллов, сколько для решения задач, к ним относящихся, как то: определения по изображению величин углов между гранями, определения их символов, точно выражающих их относительное положение, и т. п. Конечно, графическое решение задач вообще не отличается большой точностью, но обыкновенно удовлетворительно решает поставленный вопрос. Для целей кристаллохимического анализа, измерив на гониометре определяемый кристалл, в результате чего непосредственно получается определенная (гномостереографическая) проекция, необходимо получить несколько определенных чисел», составляющих так называемый символ комплекса, и тогда именно эти числа на специально составленных таблицах и определяют испытуемое вещество. И на это обычно требуется несколько минут времени.

Если через кристаллик пропустить катодный луч (Рентгена), то вызываемые им в кристаллике волны обусловливает дифракцию, а последняя отпечатывает на фотографической пластинке большую группу точек, которая, являясь следствием структуры кристалла, составляет натуральную проекцию его комплекса. От одной же данной проекции определенными построениями можно перейти ко всем остальным. Но так как эта натуральная проекция сравнительно сложна, то, чтобы понять ее, нужно сначала выяснить простейшие. Таковыми, прежде всего, являются линейные и стереографические.

Первые получаются, если, приняв некоторый постоянный центр Z, будем проводить из него лучи, параллельные возможным ребрам кристалла: каждый из них на плоскости чертежа (принятой, например, на расстоянии одного дециметра от центра) отметит точку, которая и есть линейная проекция этого ребра. Если через тот же центр Z проведем плоскость, параллельную грани кристалла, то эта грань отметит на плоскости чертежа прямую, которая и есть линейная проекция грани. Но можем изобразить грань и точкой, если из того же центра к ней восставим перпендикуляр; его линейная проекция есть точка, но так как сам перпендикуляр относится к плоскости, то эта точка служит точным выражением положения грани и обычно называется гномонической проекцией грани; это то же, что линейная проекция перпендикуляра.¹⁾

¹⁾ Впервые эту проекцию применил Нейманн («Beitrage zür Kristallonomie», 1823).

 

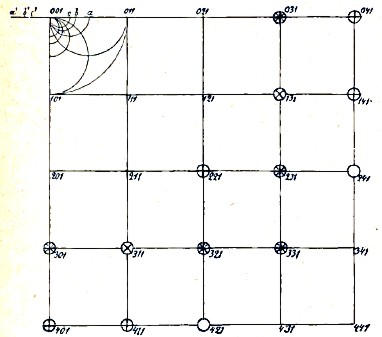
На приложенной фигуре вершины квадратов изображают в гномонической проекции те грани, которым принадлежат поставленные при этих точках символы.

Стереографические проекции были известны еще во времена Птолемея (но считают вероятным, что они исходят от Гиппарха, «отца астрономии»). Эти проекции обычно употребляются в географии (например, при изображении земных полушарий) и их легко связать с проекциями линейными. Если мы основание перпендикуляра из центра Z на плоскости чертежа примем за центр О шара, имеющего своим радиусом отрезок ZO, и будем проводить из него прямые, параллельные ребрам кристалла, или перпендикуляры к граням, то получим точки на поверхности шара, а прямые, соединяющие эти точки с центром Z, отметят на плоскости чертежа точки, которые и представляют граммастереографические проекции; и в этом случае граммастереографическая проекция перпендикуляра называется гномостереографической проекцией соответственной плоскости. Перпендикуляр к плоскости чертежа дает на ней точку О, которая есть одновременно линейная и граммастереографическая проекция этого перпендикуляра и, в то же время,  есть гномоническая и гномостереографическая проекция плоскостей, параллельных плоскости чертежа. Вообще же, гномоническая проекция а некоторой грани и гномостереографическая проекция той же грани а' суть точки различные; прямая а делает с перпендикуляром ZO вдвое больший угол, чем прямая Za’; но именно это простое соотношение показывает, как легко перейти от гномонической проекции к гномостереографической; оно же составляет и переход от линейной проекции к граммастереографической.

Если мы поместим обыкновенный круговой конус таким образом, чтобы его центр (иногда неправильно называют «вершина») был в точке Z и чтобы его поверхность проходила чрез перпендикуляр ZO, то получится его линейная проекция в виде эллипса, проходящего чрез центр О (этот эллипс и есть разрез конуса плоскостью чертежа). Но если мы переместим его центр в точку О, двигая по тому же перпендикуляру, то он не только пересечет поверхность шара в круге, но и его граммастереографическая проекция также будет кругом, проходящим чрез точку О; от точек эллипса, как линейных проекций, мы перешли к граммастереографическим проекциям и в результате вместо эллипса получили круг.

Если возьмем на плоскости какой-нибудь круг с центром О и радиусом r, то найдем, что каждая точка А на плоскости находится на каком-нибудь радиусе этого круга; и мы всегда эту точку можем заменить на том же радиусе другою точкой А’ так, чтобы произведение отрезков ОАхОА' равнялось постоянной величине r². Чем дальше от центра возьмем точку А, тем ближе к центру получим точку А', а если представим себе точку А бесконечно удаленной, то точка А’ совместится с центром О. Такая операция называется преобразованием обратными радиусами (или реципрочным). Всякий круг на плоскости, как известная совокупность точек, преобразуется в другой круг (и оба будут иметь общие касательные, проведенные из центра О). Прямая же при этом преобразуется в круг, непременно проходящий чрез центр О, так как па всякой прямой имеется бесконечно удаленная точка. И вот, если примем круг, проведенный на фигуре, и имеющий центром точку (001) за круг реципрочного преобразования, то все стороны квадратов преобразуются в круги, проходящие чрез этот центр, как это и сделано на фигуре. Точки пересечения прямых, то есть вершины квадратов, преобразуются в точки пересечения кругов, и, конечно, обе преобразуемые друг в друга точки будут находиться на одном радиусе. В результате мы получаем новую проекцию, полученную из гномонической; в последней точки располагаются на прямых, в первой — на кругах. По этой причине новая проекция называет гномоциклической. На деле все круги и их точки пересечения нужно заменить диаметрально противоположными по отношению к центру (001). В частности, вместо точек а, b, с получаются точки а', b', с'. В новой геометрии круг, служащий для такого преобразования, называется мнимым кругом реципрочного преобразования. Его центр — точка (001), а радиус — сторона квадрата.

Но на полученные круги мы можем смотреть как на граммастереографические проекции конусов; если от них перейдем, как объяснено выше, к линейным проекциям тех же конусов, то круги преобразуются в эллипсы, также проходящие чрез тот же общий центр, и проекция станет гномоэллиптической. Точки пересечения эллипсов выразят определенные грани, символы которых мы прямо можем прочесть на нашей фигуре. Вот такая-то группа точек и получается на фотографических пластинках при пропускании рентгеновского луча чрез кристаллик. Отсюда видим, что эта натуральная проекция, или рентгенограмма, есть гномоэллиптическая проекция граней комплекса фотографируемого кристалла. Только фотографируемые точки не удовлетворяют геометрическому понятию о точках (таковые не были бы и видны), а скорее представляют небольшие, и не всегда достаточно отчетливые пятна. Этим, так сказать, установлена азбука, позволяющая нам читать книгу о строении кристаллов, даваемую нам природой при употреблении рентгеновских лучей.

На фигуре, вместо пятен, непосредственно получаемых на фотографической пластинке, отмечены особыми знаками точки разных символов. Эти знаки условно показывают, что наиболее яркие пятна принадлежат граням (031), (231), (331), дальше по яркости принадлежат граням (131), а самые слабые пятна принадлежат граням (241). Такая рентгенограмма получена Б. Л. Браггом для кристаллов хлористого калия¹⁾.

¹⁾   W. L. Bragg. “The structure of some crystals as indicated by their diffraction of Xrays” (‘Proceedings of the Royal Soc.”, 1913, 89 248).

 

Как видим из изложенного, не только для разных целей целесообразнее употреблять те или другие проекции, но что иногда определенные проекции навязываются нам самой природой, и нам остается только раскрыть их значение. В этом отношении полезно упомянуть о той проекции, в которой нагляднее всего изображается правильное расположение точек, как это имеет место в кристаллах и как это мало-помалу раскрывается более детальным изучением кристаллов. В этой проекции для изображения мы пользуемся векториальными кругами. Это те же круги, но с отмеченной на их окружности стрелкой, которая может быть направлена вправо или влево. Если изображаемая точка не находится на плоскости чертежа, то, значит, она отстоит от него на некотором расстоянии r; и вот мы проектируем эту точку перпендикулярно к плоскости чертежа, а основание этого перпендикуляра принимаем за центр векториального круга, имеющего радиусом величину r; если точка лежит ниже плоскости чертежа, мы отмечаем круг, как правый векториальный круг; если она находится выше, то отмечаем его как левый. Ясно, что при этом условии положение точки, изображенной таким векториальным кругом, становится вполне отчетливо; оно отчетливо даже тогда, когда обе точки находятся на одном перпендикуляре и на равном расстоянии от плоскости; в этом   случае на круге отмечены и стрелка вправо, и стрелка влево. Иногда полезно для большей наглядности изображения уменьшать в определенное число раз величины радиусов, изображающих кругов. В этом всегда можно условиться, и такое условие нисколько не вредит точности изображения, равно как и решению возникающих при этом задач.

Кристаллографические вычисления стали потребностью науки с того времени, как был выведен закон Гаюи (см. кристаллография). Потребность эта усилилась и усложнилась, когда Вейсс ввел понятие о кристаллографических осях и кристаллы стали определяться такими осями с принадлежащими им единичными отрезками. Формулы для этих вычислений были сначала заимствованы из общих отделов математики, а особенно из сферической тригонометрии, которая к этому времени давала их в достаточной полноте; но так как при этом особенно часто имеют дело с целыми числами, связанными линейными соотношениями, то весьма естественно, что с развитием учения об определителях (детерминантах) пришлось прибегнуть и к изящным выражениям этого учения. Например, выражение закона поясов Вейсса получило такую форму: две данные грани, кристаллографические символы которых есть (р1 р2 р3) и (q1 q2 q3), пересекаются в ребре (оси пояса), символ которого выражается числами

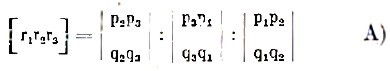
Формулами аналитической геометрии стремился воспользоваться сначала К. Науманн («Lеhrbuch der Kristallographie», 1829); ими же, с присоединением построений и формул новой геометрии, пользовались Миллер и, еще более систематически, Либиш («Physikalische Kristallographie», 1879) и, наконец, Е. С. Федоров («Этюды по аналитической кристаллографии», 1886—88). Но в последнем (четвертом) из этих этюдов автор вводит уже новую систему проективных вычислений, специально приспособленную для целей кристаллографии, связывая ее в то же время с пользованием универсальным гониометром (см. кристаллографические измерения), отчего дело вычислений значительно упрощается.

Чтобы понять эту систему, нужно принять во внимание, что в ней вычисления производятся по особенно простой формуле, непосредственно применимой лишь для кристаллов кубической сингонии, а именно:

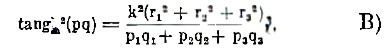
где р и q означают грани с указанными выше символами, а r1, r2, r3 — символы ребра их пересечения по формуле А).

Для кристаллов других сингоний нужно эти числа заменить другими (уже иррациональными) числам р’, q’, получаемыми по формулам:

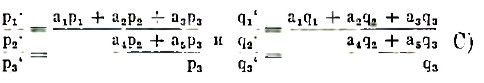
для самого сложного случая кристаллов триклинной сингонии, а уже для кристаллов моноклинной сингонии формулы эти еще более упрощаются и принимают вид:

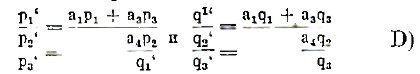
и наконец для кристаллов ромбической сингонии принимают вид:

Но в самое последнее время тем же автором выведены формулы, по которым вычисления сводятся к простым сложениям и вычитаниям. Это крайнее упрощение вычислений связано с той особенностью кристаллографического комплекса, по которой он выводится из четырех его данных граней. Вывод этих формул приведен в «Основных формулах сферической и плоской тетрагонометрии» («Записки Горного института», IV, 373). Вкратце они приведены в сборнике № 5 «Новые идеи в химии» (см. тетрагонометрия).

Е. Федоров.