Теоретические основания математики

Теоретические основания математики.

1. Общая задача теоретического обоснования математики. Теоретические  основания математики в настоящее время превратились в самостоятельную дисциплину, служащую фундаментом всего современного точного знания. Вряд ли в области математики есть отрасль, потребовавшая столь напряженной работы мысли, как обоснование ее начал. Возникновение учения об основах математики и его эволюция имели троякий источник: методологический, гносеологический и фактический. Методологический путь заключался в постоянном стремлении провести построение всех отделов математики строго логически — дедуктивно; гносеологический путь наметился в процессе разыскания источников математического познания; наконец, фактический источник исследований, относящихся к теоретическим основаниям математики, обусловливался тем, что фактическая разработка математического материала при достаточном его углублении сделалась невозможной без строгого обоснования начал математики. Не может подлежать сомнению, что именно этот последний путь к развитию учения о теоретическом основании математики в действительности привел ко всем остальным вопросам, сюда относящимся. Элементарные эмпирические сведения из геометрии и арифметики, которыми располагали вавилоняне и египтяне, пестрили ошибками. Первые шаги в деле более углубленного развития математики эти ошибки раскрыли. Нужно было не только их исправить, нужно было найти гарантии к тому, чтобы их избежать в будущем.  Средства для этого заключались в том, чтобы в основу всей математики положить  небольшое число истин, которые не вызывали бы никакого сомнения, и из них вывести весь материал этой науки. Эпоха перехода от эмпирической математики к такому логическому ее построению, в деталях этого процесса, теряется в глубокой древности. Памятники античной науки развертывают уже глубоко продуманную в указанном смысле систему.

Методологический подход к обоснованию математики начинает эту работу мысли. Логическая обработка математики определенно сложилась и дала плодотворные результаты только в Греции. А так как в Греции преобладала геометрия, оставившая далеко позади все остальные отрасли математики, то дедуктивное направление сказалось, прежде всего, в греческой геометрии. Задача заключалась в том, чтобы построить систему геометрии в форме непрерывной цепи логических выводов, разматывающихся из небольшого числа основных положений — определений и аксиом. Определениями устанавливается смысл основных понятий, которыми геометрия оперирует; аксиомы устанавливают их основные свойства. Все остальное должно составить строго логический вывод из этих исходных положений.

Такие попытки дать строго логическое обоснование геометрии относятся к глубокой древности. Еще в V столетии до н. э. геометр Лев уже составил такого рода трактат по геометрии; за ним последовали другие работы того же рода. Но ни одно из этих сочинений до нас не дошло; все они были забыты, когда появилось одно из величайших произведений научной мысли — «Начала» Евклида (см. XIII, 323/27).

2. Система геометрии у Евклида. В тринадцати книгах «Начал», посвященных преимущественно геометрии, Евклид не только дает строго продуманную систему геометрии, но также глубоко проникает в учение о числе. Собственно геометрии посвящены книги І-VІ и ХІ-ХІІІ; они содержат весь тот материал, который ныне принято называть элементарной геометрией. Все построение выполнено для того времени с таким совершенством, что вполне оригинальным творением одного человека оно быть не могло; оно несомненно представляет собой результат преемственного творчества нескольких поколений эллинских геометров, которое получило свое завершение в бессмертном труде Евклида. Каждая книга начинается рядом определений, постулатов и аксиом. Под постулатами (αίτήματα — требования) Евклид разумеет чисто геометрические положения — элементарные свойства геометрических образов, настолько очевидные, что их без всяких сомнений и колебаний можно принять за исходные положения. Самое же наименование «постулаты», т. е. требования, обусловливается диалектическим методом преподавания и распространения научных идей, который господствовал в Греции в Александрийскую эпоху. Это делалось путем беседы-диспута; постулаты — это были те положения, которые должен был принять диспутант, чтобы он был уже по необходимости вынужден признать все дальнейшее, что желал установить руководитель диспута; это были логические требования, которые руководитель диалога или диспута предъявлял к остальным его участникам. В частности, таким образом, постулаты геометрии — это те требования, которые руководитель предъявляет к лицу, приступающему под его руководством к изучению геометрии: он должен признать их для себя ясными, неоспоримыми, он должен эти требования принять, и тогда он будет вынужден признать все последующее. И это гарантирует и его и науку от ошибок.

Кроме постулатов, у Евклида есть еще аксиомы,  κοιναί έννοιαι, т. е. общие достояния нашего ума. Это — положения, которые не представляют собой специфически геометрических истин; это — положения более общего свойства, находящие себе применение не только в геометрии, но и вне ее. У Евклида аксиомы носят все же математический характер, но не чисто геометрический. Например — две величины, порознь равные третьей, равны между собой. Это положение будет справедливо независимо от того, будут ли это величины геометрические (длины, площади, объемы), арифметические (числа), или механические (скорости, силы) и т. д.

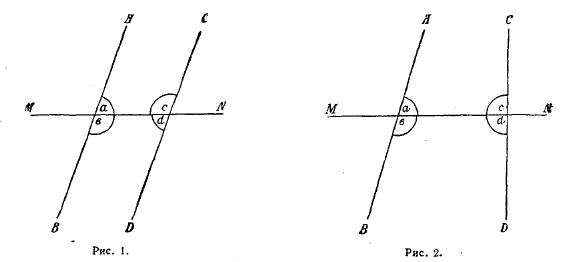
Рис. 1. 2.

Сочинения Евклида дошли до нас в различных списках и изданиях, не вполне тождественных между собой. В область определений, постулатов и аксиом падают наибольшие расхождения, вследствие которых было трудно точно установить различие между аксиомами и постулатами; сомнения в этом отношении остаются и по настоящее время. Первой книге Евклида в издании эллинистов Гейберга и Менге («Euklidis opera omnia», ediderunt et latine interpretati sunt J. Heiberg et Н. Menge, 1883—1916, 8 тт.), которое признается лучшим, предпосланы следующие пять постулатов: требуется — 1) чтобы от каждой точки к каждой другой точке можно было провести прямую линию, 2) и чтобы каждую ограниченную линию можно было продолжать неопределенно, 3) и чтобы из любого центра можно было описать окружность любым радиусом, 4) и чтобы все прямые углы были равны и 5) чтобы всякий раз, как прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.

Первые четыре из этих постулатов совершенно ясны, пятый же выражен тяжело; так как он играет чрезвычайно важную,  можно сказать, доминирующую роль в развитии учения об основаниях геометрии, то, необходимо его совершенно отчетливо разъяснить. На каждом из рис. 1 и 2 изображены две прямые АВ и CD, расположенные в одной плоскости и пересеченные третьей прямой MN. С каждой стороны секущей MN образуется два внутренних односторонних угла: а, с и b, d. Но на рис. 1 углы эти в каждой паре дополняют друг друга до 2 d, так что а + с = 2d и b + d = 2d, на рис. 2 сумма углов а и с меньше 2d, а сумма углов b и d больше 2d: а + с < 2d, b + d > 2d. В первом случае прямые АВ и CD не пересекутся, сколько бы мы их ни продолжали; Евклид это без труда доказывает. Во втором случае прямые АВ и CD должны при достаточном продолжении пересечься со стороны углов а и с, т. е. с той стороны, с которой сумма внутренних односторонних углов меньше 2d. Доказать это Евклид не в состоянии и потому ставит это положение как исходное требование, как постулат.

Эти постулаты в связи с определениями  и аксиомами составляют, таким образом, те теоретические основания, которые Евклид делает базой своей геометрической системы. Все остальное должно составить логический вывод из этих положений. Как уже сказано, система в этом отношении глубоко продумана. Особенно характерным для евклидовой разработки геометрии  является чистота геометрического метода в том смысле, что Евклид не прибегает ни к каким средствам, чуждым чистой геометрии; он не пользуется даже арифметическими средствами, которые — к слову сказать — в ту пору были очень слабы. Это направление позже выразили словами geometriam geometrice (геометрию геометрически). Даже учение об отношениях и пропорциях проведено Евклидом (по-видимому, по схеме, ранее установленной Евдоксом) без малейшего уклона в сторону арифметики; это учение есть одно из замечательнейших творений греческого гения.

Достоинства «Начал» Евклида, именно как выдержанной логической системы, настолько высоки, что в течение почти двух тысячелетий с ними не могло конкурировать ни одно сочинение по геометрии. Все руководства по геометрии представляли собой те же «Начала» Евклида, несколько более приспособленные для понимания учащихся, но по существу мало от них отличавшиеся. При всем том, уже в глубокой древности философы, уделившие «Началам» много внимания, пришли к сознанию, что, при всех высоких достоинствах «Начал» Евклида, его творение, как строго логическая дедуктивная система, все же чрезвычайно далеко от совершенства. Всякое дедуктивное логическое построение по существу своему должно быть формальным. Из посылок «все А суть В» и «все В суть С» вытекает «все А суть С». Это строго логический вывод (силлогизм Barbara). Правильность вывода здесь совершенно не зависит от того, что мы разумеем под терминами А, В и С. Не от содержания понятий, которыми мы оперируем в дедуктивном построении, не от тех образов и представлений, которые мы с этими понятиями соединяем, зависит правильность дедукции, а от формы, по которой посылки и сделанный из них вывод построены: если эта форма соблюдена, то умозаключение правильно, какое бы содержание мы ни вкладывали в термины, входящие в посылки. Это именно разумеют, когда говорят, что чисто дедуктивный вывод по существу своему неизбежно носит совершенно формальный характер; и в этом его коренное отличие от диалектической логики.

Применяя эти соображения к геометрической дедукции, мы приходим к тому, что строго логический вывод геометрического предложения также должен носить совершенно формальный характер, т. е. должен основываться исключительно на правилах построения силлогизма, а не на тех образах, которые мы соединяем с геометрическими понятиями. Мы определенным образом представляем себе прямую линию, плоскость, круг, многоугольник. Если эти представления играют роль в ходе умозаключения, то чистой дедукции уже нет: вывод представляет собою смесь логического умозаключения и наглядных, интуитивных соображений. Между тем, если разрешить себе свободно пользоваться интуицией, то тяжелый аппарат Евклида во многих своих частях будет не нужен; сомнительно даже, есть ли надобность доказывать многие геометрические предложения, которых интуитивная ясность не вызывает никаких возражений. В этом порядке развертывается геометрическое творчество, идущее всегда путем интуитивного усмотрения и его примирения с возникающими от неправильной интуиции противоречиями; на этой точке зрения мы стоим и в настоящее время, когда обучаем начаткам геометрии детей. Но не на этой точке зрения стоял Евклид. Он ставил себе совершенно определенно задачу развить геометрию из небольшого числа предпосылок — определений, постулатов и аксиом — строго логически, — следовательно, дедуктивно, формально. Но выполнить эту задачу в полной мере ему далеко не удалось. Его дедукция, часто поражающая необычайной тонкостью мысли, все же грешит против требований формальной логики почти в каждом его рассуждении, в каждом доказательстве. Вот через внутреннюю точку круга проведена прямая; Евклид утверждает, что эта прямая пересечет периферию круга. На чем основано это утверждение? На том, что это ясно глазу, на тех наглядных представлениях, которые мы соединяем с прямой и с кругом. Две крайние точки отрезка лежат на двух различных сторонах треугольника; Евклид утверждает, что все остальные точки отрезка лежат внутри треугольника. Ясно, что он апеллирует здесь к интуиции. Легко понять, что Евклид совершенно бессилен это утверждение доказать, потому что среди его определений нет определения понятий «внутри» и «вне», нет, следовательно, материала, на котором можно было бы такое доказательство основать. Число таких отступлений от чистой дедукции у Евклида чрезвычайно велико; дедукция и интуиция постоянно переплетаются в его системе. При всей своей стройности, при всей своей мощи, логически она еще далека от действительного установления теоретических основ геометрии.

Между тем действительное и безупречное установление этих основ — то под напором развертывавшегося фактического материала, то в обстановке общего направления философской мысли — в высшей мере занимало умы геометров и философов, начиная с современников Евклида и до наших дней. И так как в пору, весьма близкую к Евклиду, уже выработалось сознание, что система Евклида не удовлетворяет всем требованиям формальной логики, то очень рано возникают попытки восполнить эти пробелы. Этой задачей занимаются многочисленные авторы, известные под общим названием комментаторов Евклида.

3. Комментаторы Евклида. Из античных комментаторов наиболее замечательные – Папп  и Прокл, из средневековых — Клавий, а позднее Саккери; из арабских комментаторов — Анариций и Нассер-Эддин, из более поздних — англичанин Грегора и французский геометр Лежандр (см.). Каждый из этих комментаторов утверждал, что совершенно освободил творение Евклида от всяких упреков. Саккери отметил это даже в самом названии своего сочинения — «Euklides аb omni naevo vindicates» (Евклид, освобожденный от всякого пятна). И все же эти широковещательные обещания и наименования совершенно не соответствовали действительному содержанию сочинений. Комментаторы заменяли одни аксиомы другими, видоизменяли определения, углубляли то или иное доказательство, но по существу неизменно впадали в те же ошибки, которые делал Евклид; они опирались на интуицию, на образные представления, доверяя глазу там, где нужен был строго формальный логический вывод. Каждый комментатор обстоятельно критиковал не только Евклида, но и своих предшественников; это было не так трудно. Но действительно продвинуть выполнение задачи о строго логическом обосновании геометрии вперед, хотя бы в некоторой степени, очень мало кому удавалось. Теоретические основания геометрии даже после Лежандра оставались еще столь же недостаточно выясненными, как и в эпоху Евклида.

Впрочем, одна заслуга остается за комментаторами Евклида совершенно несомненная: они отчетливо выяснили слабые стороны «Начал», осветили все их дефекты. По существу, дефекты эти сводятся к следующему. 1) Самое слабое место в системе Евклида составляют определения: они в большинстве случаев содержат весьма мало тех признаков, на которых могла бы быть основана формальная дедукция. Основные определения Евклида представляют собой краткие описания тех образов, которые мы связываем с основными понятиями. Эти определения можно было бы в этом смысле назвать интуитивными, а не формальными. Насколько мало эти определения полезны для чисто дедуктивной системы, можно судить по тому, что Евклид нередко на протяжении всей книги не пользуется тем или другим определением, приведенным в начале ее. 2) Основные положения Евклида недостаточны для формального обоснования геометрии. Почти в каждом доказательстве он неявно принимает еще и другие постулаты и аксиомы, им не формулированные и явно не высказанные. 3) Почти в каждом рассуждении Евклида  дедукция переплетается с интуицией, и правильность заключения подтверждается не только логикой, но и глазом. В особенности в тех случаях, когда Евклиду приходится говорить о внутренних или внешних точках той или иной фигуры, он руководствуется, исключительно интуицией.

Комментаторы Евклида заменяли его определения другими, часто более неудачными; они увеличивали число постулата и аксиом; они заменяли одни постулаты другими; и все-таки существенного улучшения не получалось; дедукция все же оставалась несовершенной, логика все же оставляла широкий простор интуиции. И иначе оно быть не могло, пока геометр оставался на той позиции, которую занимали все «составители начал»: от предшественников Евклида до последователей Лежандра — они все исходили из определенных пространственных образов, их геометрия была наукой об этих образах. И потому их геометрия, неразрывно связанная с представлениями об этих образах не могла освободиться от интуиции, не могла претвориться в чисто формальную логическую систему. Чтобы этого достигнуть геометр должен был совершенно порвать с какими бы то ни было наглядными представлениями. Прошло много времени, пока геометры решились стать на эту точку зрения; путь к ней лежал через неевклидову геометрию.

4. Пятый постулат Евклида. Неевклидова геометрия, это замечательное творение абстрактной мысли, явилась после исследований, связанных с пятым постулатом Евклида. Содержание этого постулата выяснено выше. Всякий, кто сравнит его с остальными постулатами, обратит внимание на то, что содержание его не столь просто, не столь элементарно, как содержание остальных постулатов Евклида. На это не приходится даже обращать внимание изучающего предмет, это само бросается в глаза. В самой системе Евклида постулат занимает своеобразное место. Первые 28 предложений «Начал» не зависят от пятого постулата в том смысле, что при их доказательстве к этому постулату прибегать не приходится. Эти 28 предложений содержат свойства смежных и вертикальных углов, свойства прямого угла, условия равенства треугольников, теорему о внешнем угле треугольника (он больше каждого из внутренних, с ним не смежных), соотношения между углами и сторонами в одном и том же треугольнике, соотношения  между длиной перпендикуляра и наклонных, идущих из одной и той же точки к прямой. Предложение ХХVІІІ устанавливает (рис. 3), что сумма внутренних односторонних углов а и в, которые пересекающиеся прямые АВ и CD образуют с секущей MN с той ее стороны, с которой происходит пересечение, меньше 2d. По существу содержание этого предложения сводится к тому, что сумма двух углов треугольника MNP меньше 2d (а + b < 2d). Это предложение далее нужно обратить. Обращение гласило бы: если две прямые (конечно, на плоскости) при пересечении их третьей образуют с ней внутренние односторонние углы, сумма которых не равна 2d (т. е. с одной стороны секущей меньше 2d, а с другой ее стороны больше 2d), то эти прямые с той стороны, с которой сумма меньше 2d, при достаточном продолжении неизбежно пересекутся. Справедливость этого предложения ясна всякому, кто естественно связывает с основными геометрическими понятиями обычные пространственные представления. Отсюда возникло естественное стремление доказать это (обращенное) предложение. По-видимому, не один геометр до Евклида напряженно старался найти доказательство этого предложения. Но эти старания ни к чему не привели; доказать его не удалось, и Евклиду ничего не оставалось сделать, как включить это предложение в число основных положений, принимаемых без доказательства, т. е. в число постулатов. Это положение и составляет содержание пятого постулата. Когда оно принято, то геометрия разматывается далее уже без особых затруднений, — конечно, в пределах тех требований, которые мы к системе Евклида можем предъявить. Впрочем, в дальнейшем встречается еще много предложений, как в планиметрии, так в особенности в стереометрии, которые от пятого постулата не зависят, т. е. могут быть доказаны без его помощи. Но большинство дальнейших предложений геометрии существенно зависит от пятого постулата в том смысле, что их доказательство либо непосредственно опирается на этот постулат, либо опирается на предложение, доказанное при помощи этого постулата. Постулат, таким образом, как бы раскалывает геометрию на две части, из которых одна от постулата не зависит, тогда как в другой каждое предложение прямо или косвенно опирается на пятый постулат. Первую часть геометрии не совсем удачно называют абсолютной (иногда общей, «allgemeine Geometrie»), а вторую — евклидовой.

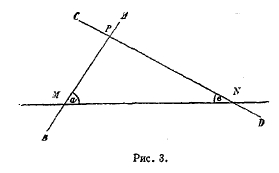
Рис. 3.

Эта своеобразная роль постулата, его внезапное появление уже глубоко в планиметрии, его сравнительная сложность, его значение, расчленяющее геометрию на две части, — все это казалось неправильным, ненормальным, и уже в глубокой древности появилось стремление это исправить: для этого нужно было устранить постулат, как основное положение; нужно было доказать выражаемое им предложение при помощи остальных постулатов Евклида. Если бы это было выполнено, в теории параллельных линий не было бы неприятного пробела, геометрия не расщеплялась бы на две части, в ней царили бы полная гармония и единство. Это обстоятельство вызвало много усилий доказать постулат. Вследствие кажущейся элементарности этой задачи, не требующей больших знаний (ибо доказать предложение нужно, располагая только первыми 28 предложениями «Начал»), к ней обращались многие, владевшие лишь незначительной математической подготовкой. Но рядом с такого рода полуграмотными математиками задачей о восполнении пробела в теории параллельных линий занимались и весьма выдающиеся геометры. Более того, на протяжении двух тысячелетий, от Евклида до Лежандра, Гаусса и Гильберта, трудно указать выдающегося геометра, который не уделил бы внимания, а иногда и упорного труда этой как будто скромной элементарной проблеме. Неоднократно математическому миру возвещалось, что эта трудность уже преодолена, и позорное пятно в теории параллельных линий, порочащее всю геометрию, наконец, смыто. Но спокойное и тщательное обсуждение каждого предложенного доказательства неизменно обнаруживало в нем ошибку. Одни авторы возводили для доказательства постулата сложное построение, в котором, в конце концов, запутывались. Другие прибегали для доказательства этого элементарного предложения к учению о бесконечно малых, методы которого в пору формировавшегося еще анализа не были достаточно разработаны и часто приводили к грубым ошибкам. Но чаще всего слабая сторона доказательства заключалась в том, что автор незаметно для себя допускал вместо доказываемого предложения другое, по существу ему эквивалентное. Это новое допущение часто бывало значительно проще постулата в евклидовой его форме, — иногда даже несравненно проще; но дело от этого не менялось: задача заключалась не в том, чтобы заменить евклидов постулат более простым допущением, а в том, чтобы его доказать, не вводя нового допущения. Ламберт указывает, что доказательство евклидова постулата можно довести до такого положения, что остается, по-видимому, только совершенно незначительная мелочь. Но по тщательном размышлении оказывается, что в этой мелочи именно и заключается вся суть дела.

Постулат Евклида, прежде всего, служит краеугольным камнем теории параллельных линий. Точнее, дело обстоит следующим образом. Учение о параллельных линиях начинается рядом предложений, устанавливающих достаточные условия параллельности двух прямых. Если две прямые на плоскости при пересечении их третьей образуют с ней равные соответственные углы, или равные внешние накрест лежащие либо внутренние накрест лежащие углы, или если сумма внутренних односторонних либо внешних односторонних углов равна 2d, то прямые параллельны. Эти предложения очень просто доказываются без нового постулата. Но обращение их неизбежно требует постулата в той или иной его форме. Достаточно непосредственно принять любое из обратных предложений, и оно заменит евклидов постулат. Достаточно принять, что в плоскости через точку, лежащую вне прямой, проходит только одна прямая, не встречающая первой, — и это допущение заменит евклидов постулат. Можно придать постулату и различные другие формулировки. Существо дела заключается, конечно, не в том, как постулат выражен. Важно то, что все попытки обойтись вовсе без нового постулата в теории параллельных линий не увенчались успехом. Особенно замечательна связь между постулатом Евклида и вопросом о сумме углов треугольника. В евклидовой геометрии, как известно, сумма внутренних углов в треугольнике равна 2d. Точнее, это значит, что, если мы примем постулат Евклида, то легко докажем, что сумма внутренних углов каждого треугольника равна 2d. Что можно установить относительно суммы внутренних углов треугольника, не пользуясь постулатом Евклида? Относящиеся сюда простые, но чрезвычайно изящные исследования связывают обыкновенно с именем Лежандра; в действительности эти результаты были гораздо раньше получены Саккери (ХVII ст.) и Ламбертом (XVIII ст.). Сущность дела сводится к следующему. А priori относительно суммы углов в треугольнике можно сделать три предположения: она может быть больше 2d, она может быть равна 2d, она может быть меньше 2d. Но первое предположение отпадает: не пользуясь пятым постулатом, можно при помощи очень элементарных соображений доказать, что сумма внутренних углов треугольника не превышает 2d. Выбор остается только между двумя другими допущениями, а его без пятого постулата сделать невозможно. Правда, можно показать, что, если сумма углов хотя бы в одном треугольнике равна 2d, то она и во всяком другом треугольнике равна 2d; если же хотя бы в одном треугольнике сумма углов меньше 2d, то она и во всяком другом треугольнике меньше 2d. Но решить, которое из двух соотношений имеет место, нельзя, не опираясь на евклидов постулат. Если принять пятый постулат, то сумма углов равна 2d; если решиться допустить, что постулат несправедлив, нужно принять, что сумма углов треугольника меньше 2d. В этом последнем случае, как оказывается, сумма углов может меняться от треугольника к треугольнику, причем угловой дефект, т. е. недостаток суммы углов до 2d, должен быть пропорционален площади треугольника.

Такая же тесная связь существует между пятым постулатом и учением о подобии. Обычное построение теории подобия целиком основано на евклидовом постулате. Уже Валлис (1616—1703) показал, что достаточно допустить существование подобных фигур произвольного размера, чтобы получить всю геометрию Евклида. Учение о подобии, таким образом, существенно зависит от постулата. С учением о подобии неразрывно связана евклидова метрика: учение об измерении площадей и объемов; таким образом, и эта часть геометрии тесно связана с пятым постулатом.

Изложенное достаточно выясняет, как глубоко проникает пятый постулат в существо евклидовой геометрии.

5. Открытие неевклидовой геометрии. Многие пытались доказать пятый постулат от противного. Всякое доказательство от противного заключается в том, что доказываемое предложение предполагается ложным, т. е. отвергается, и из этого предположения делаются логические выводы. Можно сказать так: к предыдущим, уже установленным геометрическим аксиомам и теоремам присоединяется предложение, противоположное тому, которое требуется доказать, и из этого материала делаются логические выводы до тех пор, пока они не приводят к прямому противоречию с одним из установленных уже предложений. Такое противоречие устанавливает неправильность сделанного предположения и тем доказывает справедливость того предложения, доказать которое собственно имелось ввиду. Так именно и поступали все те, которые пытались доказать пятый постулат от противного. Делалось предположение, что пятый постулат несправедлив, и к абсолютной геометрии, уже установленной без помощи этого постулата, присоединялось предложение, ему противоположное. Из этого геометрического материала делались логические выводы в убеждении, что они приведут к  прямому логическому противоречию с ранее принятым. Став на этот путь, одни довольно быстро сбивались, усматривая противоречие там, где его в действительности не было. Нужно дать себе ясный отчет в том, что противоречие должно быть не интуитивное, а логическое; иными словами, цель нельзя считать достигнутой, когда мы придем к выводам, противоречащим нашим геометрическим представлениям: это ведь всегда бывает, как только  мы становимся на путь доказательства от противного. Чтобы действительно достигнуть цели, мы должны, как уже сказано, придти к противоречию логическому, т. е. мы должны придти к предложению, отрицающему то, что было принято нами ранее. Этого именно не понимали достаточно ясно многие из тех, которые становились на путь доказательства от противного; придя к выводу, ярко противоречащему нашим геометрическим представлениям, нашим пространственным образам, они считали вопрос исчерпанным. Другие их в этом изобличали, но сами делали то же самое, только продвинувшись по этому скользкому пути несколько далее. Но более глубокие мыслители умели пройти в этом направлении далеко.

Вступая на путь доказательства пятого постулата от противного нужно, как сказано, начать с того, чтобы принять, как предположение, противоположное допущение. Так как самый постулат, как мы видели, может получить весьма различное выражение, то весьма различны также и формы противоположного положения, из которого исходили доказывавшие постулат от противного.

Джироламо Саккери (Saccheri), итальянский монах, иезуит (1667—1733), исходит из вопроса о сумме углов треугольника (у него,  впрочем, несколько иначе поставленного). Здесь возможны, как мы уже видели, три гипотезы. С первой из них Саккери легко  справляется, доказывая, что сумма углов треугольника не может превысить 2d.  Остаются два предположения — евклидово, что сумма углов треугольника равна 2d, и противоположное, т. е. неевклидово, что эта сумма меньше 2d. Саккери принимает это последнее допущение, не придавая ему иного значения, как только предположения, которое должно привести к абсурду. Тонко разматывая выводы из сделанного допущения, Саккери устанавливает 32 предложения, к которым оно приводит; в 33-ем предложении он уже пользуется бесконечно большими и приходит к противоречию с абсолютной геометрией, которое он так настойчиво искал. В действительности, однако, это противоречие есть только плод недоразумения, вернее — плод неосторожного обращения с бесконечно удаленными точками, которое в эту эпоху было очень обычным. Сомнения в правильности этого заключения явственно проглядывают в дальнейших рассуждениях самого Саккери.

Философ и математик Ламберт, в середине XVIII ст., не знал работы Саккери, но шел по тому же пути, чуть-чуть иначе формулируя исходное положение. Развивая следствия, из него проистекающие, он также очень тонким рассуждением приходит к ряду предложений, которые имели бы место, если бы считать постулат Евклида ложным. Ламберт уже не впадает ни в какую ошибку: он ясно сознает, что ни к какому противоречию его допущение не приводит. Поражаясь, напротив, чарующей стройности, к которой его рассуждения приводят, он бессилен сделать отсюда окончательный вывод и только восторженно восклицает: «В этом есть нечто восхитительное, что вызывает даже желание, чтобы третья гипотеза была справедлива. И все же я желал бы, несмотря на это преимущество, чтобы это было не так, потому что это было бы сопряжено с рядом других неудобств. Тригонометрические таблицы стали бы бесконечно пространными, подобия и пропорциональности фигур не существовало бы вовсе; ни одна фигура не могла бы быть представлена иначе, как в абсолютной своей величине; и астрономии пришлось бы плохо».

По тому же пути безуспешных попыток доказать постулат Евклида от противного, сопровождаемых открытием замечательной цепи выводов, к которым приводит отрицание этого постулата, шли позже также другие талантливые математики, как, например, Вахтер, Тауринус, Швейкарт. Они углубили этот материал стройных выводов из парадоксального допущения и проложили путь геометру, который решился бы смелее занять позицию действительного отрицания евклидова постулата.

По-видимому, первый решительно и твердо стал на этот путь великий германский математик Гаусс (см.). Однако, за всю свою жизнь Гаусс ни разу не опубликовал своих взглядов на этот предмет, напротив того, он тщательно их скрывал, справедливо опасаясь той нетерпимости, которая будет проявлена математиками по отношению к этим чрезвычайно своеобразным идеям. Только из его переписки с друзьями и учениками (В. Больай, Ольберсом, Герлингом, Шумахером), опубликованной после его смерти, а также из оставленных им заметок, ныне опубликованных в VIII томе полного собрания его сочинений, видно, как глубоко Гаусс владел неевклидовой геометрией.

Впервые эти замечательные идеи были опубликованы в 1826 г. великим русским геометром, профессором казанского университета Н. И. Лобачевским (см.), а несколькими годами позже, совершенно независимо от Лобачевского, — чрезвычайно талантливым молодым венгерским математиком Иоанном Больай (см. Больэ). Основная мысль этик геометров заключалась в том, что, присоединяя к абсолютной геометрии постулат, противоположный постулату Евклида, как это делали все, пытавшиеся доказать постулат от противного, невозможно придти к противоречию, ибо его в этой комбинации посылок вовсе нет. Иными словами, с точки зрения логической нет ничего несообразного в том, чтобы отвергнуть пятый постулат Евклида и вместо него принять противоположное положение. Это положение также будет логически совместимо с остальными постулатами Евклида и приведет к стройной геометрической системе, глубоко отличающейся от евклидовой, но столь же совершенной и формально правильной. Эта неевклидова геометрия находится в резком противоречии с нашими интуитивными представлениями о геометрических образах; но логическая концепция все же остается совершенно безукоризненной. Это разительное противоречие между интуицией и логикой, разгадка которого была обнаружена лишь много позже, служило для многих выдающихся математиков непреодолимым препятствием для принятия неевклидовой геометрии. И лишь исключительная проницательность двух-трех гениальных мыслителей призвала к жизни и осветила этот новый мир замечательных геометрических идей.

6. Содержание геометрии Лобачевского-Больай. Лобачевский и Больай разными путями пришли к одной и той же своеобразной геометрической системе. Совершенно ясное представление об этой замечательной системе можно получить только путем терпеливого и основательного ее изучения. Здесь же о ней возможно дать только самое общее представление.

Рис. 4.

Пятый постулат Евклида Лобачевский берет в так называемой Плейфордовской форме, в которой он получает следующее выражение: в плоскости через точку О, лежащую вне прямой АВ (которая, конечно, лежит в той же плоскости), можно провести только одну прямую, не встречающую АВ. Противоположное допущение, следовательно, заключается в том, что через точку О, лежащую вне прямой АВ, в плоскости ОАВ, проходит больше одной прямой, не встречающей АВ. Это и есть исходное допущение Лобачевского.

Все прямые, проходящие в той же плоскости через точку О (рис. 4), распадаются относительно прямой АВ на две категории: первую категорию образуют прямые Q''Q', N''N', Р''Р', встречающие прямую АВ; вторую образуют прямые К''К', L''L', М''М', которые прямой АВ не встречают. Обе категории прямых отделяются одна от другой двумя прямыми А''А' и В''В'. Картина представляется в таком виде, что прямые, проходящие внутри вертикальных углов А''ОВ'' и В'ОА', пересекают прямую АВ, прямые же, проходящие внутри углов А’ОВ'' и А''ОВ’ ее не пересекают. Правильнее, следовательно, будет сказать, что прямые, проходящие через точку О, делятся относительно прямой АВ не на две, а на три категории: 1) пересекающие АВ, 2) расходящиеся с нею (т. е. проходящие внутри углов А’ОВ'' и А''ОВ’) и 3) прямые А''А’ и В''В', отделяющие прямые, расходящиеся с прямой  АВ, от прямых, ее пересекающих. Две прямые последней категории прямой АВ также не пересекают, но по обе стороны перпендикуляра ОР' это суть первые прямые, не пересекающие АВ. Эти две прямые Лобачевский называет параллельными прямой АВ в точке О. Термин этот имеет, таким образом, у Лобачевского не то значение, что у Евклида. Через каждую точку плоскости О проходят, следовательно, две прямые, параллельные данной прямой АВ. Но если рассматривать не прямые, а лучи, разумея под лучом АВ прямую АВ, направленную от А к В, а под лучом ВА — ту же прямую, направленную от В к А, то можно считать луч А''А' параллельным лучу ВА, а луч В''В' параллельным лучу АВ. При таком соглашении можно сказать, что в плоскости через каждую  точку О, лежащую вне луча АВ, проходит один и только один луч, параллельный лучу АВ. В этой форме предложение очень близко подходит к евклидову постулату; но, на самом деле, положение совершенно иное, потому что самое понятие о параллельности здесь существенно другое.

Лобачевский доказывает, что луч, параллельный другому лучу в одной из своих точек, параллелен ему и в каждой другой своей точке, т. е. в каждой из своих точек с надлежащей стороны производит отделение пересекающих прямых от не пересекающих.

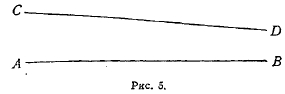
Рис. 5.

Он доказывает также, что два луча всегда взаимно параллельны, т. е. что, если луч СО II АВ, то и АВ II CD; благодаря этому мы можем говорить просто о двух параллельных лучах (не оговаривая, который из них параллелен другому). Далее, как и в евклидовой геометрии, два луча, параллельные третьему, параллельны между собой.

Рис. 6.

В таком виде представляется учение о параллельных линиях в геометрии Лобачевского. На нем непосредственно основывается учение о взаимном расположении прямых на плоскости. Если прямая CD пересекается с прямой АВ, то она, как и в евклидовой геометрии, беспредельно от нее отдаляется по обе стороны от точки пересечения. Если луч CD параллелен лучу АВ (рис. 5), то со стороны параллельности он неограниченно (асимптотически) приближается к АВ, никогда его не достигая; с другой же стороны неограниченно от него удаляется. Наконец, если луч CD расходится с АВ (рис. 6), то с той стороны, с которой он образует с перпендикуляром MN острый угол NMD, он сначала приближается к АВ, достигает наименьшего расстояния PQ и затем начинает с другой стороны перпендикуляра PQ симметрично относительно него удаляться от АВ; прямая же PQ перпендикулярна к обеим прямым. В евклидовой геометрии две прямые могут оставаться на одном и том же расстоянии одна от другой: этим свойством обладают две параллельные прямые. В плоскости Лобачевского это никогда не имеет места. Две прямые либо неограниченно расходятся одна от другой по обе стороны от общей точки (пересекающиеся прямые), либо неограниченно сближаются с одной стороны и неограниченно удаляются одна от другой с другой стороны (параллельные прямые), либо неограниченно удаляются по обе стороны от общего перпендикуляра (расходящиеся прямые). Аналогично дело обстоит с двумя плоскостями. Они могут пересекаться, — тогда они неограниченно удаляются одна от другой по обе стороны от линии пересечения; они могут быть параллельны, — тогда они неограниченно приближаются одна к другой вдоль пучка параллельных лучей; они могут расходиться, — тогда они имеют общий перпендикуляр, от которого неограниченно расходятся во все стороны. Все эти соотношения Лобачевский вполне строго доказывает, исходя из основных положений, которые легли в основу его системы, т. е. абсолютной геометрии и постулата, противоположного евклидову.

В дальнейшем развитии его системы основную роль играет одна геометрическая идея, чуждая новых допущений, но очень своеобразная по своему замыслу. Она связана с особого рода кривыми и поверхностями, существующими в неевклидовом пространстве, с т. н. предельными линиями и предельными поверхностями. Совокупность лучей, проходящих в плоскости через одну точку, образует пучок; общая точка называется центром пучка. Окружности, имеющие общий центр в центре пучка, представляют собой т. н. ортогональные траектории пучка, т. е. кривые, пересекающие все лучи пучка ортогонально, под прямым углом. Это имеет место, как в евклидовой, так и в неевклидовой геометрии. Совокупность параллельных лучей, как в евклидовой, так и неевклидовой плоскости, также рассматривается как пучок; это как бы пучок, центр которого лежит в бесконечности. Ортогональными траекториями такого пучка в евклидовой плоскости служат прямые, перпендикулярные к лучам этого пучка. Руководясь этими соображениями, в евклидовой геометрии часто говорят, что прямую можно рассматривать как окружность, центр которой лежит в бесконечности, или как окружность бесконечно большого радиуса. В неевклидовой плоскости ортогональными траекториями пучка параллелей служат не прямые, а замечательные кривые (рис. 7),  которые Лобачевский называет предельными кругами, или предельными линиями, или орициклами. Окружностями бесконечного радиуса здесь служат не прямые, как в евклидовой геометрии, а предельные линии. Замечательное свойство  предельной линии заключается в том, что она может скользить по самой себе, как прямая или окружность: она имеет одинаковую кривизну во всех своих точках. Вместе с тем, подобно прямым линиям, все предельные линии конгруэнтны между собой.

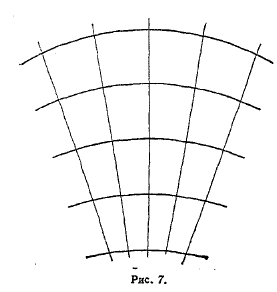
Рис. 7.

В пространстве совокупность лучей, проходящих через одну и ту же точку, образует  связку. Сферические поверхности, имеющие центр в центре связки, пересекают ортогонально все лучи связки. Если центр связки  «уходит в бесконечность», т. е., если связка состоит из параллельных лучей, то поверхностями, ортогонально эти лучи секущими, в евклидовом пространстве являются плоскости; в неевклидовом пространстве эту роль играют кривые поверхности, которые Лобачевский называет предельными поверхностями, или орисферами (рис. 8); лучи пучка называются осями орисферы. Орисфера обладает тем же свойством, что сфера и плоскость: она может свободно передвигаться по самой себе. Через каждую точку орисферы проходит ось. Если возьмем две точки О и А на орисфере (рис. 9) и через них проведем оси поверхности ОО' и АА', то плоскость, через эти две параллели проходящая, рассечет поверхность по предельной линии ОА. Таким  образом, на предельной поверхности через каждые две точки проходит одна и только одна предельная линия, как на плоскости через каждые две точки проходит одна и только одна прямая. Сечение предельной  поверхности всякой другой плоскостью, не проходящей через ось, есть окружность. В частности, если в какой-либо точке оси (К или К', лежащей с вогнутой стороны предельной поверхности, проведем к этой оси перпендикулярную плоскость, то она пересечет поверхность по окружности. Таким образом, предельная поверхность может быть рассматриваема как поверхность вращения вокруг любой из ее осей. Так как меридианами при этом служат предельные линии, то можно сказать, что предельная поверхность может быть получена вращением предельной линии вокруг любой из ее осей, совершенно аналогично тому, как сфера получается вращением окружности большого круга вокруг любого диаметра шара. Разница лишь в том, что орисфера есть поверхность разомкнутая, и ее диаметры как бы сходятся в бесконечности.

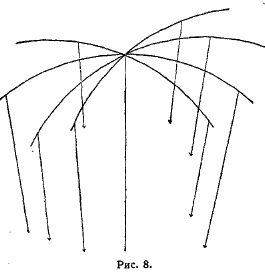
Рис. 8.

Геометрию плоскости, планиметрию, можно строить, не выходя из самой плоскости, основываясь на возможности свободного передвижения плоскости в самой себе; это свободное передвижение заключается в том, что каждую точку плоскости можно привести в совмещение с любой другой точкой, а затем вращением плоскости вокруг этой точки повернуть ее на любой угол. Основными образами, которыми оперирует планиметрия, являются прямые линии, прямолинейные углы и прямолинейные фигуры; изучение кривых линий, даже окружности, уже основывается на предварительном изучении прямой.

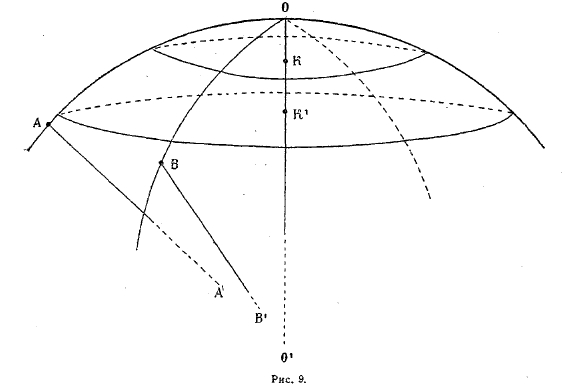
Рис. 9.

Аналогично этому строится геометрия сферы. И сфера может свободно передвигаться по самой себе, причем каждая точка может быть приведена в любую другую точку, и вращением вокруг любой точки сферу можно повернуть на любой угол. В геометрии сферы роль прямых в качестве  основного линейного образа играют окружности больших кругов. Геометрия сферы изучает эти окружности, углы треугольника и многоугольника, ими образуемые. Но так как окружности больших кругов на  сфере всегда пересекаются в двух точках, а не в одной, как две прямые, то геометрия сферы значительно отличается от геометрии плоскости.

Так как в неевклидовом пространстве предельная поверхность может гак же свободно передвигаться по самой себе, как плоскость или сфера, то Лобачевский занялся изучением геометрии предельной поверхности. За основной образ, соответствующий прямой на плоскости, Лобачевский здесь принял предельную линию. Она имеет  с прямой аналогию, заключающуюся в том,  что она определяется на предельной поверхности двумя точками и может быть неограниченно продолжена в обе стороны. Разматывая шаг за шагом геометрию на предельной поверхности, Лобачевский к  своему изумлению убедился, что эта геометрия — евклидова. Через каждую точку предельной поверхности можно провести  одну и только одну предельную линию, не  встречающую другой предельной линии;  сумма углов в треугольнике, составленном  из предельных линий, равна 2d и т. д.

Итак, двумерная евклидова геометрия не уничтожается тем, что мы отвергаем пятый постулат на плоскости: она возрождается на предельной поверхности. Это имеет и то значение, что вместе с ней возрождается и тригонометрия Евклида. Владея же тригонометрией на предельной поверхности, Лобачевский переходит от нее к тригонометрии на неевклидовой плоскости подобно тому, как мы в обыкновенной геометрии переходим от плоской тригонометрии к сферической. Чтобы дать некоторое представление о тригонометрии на неевклидовой плоскости, необходимо ознакомиться еще с одной весьма существенной идеей.

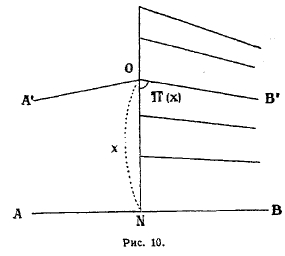
Рис. 10.

Из точки О, лежащей в некоторой плоскости (рис. 10), опустим перпендикуляр ON на прямую АВ, лежащую в той же плоскости. С точки зрения неевклидовой геометрии на плоскости через точку О проходят две прямые ОА' и OB', параллельные прямой АВ; луч ОА' параллелен лучу ВА, луч OB' параллелен лучу АВ. Оба луча образуют с перпендикуляром равные острые углы А'ON и В'ON. Эти углы, которые параллели образуют с перпендикуляром, Лобачевский называет углами параллельности. Величина угла параллельности зависит только от длины перпендикуляра ON: как Лобачевский легко доказывает, он убывает, когда длина перпендикуляра увеличивается, и возрастает, когда длина перпендикуляра уменьшается. При неограниченном возрастании расстояния ON (т. е. при неограниченном удалении точки О от прямой АВ по перпендикуляру NО) угол параллельности неограниченно уменьшается: параллель все приближается к перпендикуляру, образуя с ним угол, размер которого при достаточном удалении от перпендикуляра становится сколь угодно малым. Напротив, с приближением точки О к N размер этого угла неограниченно приближается к d. Угол этот, таким образом, представляет собой однозначную функцию расстояния ON. Обозначая это переменное расстояние через х, Лобачевский обозначает угол параллельности через П (х). Предыдущие соображения, таким образом, сводятся к следующему:

П(х) есть однозначная функция аргумента х, постоянно убывающая при возрастании х; когда х возрастает неограниченно (стремится к бесконечности). П(х) стремится к нулю; когда х стремится к нулю, П(х) стремится к d.

При посредстве этой именно функции Лобачевский выражает тригонометрические уравнения, связывающие стороны и углы треугольника. Место теоремы синусов занимает здесь соотношение

а место теоремы косинусов – соотношение

Эти соотношения легко преобразовываются таким образом, что по любым трем элементам треугольника (из числа сторон и углов) определяют все остальные. В частности для прямоугольного треугольника, в котором а и b суть катеты, а с – гипотенуза, они принимают вид:

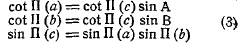
Последнее соотношение, таким образом, заменяет пифагорову теорему евклидовой геометрии. Однако, действительно осуществить решение треугольника, т. е. действительно вычислить элементы треугольника по данным значениям трех из них, с помощью этих уравнений было бы возможно только в том случае, если бы функция П(х) была нам известна, т. е. если бы мы умели определить ее значение по значению аргумента х и обратно. Пока этого нет, пока функция П(х) остается неизвестной, эти уравнения носят только схематический характер. Перед Лобачевским стояла, таким образом, задача эту функцию разыскать, и он с ней справился. Тонким анализом, сущность которого здесь вряд ли возможно изложить, он приходит к заключению, что

Число R в правой части есть постоянная, имеющая положительное значение. Допустим, что значение этой постоянной было бы нам известно. Тогда ясно, что предыдущее соотношение давало бы нам возможность по данному значению аргумента х разыскать соответствующее значение функции П(х), и обратно. Вместе с тем ожили бы приведенные выше тригонометрические уравнения и дали бы возможность реально, по данным значениям трех элементов треугольника, определять остальные. Какое же значение имеет эта постоянная R? Ответ на этот вопрос представляет собой наиболее глубокий из выводов Лобачевского. Он заключается в том, что теоретически, принципиально или, лучше сказать, формально константа R может иметь совершенно произвольное значение. Фиксировав это значение, мы получим определенную геометрическую систему с определенными метрическими соотношениями  средствами которой мы можем оперировать столь же свободно, как и в евклидовой геометрии. Каждому значению R соответствует своя геометрия. Геометрия положения, так сказать, во всех этих системах одна и та же; но количественные соотношения меняются от одной к другой в зависимости от значения постоянной R. Геометрическая система Евклида, таким образом, не единственная. Каждому значению R отвечает до некоторой степени другая система. Если бы дать свободный полет фантазии и представить себе различные миры, в каждом из которых эта константа имеет другое значение, то геометрия каждого пространства определялась бы значением этой константы. В соответствии с этим этой постоянной присвоено название радиуса кривизны пространства, а число – 1/R² называется кривизной пространства. Это  находится в согласии с тем, что кривизна сферы радиуса R выражается числом 1/R²; здесь только взят знак минус. Причины, к этому приводящие, будут указаны ниже; покамест эта терминология выясняет, почему пространство, в котором имеет место  геометрия Лобачевского, принято называть пространством постоянной отрицательной кривизны. Из иных соображений — может быть, менее подходящих — систему Лобачевского принято также называть гиперболической геометрией.

Если мы себе представим, что в соотношении (4), при определенном значении х, R возрастает, то вместе с ним возрастет и угол П(х), приближаясь к прямому. Иными словами, угол параллельности, соответствующий данному отрезку х, тем больше,  тем ближе к прямому углу, чем больше R, т. е., чем меньше по абсолютной величине кривизна пространства. Когда R обращается в ∞, кривизна пространства превращается в 0. В соотношении (4) правая часть обращается в 1 и, следовательно, П(х)  обращается в постоянную, в прямой угол. Эго означает следующее; если кривизна пространства обращается в 0, и из точки О проведен перпендикуляр ON к прямой АВ, то прямая, проходящая через О параллельно к АВ, всегда перпендикулярна к ON, как это имеет место в евклидовой геометрии.

Вместе с тем вся геометрия переходит евклидову. Формально, таким образом, существует бесчисленное множество геометрических систем, одной из которых является геометрия Евклида. Она представляет собой предельный и простейший частный случай. Более того, если обе части в каждом из тригонометрических уравнений (3) развернуть в ряды по возрастающим степеням отношений a/R, b/R, c/R и сохранить только первые члены этих отношений, то мы получим соотношение евклидовой геометрии. Пренебречь высшими степенями отношений a/R, b/R, c/R и сохранить только первые члены этих отношений, то мы получим соотношение евклидовой геометрии. Пренебречь высшими степенями этих отношений можно только в том случае, когда они очень малы, т. е., когда стороны треугольника АВС очень малы по сравнению с R. Это значит: в гиперболическом пространстве, какова бы ни была его кривизна, метрические соотношения тем даже подходят к евклидовым, чем меньше размеры фигуры. Это приводит Лобачевского к мысли, что вера в евклидову геометрию, быть может, представляет собой иллюзию, вызванную тем, что мы обитаем в ничтожном уголке мирового пространства, в пределах которого линейные размеры совершенно незначительны по сравнению с радиусом кривизны пространства.

Располагая тригонометрией гиперболического пространства и соотношением (4), Лобачевский имеет возможность установить всю его метрику, имеет возможность производить измерение длин, площадей и объемов, имеет возможность развить аналитическую геометрию. Новая геометрическая система получает весь тот обхват, всю ту ширь, которую имела классическая геометрия. Произвольный же параметр, характеризующий кривизну, придает системе неизмеримо большую мощность, и евклидова геометрия получает в ней скромное место, как уже сказано, предельного частного случая.

Система, построенная Больай, не так детально разработана, как у Лобачевского; ко многим вопросам он подходит другими методами, другими путями. Но по существу это вполне та же самая система.

7. Интерпретация неевклидовой геометрии. Творцы неевклидовой геометрии — Гаусс, сохранивший свои идеи в строгой тайне, Лобачевский и Больай — имели глубокое убеждение в том, что эта геометрическая система логически так же совершенна, как и система Евклида, и никаких противоречий в себе не содержит. Эго убеждение овладевает всяким, кто изучит основные работы Лобачевского и Больай. Но изучить их не легко; даже Гаусс, которому эти идеи были так близки, говорил, что работы Лобачевского представляют собой непроходимые дебри. Людям же, далеким от этого своеобразного миросозерцания, все эти идеи вообще казались неприемлемыми, даже нелепыми, а тяжеловесные рассуждения Лобачевского усиливали это впечатление. Гаусс достаточно прозорливо предусмотрел, что этот глубокий переворот в области столь установившейся доктрины, как геометрия, вызовет отрицательное к себе отношение. Так оно и случилось. Немногие читали работы Лобачевского, а те, которые читали, либо издевались над его идеями, либо оставили их совсем без внимания. Они долго не получали ни признания, ни распространения. Для обоих творцов неевклидовой геометрии молчание Гаусса и пренебрежительное отношение остального математического мира к их творению, величие которого они явственно ощущали, было источником глубокой жизненной трагедии. Но Лобачевский тщательно искал   для самого себя неопровержимого доказательства логической правильности новой геометрии. Как ни твердо было его субъективное убеждение в том, что неевклидова геометрия никаких противоречий в себе не содержит, для ученого, не предубежденного ни в ту, ни в другую сторону, все же оставался открытым вопрос, не приведет ли в дальнейшем развитии, конца которому нет, новая геометрия к противоречию. Лобачевский искал строгого доказательства того, что это невозможно, что его геометрия логически не менее безупречна, чем евклидова. Он подходит к этой задаче с различных сторон. Главным доводом в его глазах является применение неевклидовой геометрии к вычислению определенных интегралов. Идея заключается в том, что вычисляемый интеграл трактуется как некоторая площадь, или объем, или масса в гиперболическом пространстве. Эта точка зрения дает возможность вычислить значение интеграла средствами неевклидовой геометрии; а затем интеграл вычисляется независимо от неевклидовой геометрии, и результат неизменно получается тот же самый. Подходит он к тому же вопросу и с других точек зрения, и по существу его рассуждения почти имеют доказательную силу; но они не доделаны, не досказаны, пожалуй, не додуманы. Лобачевский унес с собой в могилу только субъективное убеждение в логической правильности созданной им системы; строго установить ее незыблемую логическую достоверность было дано наследникам его научного достояния.

Все пути к этому, в настоящее время разнообразные, основываются на интерпретации неевклидовой геометрии. Это есть новая идея, которая в своем развитии привела к глубокому перевороту во взглядах на существо и значение геометрии. Это — тот источник, из которого был пролит яркий свет на теоретические основания математики.

Точкой отправления здесь служат соображения, с которыми мы уже встречались выше. Нам приходилось уже говорить о том, что различные поверхности имеют свою геометрию. Планиметрия есть геометрия плоскости, сферика есть геометрия шаровой поверхности, и, как было уже выяснено выше, основными образами на плоскости служат точки и прямые линии, на сфере — точки и окружности больших кругов. Планиметрия изучает, прежде всего, углы и фигуры, ограниченные прямыми линиями; сферическая геометрия изучает углы и фигуры, ограниченные окружностями больших кругов. Что сближает между собой окружности больших кругов на сфере и прямые на плоскости? Дуга окружности большого круга на сфере представляет собой кратчайшее расстояние между двумя точками, совершенно так же, как отрезок: прямой представляет собой кратчайшее расстояние на плоскости. Но на каждой поверхности существуют линии, представляющие собой кратчайшие пути, по которым на этой поверхности можно пройти от одной точки к другой. (Некоторые особенные поверхности, с которыми дело обстоит в этом отношении не вполне благополучно, оставим в стороне). Такие линии называются геодезическими линиями поверхности; прямые суть геодезические линии на плоскости, окружности больших кругов — геодезические линии на сфере. Основные линии, которыми оперируют плоская и сферическая геометрия, суть геодезические линии соответствующей поверхности. Отсюда, естественно, возникает вопрос, нельзя ли в том же порядке идей: строить геометрию на любой другой поверхности, принимая за основные образы: точки и геодезические линии этой поверхности. Однако, на пути осуществления этой идеи стоит одно препятствие, о котором мы тоже уже выше упоминали. Как плоская, так и сферическая геометрия оперируют методом наложения, находяшим себе  на этих поверхностях применение благодаря тому, что как на плоскости, так и на  сфере любая часть поверхности может по ней совершенно свободно передвигаться без растяжений, без изгибов, без складок, вообще без всякой деформации. Возможность, таких движений составляет основную презумпцию при построении геометрии; в том порядке идей и методов, в каком строятся плоская и сферическая геометрии, можно развивать геометрию только на таких поверхностях, на которых передвижение фигур без деформации возможно с той же свободой, как на плоскости и на сфере: без этого нельзя говорить о равных отрезках; о больших и меньших отрезках; о равных, больших и меньших углах; о конгруэнтных треугольниках и т. д. Вообще без возможности производить эти движения нельзя оперировать теми понятиями, которыми, можно сказать, проникнуты все предложения плоской и сферической геометрии. Но, кроме плоскости и сферы, в евклидовом пространстве нет поверхности, на которой было бы возможно свободное передвижение частей. Поэтому, плоскостью и сферой, по существу, исчерпываются те поверхности евклидова пространства, на которых можно развивать — методом наложения — двумерную геометрию их геодезических линий и геодезических фигур. Идея исчерпана тем, что классическая геометрия: уже дала. В гиперболическом пространстве, как мы видели, дело обстоит более благоприятно. Там существует еще так называемая предельная поверхность, на которой возможны передвижения фигур с теми же степенями свободы, как на плоскости и на сфере. Геодезическими линиями служат предельные линии. Благодаря этому в гиперболическом пространстве можно развивать геометрию методом наложения еще на предельной поверхности. Мы видели, каким обильным источником идей это обстоятельство послужило для Лобачевского и Больай. В гиперболической поверхности есть также еще один тип поверхностей, на которых возможно построение геометрии в том же порядке идей; это так называемые поверхности равных расстояний. Но геометрия этих поверхностей формально совпадает с геометрией гиперболической плоскости.

Итак, если принять правильной геометрию Лобачевского, то в гиперболическом пространстве имеется троякого типа двумерная геометрия: гиперболическая — это геометрия плоскости (и поверхностей равных расстояний), евклидова, или, как ее иначе называют, параболическая, и сферическая — геометрия сферы. Возвращаясь, однако, к евклидову пространству, мы вновь должны указать, что здесь есть только две поверхности, по которым возможны свободные передвижения фигур без деформации: плоскость и сфера; и, сообразно этому, возможны только две двумерные геометрии, развиваемые методом наложения,— плоская и сферическая.

Знаменитый мемуар Гаусса «Disquisitiones generales circa superficies curvas», опубликованный в 1827 г., дал, однако, этим идеям новое направление. В этом мемуаре Гаусс рассматривает поверхность как гибкую пленку. Под изгибанием поверхности он разумеет такую ее деформацию, при которой не происходит растяжение длин нанесенных на ней кривых; это влечет за собой неизменность и углов между кривыми. Обычное изгибание листа бумаги или нерастяжимой материи может служить наглядным представлением об этом геометрическом процессе. Имея кусок материи, мы часто можем ее так изогнуть, чтобы она без растяжений и складок покрыла другую поверхность. Этот процесс называется наложением одной поверхности на другую, или развертыванием одной поверхности на другой. Он сопровождается деформацией, но при этой деформации не меняется ни одна длина, не меняются углы, не образуется ни разрывов, ни складок. Легко понять, что не всякая поверхность может быть развернута на любую другую. Так, поверхность сферы нельзя никоим образом ни развернуть, ни наложить на плоскость. Гауссом поставлен вопрос о том, при каких условиях возможно развертывание одной поверхности на другой. В тесной связи с этим находится вопрос, представляющий собой частный случай предыдущего.

Если мы вырежем кусок поверхности обыкновенного круглого конуса, то путем его изгибания его можно передвинуть в любое другое место на том же самом конусе. На конической и на цилиндрической поверхности, таким образом, возможно передвижение частей поверхности, сопровождаемое, правда, деформацией, но такой деформацией, которая сводится только к изгибанию. Но это возможно не на всякой поверхности. С поверхности трехосного эллипсоида, например, нельзя срезать куска, прилегающего к вершине меньшей оси, и передвинуть его к вершине большей оси, или наоборот; попытка сделать это неизбежно поведет к разрывам или складкам, на передвигаемой фигуре.

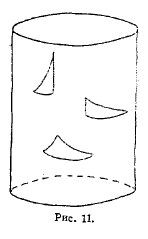
Рис. 11.

Возьмем поверхность, на которой такого. рода движения возможны, — скажем, поверхность круглого цилиндра. Условимся называть две фигуры на поверхности цилиндра, конгруэнтными, если они могут быть приведены в совмещение путем такого передвижения одной из них по поверхности цилиндра, т. е. передвижения, сопровождаемого изгибанием поверхности. На рис. 11 изображены три криволинейных треугольника. В обычном смысле слова треугольники эти не конгруэнтны, ибо наложить один на другой без деформации невозможно; но в новом, расширенном значении этого слова, т. е. путем наложения, сопровождаемого изгибанием, такое совмещение возможно, и потому в новом смысле слова эти три  треугольника конгруэнтны.

Ясно, что при этом новом понимании идеи наложения расширится число поверхностей, на которых можно строить геометрию, пользуясь методом наложения. Конические и цилиндрические поверхности представляют собой простейшие примеры таких, поверхностей. Разберемся в том, какова будет геометрия цилиндра; для этого обратим внимание на то обстоятельство, что цилиндрическую поверхность можно образовать путем свертывания плоскости, или что на цилиндрическую поверхность можно навернуть плоскость. Геодезическими линиями на цилиндрической поверхности будут служить те кривые, по которым расположатся прямые плоскости. Если представим себе вертикальный круглый цилиндр и вертикальный кусок плоскости, то при  навертывании последней на цилиндрическую поверхность вертикальные прямые останутся прямыми линиями, горизонтальные свернутся в окружности, а наклонные изовьются в винтовые линии различного хода. На рис. 11 в среднем из трех изображенных на нем прямоугольных геодезических треугольников один катет образован отрезком прямой линии, другой – дугой окружности, а третий — дугой винтовой линии. Легко понять, что формально по своему содержанию, еще точнее — по словесному своему выражению, геометрия такого цилиндра совпадает с геометрией той части плоскости, которая на этот цилиндр навертывается: фигурам, конгруэнтным на этой части плоскости, будут отвечать фигуры, конгруэнтные на поверхности цилиндра, и геометрия круглого цилиндра в целом будет отличаться от геометрии плоскости по двум причинам: во-первых, на цилиндр навертывается не вся плоскость, а только часть ее, во-вторых – края навертываемой на цилиндр прямоугольной полосы сходятся: благодаря этому горизонтальные геодезические линии становятся замкнутыми и имеют конечную длину.

Если мы, однако, вместо круглого цилиндра возьмем цилиндр с бесконечной образующей, то мы получим поверхность, на которой целиком осуществляется евклидова геометрия. Для большей определенности вообразим себе параболу на горизонтальной плоскости и вертикальную образующую, скользящую по этой параболе (рис. 12). Она образует бесконечную разомкнутую цилиндрическую поверхность. При навертывании на нее вертикальной плоскости вертикальные прямые останутся прямыми, горизонтальные изогнутся в параболы, а наклонные примут вид параболических винтов. Геодезические линии, таким образом, здесь будут иметь различные формы, но все они будут бесконечны, и через две точки всегда будет проходить только одна геодезическая линия. Вместе с тем геометрия на поверхности параболического цилиндра будет полностью совпадать с геометрией плоскости. Каждое предложение евклидовой планиметрии будет здесь справедливо, но только под прямыми линиями здесь нужно будет разуметь геодезические линии поверхности.

Рис. 12.

Эти результаты поучительны в двояком отношении: во-первых, они, как уже указано, умножают число поверхностей, на которых можно развивать геометрию теми же методами, которыми строится геометрия Евклида. Во-вторых, и это, может быть, еще важнее, мы уясним себе, что евклидова планиметрия получает осуществление не только на плоскости. Подробнее: если мы оголим словесный текст евклидовой планиметрии, то содержание ее может оказаться справедливым при различном понимании терминов, в этот текст входящих.

Она будет справедлива, если под прямыми   разуметь обыкновенные прямые на плоскости, под углами — обыкновенные прямолинейные углы, под движением — перемещение фигуры по плоскости без деформации. Но все те же предложения будут  справедливы и в том случае, если под прямыми разуметь геодезические линии на параболическом цилиндре, под углами — криволинейные углы, этими геодезическими   линиями образуемые, под движением — передвижение фигур на параболической поверхности, сопровождаемое их изгибанием.

Всякую систему образов, которую можно разуметь под терминами геометрии, мы будем называть интерпретацией этой геометрии, или формой ее осуществления. Вывод, к которому мы выше пришли, мы   можем формулировать, следовательно, такими словами: евклидова планиметрия допускает различные интерпретации, различные формы осуществления.

Если мы примем во внимание, что евклидова планиметрия получит осуществление   на любой поверхности, на которую плоскость может быть навернута, то мы легко   представим себе, сколь многообразными   могут быть эти различные формы осуществления, - эти интерпретации евклидовой планиметрии.

8. Геометрия поверхностей постоянной кривизны. Возвратимся теперь к вопросу о том, на каких поверхностях возможно передвижение фигур, сопровождаемое изгибанием. Некоторое затруднение в уяснении ответа на этот вопрос представляет понятие о кривизне поверхности в данной  точке, установленное Гауссом. Мы хорошо себе представляем, что поверхность может  быть более искривлена в одних своих точках и менее в других. Одна из главных  заслуг Гаусса в геометрии заключается в том, что он дал средства для точного численного выражения меры кривизны поверхности в каждой ее точке.

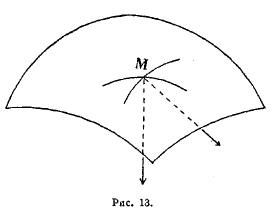
Рис. 13.

Точку М на поверхности фигуры обведем небольшой замкнутой линией. Обрадуется замкнутая площадка, ограниченная этой линией. Вдоль всей линии проведем  к поверхности нормали (перпендикуляры),  которые, таким образом, окружат нашу площадку. Размер этой площадки обозначим через s. Теперь из какой-нибудь точки пространства радиусом, равным единице длины, опишем сферу и из ее центра проведем радиусы, параллельные всем нормалям, ограничивающим площадку s. Эти нормали выделят на сфере некоторую площадку σ. Легко понять, что размеры этой площадки зависят от того, в какой мере поверхность изогнута вокруг точки М. Если поверхность плоская, т. е. если она совсем не изогнута, то все перпендикуляры параллельны, а параллельные им радиусы вспомогательной  сферы сольются в один, — вместо площадки σ мы получим одну только точку; иначе говоря, σ в этом случае равно 0: Если поверхность вокруг точки М будет слабо изогнута, то площадка σ будет очень мала;  напротив, если поверхность будет значительно изогнута вокруг точки М, то нормали образуют большой раструб, благодаря чему на сфере получится большая площадка σ. В соответствии с этим Гаусс принимает за среднюю кривизну поверхности в ограниченном контуре отношение σ/s. Когда контур, охватывающий точку М, становится все меньше и меньше — стремится к 0, то отношение σ/s   стремится к определенному пределу; этот предел Гаусс и  принимает за меру кривизны поверхности в данной точке. Следуя этому правилу, можно легко обнаружить, что кривизна шаровой поверхности радиуса R в каждой точке равна 1/R².

Гаусс приписывает кривизне поверхности  в каждой ее точке также знак. Если мы в точке М поверхности проведем нормаль и через нее различные плоскости, то они при пересечении с поверхностью дадут так называемую розетку нормальных сечений. На одних поверхностях все сечения, образующие эту розетку, направлены своею  вогнутостью в одну и ту же сторону; на других поверхностях одни из этих сечений изогнуты в одну сторону, другие — в другую. Так, в точке М сферической поверхности все нормальные сечения обращены вогнутостью в сторону внутренней нормали (на рис. 13 — вниз); на седлообразной же поверхности (например, однополого гиперболоида), изображенной на рис. 14, продольные сечения обращены вогнутостью кверху, а поперечные — вниз. В том случае, когда все сечения направлены вогнутостью в одну сторону, Гаусс приписывает кривизне знак +, а в том случае, когда эти сечения направлены в различные стороны, кривизне приписывается знак — (кривизна имеет отрицательное значение). В каждой точке сферической поверхности кривизна имеет положительное значение, в каждой точке седлообразной поверхности кривизна имеет отрицательное значение.

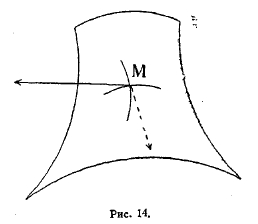
Рис. 14.

Самая замечательная теорема, установленная Гауссом в «Disquisitiones», заключается в том, что при изгибании поверхности кривизна ее в каждой точке сохраняет свое значение. Если поэтому одна поверхность может быть развернута на другую, то в точках, приходящих при этом в совпадение кривизна имеет на одной и другой поверхности одно и то же значение. Теперь мы будем в состоянии ответить на поставленный выше вопрос о том, каковы поверхности, на которых фигура может передвигаться свободно путем изгибания. Ответ этот представлял собой непосредственный вывод из основной теоремы Гаусса и впервые был указан Миндингом. Если поверхность может быть передвинута сама по себе так, чтобы любая ее точка А совпала с любой другой точкой В, то ее кривизна в точке А должна быть такая же, как в любой другой точке В. Иными словами, поверхность должна иметь во всех точках одинаковую кривизну, — короче, как принято говорить, это должна быть поверхность постоянной кривизны. К таким поверхностям, в первую очередь, относится плоскость, кривизна которой во всех точках равна нулю. Постоянную кривизну, равную нулю, имеют также все те поверхности, которые развертываются на плоскость. Сюда относятся, в частности, конические и цилиндрические поверхности, о которых мы говорили выше; на них возможна поэтому геометрия, развиваемая методом наложения; как мы видели, эта геометрия совпадает с евклидовой планиметрией.

Сфера радиуса R имеет постоянную кривизну 1/R² и притом положительную. Но сфера — не единственная поверхность постоянной положительной кривизны; есть бесчисленное множество других поверхностей, которые развертываются на сферу. Если возьмем вырезок сферы, ограниченный двумя меридианами, и свернем его так, чтобы меридиональные края сошлись, то мы получим поверхность веретенообразной формы, имеющую ту же постоянную положительную кривизну. Геометрия такой поверхности, конечно, совпадает с геометрией той части сферы, свертыванием которой эта поверхность получена. Сгибая те или иные части сферы, можно получить поверхности самой причудливой формы, и на всех них будет иметь место сферическая геометрия.

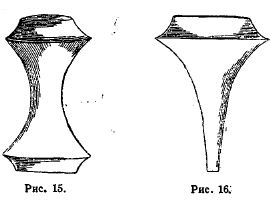
Рис. 15. 16.

Но, согласно теории Гаусса-Миндинга, свободное передвижение фигур путем изгибания возможно также на поверхностях постоянной отрицательной кривизны. Этого рода поверхности в первый раз исследовал Миндинг; он построил их тригонометрию, т. е. построил уравнения, связывающие стороны и углы геодезического треугольника на поверхности постоянной отрицательной кривизны. По игре случая этот мемуар Миндинга и мемуар Лобачевского, содержавший тригонометрию неевклидовой плоскости, были помещены в двух последовательных томах  журнала Креля («Journal für reine und angewandte Mathematik», Bd. XIX, Bd. XX). Но  только через 30 лет Бельтрами (см.) обнаружил связь между этими работами. Бельтрами, впрочем, вел свои исследования совершенно независимо от Миндинга. Он изучал различные поверхности постоянной отрицательной кривизны, исследовал их геометрию и тригонометрию. Он был знаком с работами Лобачевского и с величайшим изумлением и торжеством обнаружил, что геометрия поверхностей постоянной отрицательной кривизны формально совпадает с геометрией неевклидовой плоскости, совладает в том же смысле, в каком геометрия цилиндра совпадает с геометрией евклидовой плоскости, а геометрия поверхностей постоянной положительной кривизны совпадает с геометрией сферы. Бельтрами, а за ним Дини привели примеры различных поверхностей постоянной отрицательной кривизны, в особенности тех из них, которые могут быть получены путем вращения. На рис. 15 и 16 изображены такого рода поверхности; из них поверхность (рис. 16), имеющая вид бесконечно суживающегося бокала, особенно замечательна; ее обыкновенно называют псевдосферой (некоторые авторы называют псевдосферой всякую поверхность отрицательной кривизны). Впечатление, произведенное мемуарами Бельтрами, было огромное. Планиметрия Лобачевского ожила: она утратила характер остроумного парадокса, она оказалась геометрией реальных образов.

Весь результат, к которому мы пришли, можно  формулировать теперь следующим образом. Если на передвижение фигур по поверхности смотреть с широкой точки зрения Гаусса, то существуют три типа двумерных геометрий. Во-первых, геометрия поверхностей, развертывающихся на плоскость, или иначе, поверхностей постоянной нулевой кривизны; это есть евклидова планиметрия; из соображений, в которые здесь нецелесообразно входить, ее называют также параболической геометрией. Во-вторых, геометрия поверхностей постоянной положительной кривизны; эта геометрия формально не отличается от геометрии сферы; ее в настоящее время часто называют эллиптической геометрией. В-третьих, наконец, геометрия поверхностей постоянной отрицательной кривизны; эта геометрия формально совпадает с планиметрией Лобачевского; ее в настоящее время часто называют, как мы уже сказали, гиперболической геометрией.

Казалось бы, что после этого замечательного открытия Бельтрами вопроса о логической правильности геометрии Лобачевского не могло более существовать. Нужно сказать, что с этого времени ни один геометр, бывший в курсе дела, в этом действительно уже не сомневался. Но, с точки зрения строгой логики, вопрос все-таки нельзя было считать решенным, и это по двум причинам. Во-первых, исследования Бельтрами могли решить судьбу только двумерной гиперболической геометрии; вопрос же о трехмерном гиперболическом пространстве оставался совершенно открытым. Во-вторых, и по отношению к двумерной гиперболической геометрии оставались серьезные сомнения. Гиперболическая геометрия на всех известных нам формах псевдосферы осуществляется лишь частично, подобно тому, как плоская евклидова геометрия лишь частично осуществляется на поверхности круглого цилиндра. Чтобы достигнуть полного осуществления евклидовой геометрии, мы должны были перейти к параболическому цилиндру, вообще к такой цилиндрической поверхности, на которой все геодезические линии имеют бесконечное протяжение.

Сообразно этому, для полного осуществления гиперболической геометрии необходимо было бы найти такую поверхность постоянной отрицательной кривизны, на которой все геодезические линии имели бы бесконечное протяжение. Такую поверхность тщательно искали, но ее не нашли. Более того: Гильберт показал, что такого рода поверхности вовсе не существует. Пытливый ум геометра-логика на этом не успокоился. Нужно было довести решение вопроса до конца; это было достигнуто дальнейшим развитием идеи об интерпретации геометрии.

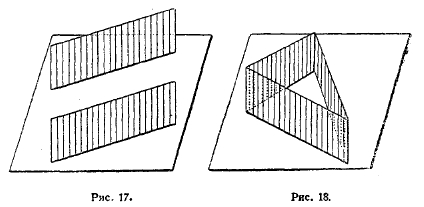
Рис. 17. 18.

9. Свободная интерпретация геометрии. В предыдущих двух главах были установлены две основные идеи. Первая из них заключается в том, что геометрическая система может получать различные интерпретации, или различные формы осуществления. Вторая дает такого рода интерпретацию неевклидовой геометрии в евклидовом пространстве.

Если мы возвратимся к интерпретациям евклидовой планиметрии, данным в предыдущей главе, то заметим, что они сводились всегда к тому, что под прямой линией разумели геодезическую линию на той или иной поверхности. Движение же фигур без деформации заменялось таким их движением, которое сопровождается изгибанием. В этом направлении можно, однако, идти и дальше. Можно значительно больше оторвать геометрические термины от тех образов, которые мы с ними первоначально соединили, не нарушая правильности, справедливости или применимости самой системы.

Вообразим себе горизонтальную плоскость в евклидовом пространстве. Над каждой точкой этой плоскости представим себе, по одну и ту же сторону от плоскости, перпендикуляр одной и той же длины. Над каждой точкой плоскости будет стоять, таким образом, перпендикулярный стерженек. Теперь под «точкой», в новом значении этого слова, будем разуметь каждый такой стерженек. Под «прямой» будем разуметь плоскую полоску, имеющую ширину, равную высоте стерженька и проходящую через два таких стерженька. Таким образом, «прямая» будет составлена из точек-стерженьков, стоящих над обыкновенной прямой в плоскости основания. Легко видеть, что через две «точки» проходит одна и только «одна «прямая», что «прямая» может быть неограниченно продолжена и т. д. Рис. 17 изображает две параллельные «прямые», а рис. 18 — «прямолинейный треугольник». Совершенно ясно, что и при этой интерпретации, уводящей нас уже далеко от обычных точек и прямых, евклидова планиметрия все-таки остается справедливой.

В этом направлении можно идти еще много дальше. Приведем чрезвычайно замечательный и простой пример, принадлежащий Пуанкаре (см.). Возьмем обыкновенную евклидову плоскость Q и в ней точку О. Эту последнюю точку как бы изымем из плоскости, т. е. под «плоскостью», которой мы будем заниматься теперь, мы будем разуметь совокупность всех точек плоскости Q, за исключением точки О; этой последней в нашей плоскости Q не существует.

Теперь под «прямой», в новом значении этого слова, будем разуметь каждую окружность и каждую прямую, проходящую через точку О. Можно представлять себе, что точка О для обитателей «плоскости» недостижима и представляется им бесконечно удаленной. При этих условиях через каждые две «точки» будет проходить «прямая»: в самом деле, если точки А и В лежат на одной прямой с О, то проходящая через них прямая будет служить «прямой» и в новом значении этого слова. Если же точки А и В не расположены на одной прямой с точкой О, то через них можно провести одну и только одну окружность, проходящую через точку О. Эта окружность и будет служить в нашей новой «плоскости» «прямой», проходящей через точки А и В. Ясно, что каждую ограниченную «прямую» можно продолжить в обе стороны, и для обитателя, для которого точка О представляется бесконечно удаленной, это продолжение можно производить неограниченно. Какие «прямые» будут в этой геометрии параллельными? Если эти две «прямые» представляют собой также прямые в обычном смысле слова, то они всегда будут параллельны, так как сходятся в точке О и потому в нашей «плоскости», в новом значении этого слова, они общей точки не имеют: они встречаются только в бесконечно-удаленной точке. Если одна из них — прямая в обычном значении слова, а другая есть окружность, проходящая через точку О, то эти «прямые» параллельны, когда прямая касается окружности в точке О: эти «прямые» не имеют общей точки, ибо точка О в новой плоскости не существует. Точно так же, две «прямые», представленные двумя окружностями, параллельны, если эти окружности в точке О соприкасаются.

Положим теперь, что А и В суть две «точки» нашей «плоскости»; через них проходит «прямая» АВ. Пусть С будет «точка» нашей «плоскости», лежащая вне «прямой» АВ; ясно, что через «точку» С проходит одна и только одна «прямая», параллельная «прямой» АВ. Если, например, «прямая» АВ осуществляется окружностью, проходящей через точку О, то этой параллелью будет служить окружность, проходящая через «точку» С и касающаяся первой окружности в точке О. Такая окружность существует только одна. Легко понять, таким образом, что двумерная геометрия, в которой «прямые» имеют такую своеобразную форму, все-таки будет представлять собой обыкновенную евклидову планиметрию.

Впрочем, один вопрос требует тщательного выяснения. Что представляет собой движение в этой своеобразной геометрии? Уяснить себе вполне решение этого вопроса, значит овладеть последней позицией в деле современной постановки теоретического обоснования геометрии.

10. Сопряжение многообразий. Одну из наиболее важных, основных идей современной математики представляет понятие о сопряжении, или преобразовании. «Одну из важнейших особенностей нашего духа», говорит Р. Дедекинд, «представляет собою способность относить одну вещь к другой вещи». Этот процесс, выработавшийся в эволюции нашей психической деятельности; принято называть ассоциацией. В математике он получает, как и все математические операции, более точную формулировку. Так как он имеет коренное значение при теоретическом обосновании, как геометрии, так и арифметики, то мы должны очень отчетливо выяснить его сущность.

Всякую совокупность некоторых объектов, однородных в том смысле, что каждый из них рассматривается только как элемент этой совокупности, называют в математике комплексом (Komplex, ensemble), многообразием (Mannigfaltigkeit), или множеством (Menge). Совокупность всех целых чисел есть множество; совокупность всех простых чисел, совокупность всех рациональных дробей — все это суть множества. В геометрии линии, поверхности, тела можно рассматривать, как множества, составленные из точек. В окружающей нас обстановке мы можем рассматривать как множество любую группу вещей, если мы отвлекаемся от особенностей каждой из них и сосредоточиваем наше внимание на ее принадлежности к этой совокупности — к этому множеству. Множества мы будем обозначать немецкими прописными буквами, их  элементы — латинскими. Положим, что мы имеем два множества: А с элементами А, А1, А2,… — и множество  B с элементами В, В1, В2,… Тогда мы можем устанавливать сопряжения, или соответствия, между элементами обоих множеств. Привести множество А в сопряжение, или в соответствие, с множеством В — значит признать каждый элемент множества А соответствующим некоторому элементу множества  B; при этом необходимо точно установить, какому именно элементу множества В соответствует каждый элемент множества А. Множество А может состоять, скажем, из тетрадей, множество В — из учеников. Мы можем установить относительно каждой тетради А, какому ученику В она соответствует (принадлежит). Если такое распределение установлено так что каждая тетрадь действительно отнесена некоторому ученику, то в математической терминологии это означает, что множество А (тетрадей) приведено в сопряжение, или в соответствие, с множеством В (учеников). При этом может, конечно, оказаться, что несколько тетрадей будут отнесены (присвоены) одному и тому же ученику; может оказаться, что тетрадей не хватит на учеников; но может оказаться и так, что каждая тетрадь будет присвоена одному ученику, и на каждого ученика придется одна тетрадь. В этом последнем случае говорят, что множество А приведено с множеством В в совершенное сопряжение. Такого рода процесс совершенного сопряжения представляет собой так называемое нумерование. Если мы имеем множество, состоящее, скажем, из пяти объектов, и отмечаем эти объекты номерами 1, 2, 3, 4, 5, то процесс этот заключается в установлении совершенного сопряжения, или соответствия, между множеством наших объектов и множеством чисел 1, 2, 3, 4, 5. Такого рода процессы сопряжения, или соответствия, мы осуществляем на каждом шагу.

Положим, что некоторое общество, собравшееся для игры, состоит из двух групп одинаковой численности, и по характеру игры каждое лицо одной группы должно иметь партнера из другой группы. Чтобы это осуществилось, должно состояться соглашение, которым фактически будет установлено совершенное сопряжение между обеими группами игроков. Положим, далее, что каждым игроком ставится определенная ставка и, естественно, может состояться соглашение, по которому каждый игрок выбирает себе такого партнера, который ставит ту же ставку, что и он. Теперь с каждым участником нашей игры (с каждым элементом того и другого множества) связано некоторое число, выражающее размер его ставки. Сопряжение между обеими группами (множествами) установлено так, что эта ставка (число) остается неизменной (инвариантной) при переходе от элемента одной группы к соответствующему элементу второй группы. В математической терминологии это выражают так: при установленном сопряжении между двумя множествами, каждый элемент имеет инвариант.

Положим теперь, для простоты, что каждая группа состоит из трех игроков: первая из игроков: А со ставкой в 5 руб., А' — со ставкой в 9 руб. и А'' — со ставкой в 13 руб.; вторую группу составляют: В со ставкой в 2 руб., В' — со ставкой в 6 руб. и В'' — со ставкой в 10 руб. Составить теперь сопряжение с инвариантной ставкой, очевидно, невозможно. Положим, однако, что сопряжение состоялось. А выбрал себе партнером В, А' выбрал В', а А'' выбрал В''. Элементы сопряжения в отдельности инварианта не имеют. Но если мы возьмем двух каких-нибудь игроков первой группы, А и А', А’ и А'' или А и А'', и составим соответствующие пары второй группы, то окажется, что разность ставок каждой пары всегда та же, что и разность ставок соответствующей пары во второй группе (она равна 4 для первой и второй пары и 8 для третьей пары). Это выражают математически так: в рассматриваемом сопряжении инвариант имеют каждые два элемента; это есть разность ставок двух игроков. Можно было бы указать примеры, когда инвариант имеют не менее чем три элемента; бывают случаи, когда инварианты имеют как одиночные элементы, так и составленные из них пары, тройки и т. д.

Мы говорили до сих пор все время о совершенном сопряжении одного множества с другим. Но второе множество может иногда совпадать с первым; тогда устанавливается сопряжение многообразия с самим собой. Оно заключается в том, что каждому элементу множества мы относим в качестве соответствующего, ему некоторый элемент того же множества.

Группа игроков располагается в кружок. Каждый из них по содержанию игры несет определенные обязанности по отношению к другому участнику игры. В простейшем случае этим коллегой является его сосед справа (игра так и называется, «в правого соседа»). Сущность дела сводится к тому, что игра каждому участнику (каждому элементу множества)  относит другого участника (другой элемент множества); этим устанавливается совершенное сопряжение группы игроков с самой собой (множества с самим собой). И в этом сопряжении возможны инварианты одного, двух или нескольких элементов.

Мы остановимся еще на одном очень важном понятии. Положим, что мы имеем некоторое множество В. Мы в нем можем, устанавливать различные сопряжения с самим собой. Эти различные сопряжения будем обозначать через S, S', S'',... Мы можем, таким образом, говорить о совокупности сопряжений одного и того же множества с самим собой. Одна и та же группа игроков может при игре в соседи различным образом рассаживаться в кружок, и каждое такое перераспределение отводит каждому игроку другого соседа, — устанавливает другое сопряжение многообразия с самим собой. Положим, что одно из совершенных сопряжений S относит произвольному элементу А элемент А', а другое сопряжение S' относит элементу А' элемент А''. Теперь отнесем элементу А в качестве соответствующего элемент А''. Этим мы снова установим некоторое совершенное сопряжение многообразия с самим собой. Говорят, что это новое сопряжение составлено из сопряжений S и S', или что оно заменяет последовательное производство сопряжений S и S'. Чтобы выяснить это на примере, положим, что в некоторой игре каждый игрок получает кость; первый тур игры заключается в том, что каждый игрок А передает свою кость избранному им игроку А', причем ни одному игроку не разрешается принять кость от двух участников игры. Когда этот тур закончен, каждому игроку А соответствует (отнесен) другой игрок А', которому он передал свою кость; этим произведено сопряжение S множества игроков с самим собой. Далее совершается второй тур в таком же порядке, причем и теперь каждый игрок свободно выбирает партнера, которому он в этот раз передает свою кость. Этим будет осуществлено новое сопряжение S' множества игроков с самим собой; в этом сопряжении игроку А' будет соответствовать игрок А''. Кость, находившаяся в начале игры у игрока А, после второго тура перейдет к А''. Если мы теперь каждому игроку А в качестве соответствующего отнесем игрока А'', получившего его кость после второго тура, то этим в множестве игроков будет вновь установлено сопряжение, или соответствие, S'', которое заменяет последовательное производство сопряжений S и S', или составлено из сопряжений S и S'. Это новое сопряжение обозначают обыкновенно символом SS'. Если бы каждый игрок А получил обратно кость, которую он имел в начале игры, и сам сразу передал бы ее тому партнеру А'', который ее получил во втором туре, то он, так сказать, непосредственно осуществил бы то сопряжение, которое заменяет последовательное производство сопряжений S и S’.

В связи с этим остается выяснить еще одно понятие. Как из предыдущих примеров должно быть ясно, в каждом множестве можно устанавливать различные его сопряжения с самим собою. Пусть S1, S2, S3,..., Sk будут некоторые сопряжения множества А с самим собой. Эту совокупность сопряжений мы обозначим через ∑. Возьмем теперь два сопряжения — S_i и S_j и образуем составленное из них сопряжение S_iS_j. Может оказаться, что это новое сопряжение фигурирует в совокупности ∑, но может случиться, что его в этой совокупности нет. Если совокупность сопряжений ∑ такова, что всякое сопряжение S_iS_j, составленное из двух ему принадлежащих сопряжений, также входит в ее состав, то говорят, что совокупность ∑ составляет группу сопряжений. Если множество А содержит конечное число элементов, то существует определенное число возможных сопряжений этого множества с самим собой. Совокупность всех этих сопряжений, очевидно, составляет группу. Что из той же совокупности можно выделить часть сопряжений, последовательное производство которых может  дать сопряжения, в эту часть не входящие, — это также ясно; в самом деле, если в совокупность ∑ мы введем сопряжения S и S', но не введем сопряжения SS’, то совокупность ∑ группы не образует.

11. Геометрические преобразования и интерпретация геометрического движения. Обратимся теперь к сопряжениям, производимым в геометрических образах. Линию, поверхность, часть пространства и все пространство мы можем рассматривать как многообразие, или множество, состоящее из точек; в таком многообразии мы можем устанавливать сопряжения его с самим собой. Для определенности остановимся на плоскости. Если мы произведем ее сопряжение с самою собой, т. е. каждой ее точке отнесем некоторую другую точку в качестве соответствующей ей, то каждой фигуре будет соответствовать другая фигура, составленная из соответствующих точек. В этом смысле можно сказать, что сопряжение плоскости с самой собой преобразовывает каждую ее фигуру в другую фигуру. По этим соображениям сопряжения геометрического образа с самим собой принято называть геометрическим преобразованием.

Рис. 19.

Приведем примеры простейших геометрических преобразований. Выбрав определенную точку О (рис. 19), отнесем каждой точке А другую точку А', расположенную на луче ОА таким образом, что ОА' = k·OA, где k есть некоторое постоянное положительное число. Можно сказать, что это преобразование относит точке А другую точку А' на луче ОА таким образом, что отношение ОА':ОА остается постоянным (равным k); если k>1, то точка А' более удалена от О, нежели точка А; если k<1, то она ближе к О, чем А. Вследствие этого каждая линия и каждая фигура преобразовывается в подобную линию или в подобную фигуру (например, на нашем чертеже линия AA₁A₂... преобразуется в линию А'А'₁A'₂..; треугольник KLM — в подобный ему треугольник К'L'М'). Сообразно этому, такое преобразование называют подобным преобразованием, или просто подобием, точку О называют центром подобия, а число k — отношением подобия. Возможны различные подобные преобразования из одного и того же центра; они отличаются ото от другого значением числа k — отношения подобия. Если мы возьмем два подобных преобразования с общим центром, одно с отношением подобия k, другое с отношением I, то составленнное из них преобразование есть также подобное преобразование вокруг того же центра с отношением подобия kl; это вполне понятно: если одно преобразование, скажем, увеличивает размеры в k раз, другое их затем увеличивает в I раз — в результате получается увеличение в kl раз. Следовательно, совокупность подобных преобразований из одного и того же центра образует группу. Но два подобных преобразования из различных центров при составлении, вообще говоря, не дают подобного преобразования, произведенного из какого-либо третьего центра; поэтому совокупность всевозможных преобразований из различных центров не образует группы.

Рис. 20.

Рассмотрим следующее, еще более простое преобразование. На плоскости возьмем какой-либо вектор ОО' (рис. 20), т. е. прямолинейный отрезок определенной величины и определенного направления. Из любой точки А проведем вектор АА', равный ОО', т. е. отрезок той же длины и того же направления. Точку А' будем считать соответствующей точке А. Таким же образом точкам В, С, D,... отвечают точки В', С', D',... Каждой точке плоскости, таким образом, отвечает определенная, соответствующая ей точка — этим устанавливается преобразование плоскости. Если бы мы передвинули всю плоскость в направлении ОО' на расстояние ОО', то точки А, В, С, совместились бы с соответствующими точками А', В', С',..., т. е. каждая точка плоскости совместилась бы с соответствующей ей точкой. Вследствие этого такое преобразование называют параллельным перенесением плоскости, а вектор ОО' — вектором перенесения.

Если мы выполним параллельное перенесение с вектором ОО', а затем параллельное перенесение с вектором О'О'', то это будет эквивалентно одному параллельному перенесению с вектором ОО''. Все параллельные перенесения образуют группу, и смысл этого утверждения заключается в том, что два последовательных параллельных перенесения могут быть заменены одним параллельным перенесением.

Рис. 21.

Рассмотрим еще другой пример. Выберем опять произвольную точку О за центр и каждой точке А отнесем другую точку А' следующим образом (рис. 21). Из центра О проведем дугу окружности АА' определенной градусной величины ω определенную сторону (положительную или отрицательную); конечную точку А' этой дуги примем за соответствующую точке А. Таким образом, точкам В, С, D... будут соответствовать точки В', С', D',..., причем дуги ВВ', СС', DD',... все будут иметь ту же угловую величину ω. Легко понять, что при повороте всей плоскости вокруг точки О на угол ω каждая точка М придет в соответствующую ей точку М'. Поэтому самое преобразование называется вращением, или поворотом плоскости вокруг центра О на угол ω. Ясно, что поворот на угол ω и последующий за этим поворот на угол ω' эквивалентны повороту на угол ω+ω'; иными словами, совокупность всех вращений вокруг одного и того же центра образует группу. Замечательно, что совокупность всех вращений плоскости вокруг различных центров также представляет собою группу; мы не будем этого здесь доказывать. Нужно, однако, все же отметить, что движение есть механический процесс, а геометрическое преобразование есть математический акт — отнесение одной точки к другой.

Два последних преобразования имеют ту особенность, что каждое из них осуществляется движением — параллельным перенесением или вращением плоскости. Обратимся теперь к любому движению плоскости в самой себе. Под геометрическим движением мы разумеем нечто, отличное от механического движения в том смысле, что оно не рассматривается как процесс, происходящий во времени. Под геометрическим движением мы разумеем только перемещение того или иного образа из одного положения в другое. Для геометрического движения (в отличие от механического) вопрос о том, как перемещение совершалось — путь, по которому оно шло, не играет никакой роли: важны лишь начальное и конечное положения образа. Два движения различны, если они приводят какой-либо образ в два различных положения; они совпадают, если каждое из них приводит любой образ в то же положение, что и другое (осуществлять это они могли различными путями).

Как известно, положение плоскости в самой себе вполне определено, если известно положение двух ее точек. Точнее, движение плоскости в самой себе вполне определено, если известно, в какие точки оно приводит две определенные точки плоскости. Итак, положим, что некоторое движение S плоскости в самой себе приводит ее точки М и N в совмещение с точками М' и N'. Так как путь, каким это осуществлено, никакого значения не имеет, то мы предположим, что это выполнено следующим образом: сначала произведено параллельное перенесение, приводящее точку М в точку  М'; при этом точка N' пришла в точку N; затем вращением вокруг точки М' точка N приведена в точку N'. Всякое движение плоскости в самой себе может быть рассматриваемо как результат последовательного производства одного параллельного перенесения и одного вращения. Всякое движение плоскости в самой себе осуществляет некоторое геометрическое преобразование, слагающееся из двух элементарных преобразований параллельного перенесения и вращения плоскости¹⁾. Самое существенное в этом то, что всякое движение плоскости в самой себе устанавливает геометрическое преобразование, относящее каждой точке плоскости А в качестве соответствующей ей ту точку А', в которую это движение точку А приводит. Ясно также, что совокупность всех движений плоскости в самой себе образует группу. В самом деле, если некоторое движение S приводит плоскость из одного ее положения в самой себе в другое, а другое движение S’ переводит ее из этого положения в третье, то всегда существует движение, непосредственно приводящее плоскость из первого положения в третье, т. е. заменяющее последовательное производство движений S и S'. Если движение S совмещает некоторый образ B на плоскости с образом B', то это означает, что образ B конгруэнтен образу B'; если другое движение S' совмещает образ B' с образом B'', то это означает, что образ B' конгруэнтен образу B''. Движение SS' (составленное из движений S и S') совмещает образ B с образом B'', т. е. устанавливает, что образ B конгруэнтен образу B''. Иными словами, то обстоятельство, что совокупность движений образует группу преобразований, представляет лишь иное выражение того основного в геометрии положения, что соотношения B = B' и B' = B'' влекут за собою соотношение B = B''.

¹⁾ Можно показать, что каждое движение плоскости в самой себе может быть осуществлено либо с одним параллельным перенесением, либо одним вращением. Мы не будем здесь этого рассматривать.

Мы до сих пор говорили, что движение осуществляет геометрическое преобразование. Мы скажем теперь больше; формально, в строго логической геометрии, движение только и представляет собой геометрическое преобразование; физическое или механическое движение представляет собой конкретное осуществление этого преобразования. В самом деле, в наших геометрических рассуждениях мы постоянно говорим о движении, но фактически никогда его не производим. Следовательно, самый механический процесс движения для нас никакого значения не имеет. Если проследить любое рассуждение, в котором мы в геометрии пользуемся движением, то будет непосредственно ясно, что нас интересует только одно: в какую точку это движение приводит каждую точку плоскости; иными словами, нас интересует только то геометрическое преобразование, которое осуществляется каждым движением. Реальное движение находится в таком же отношении к соответствующему ему геометрическому преобразованию, в каком физическое тело стоит к его геометрическому образу.

Итак, в формальной геометрии совокупность движений фигурирует только как группа геометрических преобразований.

Имеют ли все преобразования этой группы какие-либо инварианты? Легко видеть, что одна точка инварианта не имеет. В самом деле, если бы такой инвариант существовал и, следовательно, имел определенное значение в каждой точке плоскости, то произвольно взятая точка М могла бы быть приведена только в такую точку плоскости М’, в которой инвариант имеет то же значение. Между тем движения на плоскости таковы, что всякую точку М можно привести в любую другую точку М’.

Но две точки имеют инвариант относительно группы движений; этим инвариантом служит расстояние между этими точками. В самом деле, если какое-либо движение приводит точки А и В в совмещение сточками А' и В', то расстояния АВ и А'В' равны между собой. Что касается трех точек, то и они имеют инвариант. В самом деле, тремя точками А, В, С определяется треугольник АВС, вершинами которого они служат; площадь этого треугольника и есть инвариант движения. Но, как известно, площадь треугольника АВС выражается через его стороны, т. е. через расстояния АВ, ВС и АС. Поэтому, по существу, площадь не есть новый инвариант; это есть функция расстояний, она выражается в этих расстояниях. Можно доказать, что ни три точки, ни большее число их не имеет относительно движений независимого инварианта, т. е. не выражающегося через расстояния между точками.

Инвариант, представляющий собой расстояние между двумя точками, имеет две особенности, на которые необходимо обратить внимание. Если, скажем, r есть инвариант какого-либо преобразования, то и всякая функция от r явно также представляет собой инвариант того же преобразования. Если r есть расстояние между двумя точками, то и r + а, r², r³, е^r,... также суть инварианты движения. Какие же особенности отличают расстояние между двумя точками от других форм того же инварианта? Во-первых, расстояние между двумя точками обращается в нуль в том и только в том случае, если две точки совпадают. Эта особенность называется дизъюнктивностью инварианта: он производит дизъюнкцию, т. е. дает критерий различения точек (две точки совпадают, если расстояние равно нулю; они различны, если расстояние отлично от нуля). Ясно, что этому удовлетворяют лишь определенные формы инварианта. Если r есть расстояние между двумя точками, то инварианты r + 1, е^r этому требованию не удовлетворяют; но функции r², r³ все-таки также дизъюнктивны; дизъюнктивностью, таким образом, не определяется еще форма инварианта. Есть еще одна важная особенность, которую нужно уяснить. Если А, В, С суть три точки на одной прямой (вообще говоря, на одной геодезической линии), и если АС есть наибольшее из трех расстояний АВ, ВС и АС, то АС = АВ+ВС. Это свойство расстояния называется аддитивностью по отношению к прямой (геодезической) линии.

Мы можем теперь резюмировать результат рассуждений, приведенных здесь для выяснения формального значения геометрического движения при строго логическом построении системы геометрии, следующим образом.

Геометрические движения с формальной стороны представляют собою группу геометрических преобразований, при которых две точки имеют инвариант, допускающий дизъюнктивную и аддитивную форму (расстояние между двумя точками); других же инвариантов, не выражающихся через расстояние, не существует. Движения, как мы себе их реально представляем, с точки зрения чисто геометрической, составляют лишь одну из интерпретаций этой группы преобразований.

Эта точка зрения, по существу, была высказана Гельмгольцем в мемуаре «О фактах, лежащих в основании геометрии» в 1863 г. но полное развитие, точную научную постановку она получила в многочисленных трудах по основаниям геометрии известного шведского математика Софуса Ли (см.), являющегося творцом той теории непрерывных групп преобразований, к которым относятся преобразования пространства, как множества точек. Все рассуждения, относящиеся к этому вопросу, были здесь для упрощения приноровлены к плоскости. Совершенно ясно, что по существу они относятся и к трехмерному пространству.

12. Движения в интерпретации евклидовой геометрии, данной Пуанкаре. Теперь мы имеем возможность ответить на вопрос, поставленный в конце главы 9-й. Мы привели там интерпретацию евклидовой геометрии, указанную Пуанкаре, и осталось только выяснить, что представляют собой движения в этой системе.

Мёбиус (см.) еще в средине прошлого столетия установил группу замечательных преобразований на плоскости, которые обладают той особенностью, что они преобразуют все окружности в окружности же. Вообще говоря, геометрическое преобразование изменяет форму кривой; но существуют особенные преобразования, которые не меняют формы тех или иных линий; к числу последних принадлежат и круговые преобразования Мёбиуса. К числу этих преобразований принадлежат, в первую очередь, все движения, не меняющие ни величины, ни формы окружностей; сюда же относятся все подобные преобразования, не меняющие формы окружностей, но изменяющие их размеры; сюда относятся также так называемые преобразования посредством обращения, или посредством  обратных радиусов-векторов. Эти последние преобразования, теорию которых можно найти во многих элементарных руководствах¹⁾, иногда преобразовывают окружности в окружности же, а иногда преобразовывают их в прямые. Но мы уже упоминали при изложении интерпретации Пуанкаре, что на прямые можно смотреть как на окружности бесконечно большого радиуса; и именно при этой точке зрения, т. е. при таком условном приобщении прямых к окружностям, можно утверждать, что круговые преобразования преобразуют все окружности в окружности же.

¹⁾ Очень обстоятельное изложение учения о преобразовании обратными радиусами-векторами можно найти в книге Адлера «Геометрические построения».

Если взять любую точку О на плоскости, то всегда существует группа круговых преобразований, которые эту точку О оставляют без изменения (т. е. относят эту точку, как соответствующую, самой себе). Если мы эти соображения применим к интерпретации Пуанкаре и под точкой О будем разуметь ту точку, которую мы исключили из плоскости при построении этой интерпретации евклидовой геометрии, то группа круговых преобразований, не меняющих точки О, и представляет собой движения в этой геометрии. Мы не станем входить здесь в большие подробности, заметим только, что это приводит к чрезвычайно своеобразной интерпретации евклидовой геометрии, осуществляющей последнюю полностью, без каких бы то ни было изъятий. Так как «прямыми» в этой геометрии служат прямые и окружности проходящие через точку О, то «движения», очевидно, замещают «прямые» линии «прямыми» же, как это обычно имеет место в геометрии.

Мы видим, таким образом, что интерпретация евклидовой геометрии, данная Пуанкаре, имеет в основе своей ту точку зрения на геометрию, которая была установлена Софусом Ли. Развитие этих идей, вернее, удачное их применение, привело германского математика Ф. Клейна (1849—1925, см.) к чрезвычайно замечательной интерпретации гиперболической геометрии, которая окончательно решила вопрос о ее логической правильности. Средствами, которыми для этого воспользовался Клейн, являлись, с одной стороны, проективные преобразования, а с другой стороны — замечательные работы английского математика А. Кели (Cayley, 1821—1895), относящиеся к теории квадратичных форм (с точки зрения алгебраической), или к теории кривых второго порядка (с точки зрения геометрической).

13. Неевклидова геометрия в интерпретации Кели-Клейна. Под проективными преобразованиями евклидова пространства разумеют такие преобразования, которые преобразуют все прямые линии вновь в прямые линии. Вообще говоря, как уже было указано выше, форма кривой при преобразовании изменяется. Но подобно тому, как преобразования Мёбиуса преобразовывают окружности в окружности, существуют преобразования, не меняющие формы прямых линий, т. е. преобразовывающие все прямые в прямые же. Конечно, этим свойством обладают, прежде всего, движения; но о них не приходится говорить в том отношении, что движение преобразовывает все линии в конгруэнтные им линии. Вся суть в том, что помимо движений в евклидовом пространстве существует еще множество других преобразований, которые преобразуют все прямые линии в прямые же. Вот эти-то преобразования, впервые указанные Дезаргом, носят название проективных преобразований, или коллинеаций; учение же о проективных преобразованиях составляет предмет проективной геометрии (см. XIII, 331/32, прил., 50 сл.).

Рис. 22.

Дадим здесь представление о проективном преобразовании, ограничиваясь коллинеациями на плоскости. Пусть Q будет плоскость, О — точка, вне ее лежащая (рис. 22). Выберем произвольно вспомогательную плоскость Q' и точку О', лежащую вне обеих плоскостей. Пусть теперь А будет произвольная точка на плоскости Q; спроектируем ее из центра О на плоскость Q', т. е. соединим точку А с точкой О и прямую О А приведем к пересечению с плоскостью О'; пусть А₀ будет точка пересечения. Теперь точку А₀ спроектируем на плоскость Q из центра О', т. е. проведем прямую ОА₀, которая в пересечении с плоскостью Q даст  требуемую проекцию А'. Таким образом, исходя из точки А на плоскости Q, мы построим на той же плоскости другую точку А’, которую и примем за соответствующую первой. Так как теперь каждой точке А плоскости Q будет отнесена соответствующая точка А' (иногда, правда, бесконечно удаленная), то этим установлено некоторое преобразование плоскости Q. Этого рода преобразование, как легко себе уяснить, относит точкам АВС прямой точки А'В'С другой прямой и представляет собою коллинеацию. Это — одно из простейших проективных преобразований; но из них  составляются все вообще проективные преобразования плоскости.

Не останавливаясь здесь на этом  подробнее, заметим только, что существует бесчисленное множество весьма разнообразных преобразований плоскости, преобразующих прямые в прямые же. Эти преобразования, как уже сказано выше, называют коллинеациями, или проективными преобразованиями. Вся совокупность проективных преобразований плоскости образует группу.

Относительно всей группы проективных преобразований одна, две или три точки инварианта не имеют; но четыре точки, расположенные на одной прямой, имеют замечательный инвариант, именуемый сложным, или ангармоническим отношением этих четырех точек.  Пусть А, В, С, D будут четыре точки, расположенные на одной прямой. АС:ВС есть отношение, в котором точка С делит отрезок АВ; точно так же  AD:BD есть отношение, в котором тот  же отрезок делится точкой D. Частное от деления первого из этих отношений на второе называется ангармоническим отношением этих четырех точек, в этом порядке взятых, и обозначается символом (ABCD). Итак:

Значение ангармонического отношения  четырех коллинеарных точек изменяется с изменением порядка точек. Если, например, ангармоническое отношение (1) обозначим через λ, то

Ангармоническое отношение четырех коллинеарных точек есть инвариант всякого проективного преобразования.

Но именно то обстоятельство, что в группе всех проективных преобразований две точки не имеют инварианта, а таковой имеют только четыре точки, лишает нас возможности положить всю группу проективных преобразований в основу геометрической системы, т. е. лишает нас возможности принять ее за группу движений. Но, как чрезвычайно удачно указал Клейн, эта возможность восстанавливается, если ограничиться целесообразно выбранною частью этой группы.

В своих замечательных работах по квадратичным формам Кели показал, что всякому коническому сечению, или кривой 2-го порядка (см. XIII, 331/32, прил., 15, 21) отвечают проективные преобразования, не меняющие этого конического сечения. Чтобы это хорошо выяснить, ограничимся окружностью. Если в плоскости окружности произведем проективное преобразование, то оно, вообще говоря, преобразует эту окружность в некоторую другую кривую 2-го порядка. Но существуют такие проективные преобразования, которые преобразуют все точки этой окружности в точки, принадлежащие этой же окружности; иными словами, эти проективные преобразования не меняют окружности, как целого. Ясно, что если этой окружности не меняют ни преобразование S, ни преобразование S', то ее не меняет и преобразование SS', из них составленное. Поэтому все проективные преобразования, не меняющие этой окружности, образуют группу; такого рода группу принято называть группой Кели, а окружность (в общем случае — коническое сечение), которую преобразования этой группы не меняют, называют абсолютом этой группы.

Итак, пусть окружность О будет абсолютом группы проективных преобразований ∑. Можно показать, что каждое из этих преобразований либо замещает все внутренние точки круга О внутренними же точками, либо заменяет все внутренние точки внешними, и обратно. Выделим те преобразования, которые не меняют всего круга, т. е. все внутренние точки круга преобразовывают во внутренние же его точки. Ясно, что если этим свойством обладают преобразования S и S', то им обладает и преобразование SS'; иными словами, те преобразования группы ∑, которые не меняют всего круга, также представляют собой группу; обозначим ее через σ, а входящие в ее состав преобразования будем обозначать через s, s', s''. Итак, существует группа проективных преобразований, которые не изменяют данной окружности и преобразовывают точки, внутри ее лежащие, в точки, также лежащие внутри этой окружности.

Эту именно группу проективных преобразований Клейн положил в основу замечательной интерпретации неевклидовой геометрии. В этой интерпретации мы будем под «точками» разуметь те точки плоскости, которые расположены внутри нашего абсолюта. Совокупность этих «точек» (т. е. вся часть плоскости, расположенная внутри круга) составит «двухмерное пространство», или «плоскость», в новом значении этого термина. Всякое преобразование s группы σ мы будем называть «движением» в нашей «плоскости». Фигуру в нашей плоскости мы будем называть «конгруэнтной» фигуре В', если существует «движение», т. е. преобразование группы σ, преобразовывающее фигуру В в В'. Пусть А и В будут две «точки» (рис. 23); продолжив прямую АВ, получим в пересечении с окружностью точки С и D (С со стороны точки В, D со стороны точки А). Под «прямой» АВ будем разуметь ту часть обыкновенной прямой АВ, которая лежит внутри абсолюта, т. е. между точками С и D. Для обитателя этой «плоскости» совершенно не существует точек, лежащих за пределом абсолюта.

Рис. 23.

Теперь заметим, что точки С и D определяются точками А и В, и, следовательно ангармоническое отношение (ABCD) определяется двумя «точками» А и В; иными словами, если нам известны «точки» А и В, то мы можем найти точки С и D и вычислить ангармоническое отношение (ABCD); оно представляет собой число, которое известно, если даны «точки» А и В, которое определяется «точками» А и В. Мы можем, поэтому, обозначить ангармоническое отношение (ABCD) короче — через (АВ), т. е. можем положить (ABCD) = (АВ).

С другой стороны, если некоторое «движение» s совмещает «точки» А и В с «точками» А' и В', то эта коллинеация преобразует «прямую» АВ в «прямую» А'В'. Так как точки абсолюта преобразуются также в точки, принадлежащие абсолюту, то точки С и D преобразуются в точки С' и D'. Вместе с тем, вследствие инвариантности ангармонического отношения

(ABCD) = (А'В’С'D'), или (АВ) = (А'В').

Движения в нашей «плоскости» имеют инвариант (АВ), зависящий от двух точек. Посмотрим, обладает ли этот инвариант свойством дизъюнктивности по отношению к двум точкам и аддитивностью по отношению к прямой линии. Если точка А остается неподвижной, а точка В к ней неограниченно приближается, то оба отношения АС:ВС и AD:BD стремятся к 1, а вместе с тем, в силу основного определения (1), к 1 стремится и значение ангармонического отношения (ABCD). Эго можно выразить так: (АА) = (AACD) = 1.

Итак, когда точка В совпадает с А, то значение инварианта группы (АВ) обращается не в 0, а в 1; требование, которым определяется дизъюнктивность инварианта, не соблюдено. Не лучше обстоит дело и с аддитивностью. Пусть точка М лежит на прямой АВ между точками А и В. Тогда в соответствии с определением:

это соотношение вообще не совпадает с соотношением (АВ) = (AM) + (МВ), которым определяется аддитивность инварианта.

Однако, эти дефекты нетрудно исправить одним приемом. Как было выяснено выше, если (АВ) есть инвариант двух точек, то и всякая другая функция от АВ есть инвариант. В соответствии с этим положим 

взяв логарифм при каком угодно основании, превышающем 1.

Тогда соотношения дают:

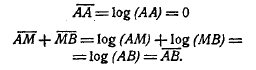
Итак, инвариант , определенный соотношением (2), обладает как дизъюнктивностью по отношению к двум точкам, так и аддитивностью по отношению к трем коллинеарным точкам. Руководствуясь этим, условимся теперь под «расстоянием» между двумя «точками» разуметь число АВ, определяемое соотношением (2). Напомним, что при составлении ангармонического отношения (ABCD) мы условились под С разуметь ту точку абсолюта, которая лежит за точкой В, под D — ту точку, которая лежит за точкой А. Поэтому

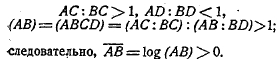
«Расстояние» между двумя «точками» выражается положительным числом. Это число обращается в нуль, когда две «точки» совпадают. Если три «точки» расположены на одной «прямой», то большее из трех расстояний, ими определяемых, равно сумме двух других. Мы находимся в условиях, характеризующих расстояние по воззрениям Гельмгольца и Ли.

Положим теперь, что «точка» А остается на месте, а «точка» В передвигается по прямой АВ к точке С. Когда «точка» В неограниченно приближается к С, то ВС стремится к нулю; поэтому отношение АС:ВС стремится к бесконечности; отношение AD:BD стремится к конечному пределу AD:CD; поэтому ангармоническое отношение (2) стремится к бесконечности, а вместе с тем к бесконечности стремится и его логарифм, т. е. «расстояние» АС. Точки абсолюта, таким образом, являются бесконечно удаленными «точками» нашей «плоскости». Вместе с тем каждый конечый «отрезок» можно продолжить на неограниченное «расстояние».

Таким образом, в нашей плоскости имеют место основные постулаты Евклида, явно и не явно у него выраженные: через каждые две «точки» проходит одна и только одна «прямая»; каждый «прямолинейный отрезок» можно продолжить в обе стороны на «неограниченное расстояние»; от каждой «точки» по каждой «прямой» можно отложить в обе стороны любое «расстояние», а потому вокруг каждой «точки» можно описать «окружность» любым радиусом.

Чтобы отдать себе отчет в том, какова будет геометрия этой «плоскости», остается выяснить вопрос о пятом постулате Евклида.

Рис. 24.

Пусть АВ будет какая-либо «прямая» в нашей «плоскости» (рис. 24), М — «точка», вне ее лежащая. Через нее проведем прямые МС и MD. Легко видеть, что все «прямые» вида MN, проходящие через точку М внутри углов CMD и С'MD', встречают «прямую» АВ; «прямые» же вида МР, проходящие внутри углов DMC' и CMD', «прямой» АВ не встречают (точка встречи этих прямых в обыкновенном значении этого слова лежит за пределами абсолюта, за пределами нашей «плоскости»: «прямой» АВ в этой «плоскости» является только обыкновенный отрезок CD, а потому «прямая» МР «прямой» АВ не встречает). Из сказанного следует, что мы находимся в отношении параллельных линий в условиях геометрии Лобачевского. «Прямые» MD и МС отделяют встречающие прямые от не встречающих; это — две «прямые», выходящие из «точки» М и параллельные «прямой» АВ; они встречают «прямую» АВ в бесконечности, как и должно быть в гиперболической геометрии. Отсюда следует, что интерпретация Клейна осуществляет геометрию Лобачевского на плоскости в полной мере. И действительно, можно шаг за шагом развивать геометрию этой «плоскости», и мы убедимся, что она вполне совпадает с планиметрией Лобачевского. В краткой статье Кели показал, что здесь имеет место тригонометрия гиперболической плоскости. Клейн построил всю гиперболическую геометрию на основе этих идей. При этом он не ограничился плоскостью. Все идеи Кели-Клейна чрезвычайно легко получают распространение на трехмерное пространство. В трехмерном пространстве существует группа коллинеаций, которая имеет инвариантом ангармоническое отношение четырех коллинеарных точек. Выбрав произвольно поверхность второго порядка, лучше всего сферу, можно выделить те проективные преобразования, которые оставляют ее без изменения. Эти преобразования образуют группу, в которой инвариант имеют две точки; этому инварианту можно придать тем же путем дизъюнктивную и аддитивную форму. Остальное выполняется в том же порядке. Таким образом, получается полная интерпретация не только гиперболической планиметрии, но и стереометрии.

Кели и Клейн показали, что существует ряд образов (объектов), по отношению к которым гиперболическая геометрия справедлива вся, без каких бы то ни было исключений, и сомнений в ее логической правильности больше существовать не могло; во всяком случае, такие сомнения могли бы возникнуть относительно геометрии Лобачевского не в большей мере, нежели относительно геометрии Евклида.

14. Идеи Римана. В то время, как Бельтрами, Гельмгольц, Ли, Кели, Клейн дали неевклидовой геометрии направление, которое можно назвать чисто геометрическим, посмертный мемуар Римана (см.) дал им другое направление, которое будет уместно назвать аналитическим.

Мемуар, о котором идет речь, представляет собой пробную лекцию (Habilitations-colloquium), которую Риман прочел в  1854 г. для приобретения звания приват-доцента геттингенского университета. Тема для лекции: «О гипотезах, лежащих в основании геометрии» была избрана Гауссом из числа трех, намеченных Риманом. Это  была лекция, прочитанная Риманом для Гаусса. Этим объясняется чрезвычайная сжатость изложения. На протяжении нескольких страниц намечен ряд чрезвычайно глубоких и совершенно новых идей. Ни вычислений, ни доказательств высказываемых Риманом утверждений мемуар не содержит. Понадобилось много труда, чтобы осуществить эти вычисления и дать, необходимые доказательства. В 1868 г. Дедекинд извлек этот мемуар из наследия Римана и опубликовал его. Идеи Римана трудны не только вследствие сжатого изложения, но и по существу своему. Между тем, именно они приобрели в последнее время исключительное значение не только в геометрии, но и в теоретической физике. Вряд ли было бы поэтому возможным; обойти эти идеи в настоящем очерке; но изложить их в доступном виде не легко; читатель, не владеющий необходимыми для их понимания сведениями из дифференциальной геометрии, может эту главу опустить.

Для того, чтобы определить пространство, необходимо располагать понятием, более общим, из которого понятие пространства можно было бы выделить, указав его особенности, его видовые отличия. Таким более общим понятием, по взгляду Римана, должно служить многообразие, или множество. Этим понятием мы уже пользовались; оно заимствовано Кантором у Римана. Историческая перспектива в настоящем очерке местами принесена в жертву ясности идеи. Риман отличает многообразия  дискретные и непрерывные. В дискретных многообразиях каждый элемент существенно отделен от других; к числу их относится каждое множество, состоящее из конечного числа элементов. В непрерывном многообразии элементы следуют один за другим без промежутков; сюда относятся: линии  поверхности, пространство, как совокупность точек, совокупность цветов; вообще Риман указывает, что число непрерывных многообразий невелико; если речь идет о конкретных множествах, то это, конечно, справедливо.

Положение точки на прямой может быть определено одной координатой, на поверхности — двумя, в пространстве — тремя координатами. Риман выделяет те непрерывные многообразия, в которых элемент может быть задан определенным числом координат, численные значения которых определяются измерением. Многообразие имеет (по определению) n измерений, если его элемент определяется n координатами. Обыкновенное пространство, таким образом, представляет собой многообразие 3 измерений. Если же за элемент многообразия примем определенный момент времени в определенной точке пространства, то для задания этого элемента потребуется четыре координаты: три декартовы координаты, определяющие положение точки в пространстве, и показание часов в рассматриваемый момент. Следуя идее Римана, Минковский (см.) назвал этот элемент мировым моментом. Итак, мировой момент есть определенный момент времени в определенной точке пространства. Совокупность всех мировых моментов составляет многообразие 4-х измерений, которое теперь часто называют миром Минковского.

С точки зрения механистического материализма, все мироздание состоит из вещества, постоянно несущегося во все стороны. В каждый момент в каждой точке находится определенная частица вещества, имеющая определенную скорость. Поэтому, чтобы определить физическое состояние в данный мировой момент (т. е. в данный момент в данной точке), нужно еще определить плотность вещества в этой точке и его скорость; плотность определяется одним числом, а скорость тремя слагающими вектора. Элементом мироздания, рассматриваемого с точки зрения кинематического его состояния, является частица материи, находящаяся в определенный момент в определенной точке и имеющая определенную скорость. Для определения этого элемента необходимо 8 координат (3 координаты точки в пространстве, показание часов, плотность вещества, 3 слагающие скорости). Мироздание в этом понимании представляет собой многообразие 8 измерений.

В обыкновенном пространстве линия определяется тем, что три координаты точки выражаются через один параметр (этим параметром может служить одна из координат, и тогда две координаты выражаются через третью). Поверхность определяется тем, что координаты каждой ее точки выражаются функциями двух параметров. Соответственно этому Риман разумеет под линией в многообразии n измерений совокупность его элементов, которые определяются значениями одного параметра. Если х₁, х₂, х₃,…, х_n суть координаты элемента, то линия в этом многообразии выражается уравнениями:

Каждым значением параметра и при помощи этих уравнений определяется элемент многообразия; совокупность всех этих элементов и образует линию. Линия представляет собой, таким образом, многообразие одного измерения, входящее в состав многообразия n измерений. Таким же образом двухмерной поверхностью в многообразии n измерений называют совокупность элементов, координаты которых выражаются через два параметра:

Совершенно так же определяют поверхности 3- х, 4-х и более высокого числа измерений, входящие в состав многообразия n измерений.

Основным моментом в развитии идей Римана является установление элемента длины. В евклидовом пространстве в ортогональных декартовых координатах элемент длины линии, определяемый точками (х₁, х₂, х₃) и (x₁ + dx₁, х₂ + dx₂, х₃ + dx₃), выражается формулой:

В косоугольных декартовых координатах элемент длины выражается более сложным выражением:

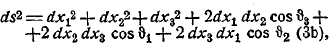
где θ₁, θ₂,  θ₃,   суть углы, попарно образуемые осями координат. В криволинейных, координатах, например, в сферических, кругово циллиндрических, эллиптических и других — элемент длины имеет более сложное выражение, которое, однако, всегда имеет вид:

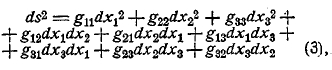
где коэффициенты g_ij суть функции от координат x₁, х₂, х₃ точки, из которой линейный элемент исходит. (Член, содержащий произведение dx₁ dx₂, здесь для симметрии и удобства многих вычислений разбит на два члена g₁₂ dx₁ dx₂ + g₂₁ dx₂ dx₁; при этом принимается g₁₂=g₂₁, общее значение этих двух коэффициентов, таким образом, представляет собой половину всего коэффициента при произведении дифференциалов dx₁ dx₂). Так, если в полярных координатах x₁ означает радиус-вектор точки, х₂ — ее долготу, а х₃ — ее зенитное расстояние, то

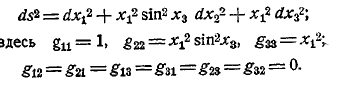
В других координатах эти коэффициенты бывают еще сложнее. Можно сказать, что в трехмерном евклидовом пространстве квадрат элемента длины всегда выражается формулой

где g_ij суть функции от х₁, х₂, х₃, а суммирование распространяется на все значения каждого индекса от 1 до 3.

Сообразуясь с этим, Риман определяет элемент длины в любом многообразии выражением (4), где коэффициенты g_ij суть функции от координат x₁, х₂, х₃,… , х_n, а суммирование распространяется на все значения индексов і и j от 1 до n. Какими же функциями должны выражаться коэффициенты g_ij? Какими угодно; выбрав эти функции, мы устанавливаем геометрию многообразия. Сообразно этому Риман называл всякое многообразие n измерений, в котором установлено выражение элемента длины в форме (4), пространством n измерений. Элементы этого многообразия называются точками пространства. Правая часть равенства (3) представляет собой однородное выражение 2-го порядка относительно дифференциалов dx₁, dx₂,..., dx_n или, как принято говорить, квадратичную форму от дифференциалов. Отличают формы двоякого рода: определенные, которые при всех значениях переменных сохраняют один и тот же знак, и неопределенные, которые могут принимать как положительные, так и отрицательные значения. Так как форма (4) выражает квадрат элемента длины, то Риман, естественно, требует, чтобы это была определенная положительная форма.

В какой же мере геометрия пространства действительно определяется элементом длины? Нижеследующие соображения дадут об этом представление.

Положим, что в пространстве n измерений, определяемом элементом длины (4), задана кривая, выражаемая уравнениями (1). Тогда для элемента этой кривой, выходящего из точки и,

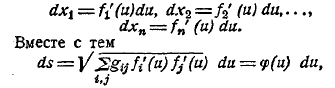
где φ(u) — известная нам функция от u, коль скоро заданы уравнения (1), определяющие кривую. Сообразно этому длина дуги  этой кривой, которая содержится между  точками, определяемыми значениями параметра u₀ и u₁ выражается интегралом

Мы имеем, таким образом, возможность измерять длины любой дуги.

Положим, что через точку М в некотором пространстве проходят две линии. Пусть дифференциалы dx₁, dx₂,..., dx_n определяют выходящий из точки М элемент одной из этих линий, а δx₁, δx₂,..., δx_n — элемент другой; пусть ds будет длина первого элемента, δs — длина второго элемента. Если дело происходит в трехмерном евклидовом пространстве при ортогональных декартовых координатах, то угол между этими элементами, как известно, определяется формулой

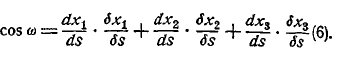
При косоугольных декартовых координатах, каждый элемент дуги выражается формулой (Зb), тот же угол выражается соотношением:

Сличая эти выражения с выражением квадрата линейного элемента, мы видим, что и в том и в другом случае

Нетрудно показать, что при любом выражении элемента длины правая часть выражения (7) представляет собою правильную дробь. Таким образом, в каком угодно пространстве соотношение (7) определяет один, и только один, угол ω (между 0 и π), ему удовлетворяющий; этот угол и принимается за угол между соответствующими линейными элементами, из этой точки выходящими. Положения Римана, таким образом, устанавливают средства измерения не только длин, но и углов.

Как бы ни был выражен линейный элемент (при некоторых оговорках, относящихся к аналитическому характеру функций g_ij), между двумя точками проходит линия, вдоль которой интеграл (5) достигает минимума, т. е. которая имеет между этими точками минимальную длину. Это геодезические линии пространства, которые разыскиваются методами вариационного исчисления (см. XXII, 331/32, прил.). Из каждой точки проходит геодезическая линия в любом направлении.

Плоскость в обыкновенном евклидовом пространстве характеризуется тем, что всякая прямая, имеющая с ней две общие точки, расположена в ней целиком. Аналогичных поверхностей в любом пространстве, т. е. определяемом любым выражением элемента длины, вообще говоря, не существует. Но через любую точку М такого пространства всегда можно провести двухмерную поверхность, которая обладает этим свойством по отношению к точке М в ее окрестности. Это нужно понимать следующим образом.

Если мы точку М обведем на этой поверхности замкнутым контуром достаточно малых размеров и возьмем произвольную точку М₁ внутри этого контура, то геодезическая линия, идущая от точки М к точке М₁, расположена в этой поверхности целиком. Такого рода двухмерная поверхность называется геодезической в точке М. Замечательно, что геодезическая поверхность в данной точке вполне определяется двумя геодезическими линиями, из этой точки выходящими.

Положим теперь, что мы имеем произвольное пространство; выберем в нем произвольно же точку М. Из этой точки проведем два любых линейных элемента.  В направлениях этих элементов проходят две геодезические линии, а двумя геодезическими линиями определяется геодезическая поверхность в этой точке. Следовательно, в каждой точке геодезическая поверхность определяется двумя линейными элементами, из нее выходящими. Если обведем на этой поверхности точку М замкнутым контуром, то получим геодезическую площадку, окружающую точку М и определяемую теми же двумя линейными элементами. Такие площадки можно, следовательно, провести через любые два линейных элемента, подобно тому, как в обыкновенном пространстве через любые два линейных элемента, выходящих из общей точки, можно провести плоский кружок любым малым радиусом. Итак, в произвольном пространстве, из любой его точки, проведем два линейных элемента, а через них проведем геодезическую площадку. Эта геодезическая площадка есть двухмерная поверхность, а потому имеет в точке М определенную кривизну. Эту кривизну Риман называет кривизной пространства в точке М в этой площадке, ее окружающей.

Таким образом, Риманом обобщено учение Гаусса о кривизне поверхности. Поверхность, как ее понимал Гаусс, есть двухмерное пространство: оно имеет в каждой точке определенную кривизну. В пространстве большего числа измерений нельзя говорить о кривизне его в данной точке; можно говорить только о его кривизне в определенной геодезической площадке, окружающей данную точку; в той же самой точке в площадках, различно ориентированных, кривизна бывает, вообще говоря, различная. Кривизна получает определенное значение, когда задана точка М и два линейных элемента (два направления), из нее выходящие и определяющие геодезическую площадку, к которой эта кривизна относится.

Движения в пространстве, как его понимает Риман, суть геометрические его преобразования, образующие группу и сохраняющие без изменения численное значение каждого элемента длины. Если в некоторой площадке существует движение, совмещающее точку М и окружающую ее геодезическую площадку В, в которой кривизна равна К, с точкой М' и площадкой В', в которой кривизна есть К', то К=К'; это есть опять-таки развитие теоремы Гаусса (см. глава 8, ст. 359'/60').

Положим, что в некотором пространстве возможны свободные движения, приводящие любую точку М в любую другую точку М' ив одной и той же точке приводящие путем вращения любую геодезическую площадку в совмещение с любой другой площадкой. Если путем вращения вокруг точки М можно всякую площадку В совместить с любой другой площадкой, то кривизна пространства в каждой точке не зависит от направления площадки; пространство имеет в каждой точке определенную кривизну К. Выражаясь фигурально, можно сказать, что пространство в каждой точке однородно. Если, сверх того, каждую точку М можно привести в совмещение с любой другой точкой М', то кривизна не меняется также от точки к точке. Выражаясь образно, можно сказать, что пространство сплошь однородно во всех своих частях; выражаясь же точно геометрически, нужно сказать, что пространство имеет постоянную кривизну (т. е. кривизну, не зависящую ни от направления площадки в данной точке, ни от положения самой точки).

В евклидовом пространстве трех измерений элемент длины может быть выражен  формулой (За), так как здесь

g₁₁=g₂₂=g₃₃=1, g₁₂=g₂₃=g₃₁=0;

с другой стороны, в выражении римановой кривизны каждый член содержит в качестве множителя производную 1-го и 2-го порядка (по независимым переменным х₁, х₂, х₃) от того или иного коэффициента. Так как здесь эти коэффициенты имеют постоянные значения, то все производные равны нулю, и кривизна евклидова пространства равна нулю во всякой точке и во всякой геодезической площадке, эту точку окружающей. Евклидово пространство трех измерений есть пространство постоянной (нулевой) кривизны.

Имея выражение элемента длины в трехмерном пространстве Лобачевского, или, как говорят теперь, в трехмерном гиперболическом пространстве, Риман вычислил здесь кривизну и обнаружил, что оно имеет постоянную отрицательную кривизну.

У Римана, естественно, возник вопрос о том, нельзя ли построить пространство с постоянной положительной кривизной. Риман обнаружил, что это возможно, и это привело к новой геометрии — римановой в узком смысле слова. Риманова геометрия есть геометрия пространства постоянной положительной кривизны. Эта геометрия чрезвычайно своеобразна. Здесь все геодезические линии — замкнутые конечные кривые; риманово пространство имеет, таким образом, конечные размеры. Параллельных линий здесь не существует: всякие две геодезические линии пересекаются и притом в двух точках. Образцом риманова пространства двух измерений служит сфера. Клейн построил в евклидовом пространстве интерпретацию трехмерного риманова пространства, руководясь теми же идеями Кели, которые его привели к интерпретации гиперболического пространства.

Следуя идеям Римана, Бельтрами показал, как можно построить пространство постоянной кривизны любого числа измерений. Ограничимся только замечанием, что во всяком пространстве постоянной кривизны n измерений элемент длины может быть приведен к виду

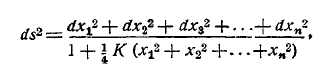
где К есть кривизна пространства. При К = 0 мы получаем обычное выражение элемента длины в евклидовом пространстве; при К > 0 это есть выражение квадрата элемента длины в эллиптическом пространстве, при К < 0 — в гиперболическом.

Пространство четырех измерений в настоящее время приобрело большое значение в теоретической физике. С точки зрения Эйнштейна, для описания соотношений между реальными предметами на всем протяжении мироздания наиболее целесообразным является пользоваться римановой геометрией (см. теория относительности, 423/24. сл.).

15. Обоснование геометрии. Возвратимся теперь к тому вопросу, который послужил источником всего этого ряда новых и своеобразных идей, т. е. к вопросу о пятом постулате Евклида. Какой вывод можно сделать относительно этого постулата из того обстоятельства, что геометрия Лобачевского оказалось логически правильной? Если бы пятый постулат представлял собой следствие из остальных постулатов Евклида, то противоположное допущение как мы уже не раз указывали, неизбежно приводило бы к абсурду. Раз такого абсурда мы не получаем, то это означает, что с остальными постулатами Евклида одинаково совместимы как пятый постулат, так и противоположное положение. Пятый постулат не представляет собой логического следствия из остальных основных положений Евклида и доказан быть не может. Это выражают в настоящее время так: пятый постулат Евклида представляет собой положение, не зависящее от остальных его основных положений. Он неизбежно должен быть внесен в число основных положений или должен быть заменен равносильным ему постулатом, коль скоро мы желаем синтетически построить евклидову геометрию.

Вопрос о пробеле в теории параллельных линий, таким образом, совершенно исчерпан. Но, конечно, в оценке значения идей, к которым привела неевклидова геометрия, это только первый шаг. Идеи эти устанавливают, как вообще должно быть выполнено логическое обоснование геометрии. Самым существенным результатом всех изложенных выше рассуждений является сознание, что геометрические понятия, (термины) не связаны неразрывно с теми наглядными представлениями, которые мы привычно и традиционно с ними соединяем. Напротив, геометрические истины суть формальные суждения, которые могут получать осуществление на весьма разнообразных объектах. Поэтому, формально-логическое построение системы геометрии может действительно удовлетворять требованиям дедуктивной логики только в том случае, если основные понятия будут так определены, чтобы они совершенно не были связаны с какими бы то ни было реальными представлениями. Это должны быть термины, под которые могут быть подведены разнообразные объекты. Вне этого условия нет и не может быть речи о действительно логическом, о формально-дедуктивном построении геометрии. Однако, всякая дедуктивная дисциплина необходимо имеет точки отправления, так называемые основные понятия, определению уже не подлежащие. Каковы должны быть основные понятия при формальном построении геометрии? Ответ на это только один: при строго дедуктивном обосновании геометрии точкой отправления должны служить такие понятия, которые лежат за пределами геометрии, как, например: предметы, или объекты, совокупности, сопряжения и т. п. Этими понятиями мы пользуемся не только в геометрии, но и во всякой другой дисциплине. Всякие действительно геометрические понятия должны быть определены.

Итак, при помощи понятий, так сказать, загеометрических (т. е. вне пределов геометрии лежащих) должны быть определены основные понятия геометрии: точки, углы, линии, поверхности, движения. Эти понятия должны быть связаны основными положениями — постулатами или аксиомами. Постулаты должны быть логически совместны, но независимы между собой. Это значит, что ни один из постулатов не должен противоречить другим и не должен представлять собой следствие остальных. То и другое, т. е. логическая совместность и логическая независимость, должны быть доказаны. Чтобы доказать логическую совместность основных положений, необходимо показать, что существует такая интерпретация, или такое осуществление системы постулатов, при которой все они оказываются справедливыми. В самом деле, если существует такая система объектов, на которой оправдываются все основные положения, то противоречия между ними нет. Далее, чтобы доказать логическую независимость одного постулата от остальных, нужно дать такую интерпретацию всей системы, при которой все остальные положения (т. е. все постулаты, кроме того, независимость которого мы доказываем) осуществлены, этот же постулат несправедлив. Таким образом, если система содержит, скажем, 7 постулатов, то нужно дать 8 интерпретаций, из которых одна должна удовлетворять всем «требованиям» (постулатам), каждая же из остальных должна удовлетворять 6 требованиям, а 7-му не удовлетворять.

Первая строго формальная система геометрии была предложена германским математиком Д. Гильбертом (Hilbert, родился 1862) в 1899 г. в юбилейном сборнике, выпущенном по поводу открытия памятника Гауссу и Веберу в Геттингене. Она обладает чрезвычайно высокими достоинствами, хотя в отдельных своих пунктах и встретила серьезные возражения, потребовавшие исправления некоторых постулатов. Система Гильберта довольно сложна, и изложение ее здесь потребовало бы много новых разъяснений. Чтобы дать понятие о построении формальной геометрической системы в порядке выраженных выше идей, мы изложим здесь систему, предложенную автором настоящей статьи в 1905 г. в сочинении «Основания геометрии».

16. Система евклидовой геометрии. Положим, что мы имеем какое-либо множество, или многообразие, элементами которого могут быть какие угодно объекты. В этом многообразии установим различные сопряжения его с самим собою; как мы видели выше, это всегда возможно сделать в любом многообразии. Сопряжения эти могут быть какие угодно; мы даже не предполагаем, что это должны быть непременно совершенные сопряжения. Далее, каждой паре различных элементов этого многообразия отнесем произвольно выбранное арифметическое число, отличное от нуля; это также, конечно, можно выполнить разнообразнейшими способами.

Таким образом, мы будем иметь многообразие, в котором установлена некоторая система сопряжений его элементов и каждой паре элементов соответствует некоторое арифметическое число произвольно, по нашему усмотрению, ей отнесенное. Когда этот процесс выполнен (т. е. когда установлены сопряжения и арифметические числа, отнесенные каждой паре элементов), мы будем называть многообразие геометрическим пространством, его элементы — точками, установленные в нем сопряжения — движениями, а числа, отнесенные парам точек, расстояниями между точками. Так как эти сопряжения (движения) можно устанавливать чрезвычайно разнообразно и разнообразно же можно распределять между точками расстояния, то чрезвычайно разнообразны могут быть пространства. Соотношения, проистекающие из характера установленных в пространстве движений и расстояний, и составляют геометрию этого пространства.

Два пространства могут отличаться многообразиями, служащими для каждого из них субстратом; при выбранном многообразии они могут отличаться царящими в них движениями; при тех же движениях они могут различаться расстояниями между точками.

Пусть А, В, С будут три точки некоторого пространства; им соответствуют три расстояния АВ, ВС, АС, положим, что АС есть большее из этих трех чисел. Может случиться, что АС = АВ + ВС; в таком случае мы будем говорить, что точки А, В и С расположены прямолинейно и точка В лежит между точками А и С.

Так как распределение расстояний между точками может быть сделано совершенно произвольно (при самом построении пространства), то возможны пространства, в которых прямолинейное расположение трех точек вовсе не имеет места. Существуют пространства, в которых между одними точками имеются промежуточные точки, а между другими их нет. Существуют пространства, в которых между двумя точками на определенных от них расстояниях есть промежуточные точки, а на других расстояниях — нет. Наконец, существуют пространства, в которых между любыми двумя точками А и В существует промежуточная точка. В соответствии с этим мы можем условиться сделать предметом своего исследования только такие пространства, в которых выполняется следующее требование (постулат):

Постулат I. Между любыми двумя точками А и В, на любом расстоянии, меньшем АВ, от любой из них, имеется промежуточная точка.

Этим постулатом из числа всех возможных пространств выделена очень обширная группа. Подчиняя пространства этой группы новым требованиям, мы будем их все более и более специфицировать, отпечатлевая их особенности. Совокупность точек, обладающих тем свойством, что любые три из них расположены прямолинейно, мы будем называть прямолинейным образом. Пусть А и В будут две точки некоторого пространства, удовлетворяющего первому постулату. Положим, что каждая из точек С и D расположена прямолинейно относительно точек А и В. Образуют ли четыре точки А, В, С и D прямолинейный образ? Иными словами, влечет ли то обстоятельство, что точки С и D расположены прямолинейно относительно точек А и В, также прямолинейное расположение точки А относительно С и D и точки В относительно С и D? Исследование обнаруживает, что иногда это имеет место, иногда нет. Мы можем ограничиться изучением тех пространств, в которых это имеет место, и соответственно этому поставить следующее требование:

Постулат II. Если точки С и D расположены прямолинейно относительно точек А и В, то и обратно, точки А и В расположены прямолинейно относительно точек С и D.

В пространстве, удовлетворяющем этим двум постулатам, мы будем называть прямой АВ образ, состоящий из двух точек А и В и всех тех точек пространства, которые расположены прямолинейно относительно А и В. Основываясь на приведенных двух постулатах, можно доказать, что прямая представляет собою прямолинейный образ и вполне определяется любыми двумя своими точками.

Совокупность точек прямой АВ, лежащих между точками А и В, образует вместе с точками А и В отрезок АВ. В тесной связи с этим находится и следующая терминология. Если точка О на прямой АВ лежит между точками А и В, то говорят, что точки А и В лежат по разные стороны от точки О; если точка О прямой АВ не принадлежит отрезку АВ, то говорят, что точки А и В лежат по одну сторону от точки О. Эти понятия вводят нас в учение о расположении точек на прямой. Следующие четыре теоремы составляют основу этого учения.

1) Если три точки А, В и С расположены прямолинейно и точка В лежит при этом между А и С, то четвертая точка D не может лежать одновременно между А и В и между В и С.

2) Если точки А, В и С расположены прямолинейно и точка В лежит между А и С, а четвертая точка D расположена между А и В, то точка В лежит между D и С.

3) Если три точки А, В и С расположены прямолинейно, причем В лежит, между А и С, а четвертая точка D лежит между А и В, то точка D лежит, между точками А и С.

4) Если четыре точки А, В, С и D образуют прямолинейный образ и при этом как точка В, так и точка D расположены между А и С, то точка D лежит либо между А и В, либо между В и С.

Опираясь на эти теоремы можно доказать предложение, составляющее наиболее существенную часть учения о расположении точек на прямой. Оно заключается в следующем. Если О есть некоторая точка прямой линии, то все остальные точки на этой прямой распадаются на две категории, обладающие следующими свойствами: если А и В суть точка одной и той же категории, то они расположены по одну сторону от точки О; если же точка А принадлежит одной категории, а точка В принадлежит другой, то точки А и В расположены по разные стороны от точки О. Эти две категории точек образуют две стороны прямой относительно точки О или две стороны, на которые точка О делит прямую. Мы приходим, таким образом, к формальному обоснованию важного понятия, которым мы обыкновенно владеем исключительно интуитивно.

Теперь обратимся к движениям. По определению, это суть какие угодно сопряжения пространства с самим собою. Ввиду этого возможны пространства, в которых при совмещении точек А и В с точками А' и В' расстояния АВ и А'В' могут не быть равны между собой; в других пространствах при этих условиях АВ=А'В'. Мы можем выделить эти последние пространства. Это приводит к следующему постулату:

Постулат III. Если некоторое движете совмещает точки А и В с точками А' и В', то расстояния АВ и А'В' равны.

Этот постулат устанавливает, что расстояние между двумя точками при движении остается инвариантным.

Сопряжения, представляющие собой движения в нашем пространстве, ничем ближайшим образом не охарактеризованы; это могут быть даже несовершенные сопряжения. Четвертый постулат устраняет эту возможность.

Постулат IV. Никакое движение не приводит двух различных точек пространства в совмещение с одной и той же точкой.

Пятый постулат устанавливает, что движения образуют группу.

Постулат V. Каковы бы ни были движения S и S' в пространстве, существует движение SS', заменяющее последовательное производство их.

Содержание постулатов III-V можно выразить коротко и совместно так: движения представляют собой группу совершенных преобразований, для которых расстояния представляют собой инварианты. Таким образом, эти постулаты являются выражением точки зрения С. Ли на сущность движений.

Если некоторое движение оставляет какую-либо точку в покое (т. е. сопрягает ее с самой собой, относит ее к самой себе в качестве соответствующей, еще иначе — преобразовывает ее в самое себя), то оно называется вращением вокруг этой точки. Если движение оставляет в покое несколько точек или какой-либо образ, то оно называется вращением вокруг этих точек или вокруг этого образа.

Положим, что в некотором пространстве вращение вокруг двух точек А и В приводит точку С в совмещение с точкой С'. В таком случае в силу постулата III:

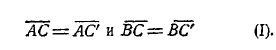
Положим теперь, обратно, что имеют место соотношения (I). Всегда ли при этих условиях в пространстве существует вращение вокруг точек А и B, совмещающее точку С с точкой С'? Исследование обнаруживает, что существуют пространства, удовлетворяющие установленным уже пяти постулатам, но этому требованию не удовлетворяющие; существуют также пространства, в которых это требование удовлетворено. Сообразно этому мы можем установить следующий постулат:

Постулат VI. Если точки С и С' одинаково удалены как от точки А, так и от точки В, т. е., если имеют место соотношения (I), то существует вращение вокруг точек А и В, приводящее точку С в точку С'.

Пользуясь всеми этими постулатами, можно легко установить, что движение, оставляющее две точки в покое, оставляет в покое и прямую, их соединяющую. Но если движение оставляет в покое три точки, не лежащие на одной прямой, смещает ли оно другие точки? В некоторых пространствах такое смещение происходит, а в других оно не имеет места. Сообразно этому мы можем установить следующий постулат:

Постулат VII. Если некоторое движение оставляет в покое 3 точки, не лежащие на одной прямой, то оно оставляет в покое все точки пространства.

Остающиеся постулаты связаны с понятием о плоскости. В этой системе разработки геометрии понятие о плоскости связывается с геометрическим местом точек, одинаково удаленных от двух данных точек. В некоторых пространствах этим геометрическим местом служит только одна точка (середина отрезка, соединяющего эти точки); в других пространствах этим геометрическим местом служит прямая (например, если это есть двухмерное евклидово пространство); наконец, существуют пространства, в которых это геометрическое место имеет также точки, не расположенные на одной прямой. Если геометрическое место точек, равно удаленных от двух точек, содержит точки, не расположенные на одной прямой, то мы будем называть его плоскостью. Вместе с тем мы можем установить следующий постулат:

Постулат VIII. В пространстве существует плоскость.

Положим, что точки А и В лежат вне плоскости Р. Если отрезок АВ не встречает плоскости, то говорят, что точки А и В расположены по одну сторону от плоскости; если отрезок АВ встречает плоскость, то говорят, что точки расположены по разные стороны от плоскости. Пусть А, В, С будут три точки, не принадлежащие плоскости, при чем точки А и В и точки В и С расположены по одну сторону от плоскости. Будут ли точки А и С также расположены по одну сторону от нее? В противность всей нашей интуиции бывают пространства, в которых это не имеет места. Мы можем поэтому установить постулат:

Постулат IX. Если точки А и В, а также точки В и С расположены по одну сторону некоторой от плоскости, то точки А и С также расположены по одну сторону от той же плоскости.

Эти 9 постулатов оставляют выбор только между геометрией Евклида и геометрией Лобачевского. Поэтому, присоединяя в качестве десятого постулат Евклида, мы получаем систему основных положений, вполне определяющих евклидово пространство. Конечно, чтобы вполне отчетливо себе уяснить систему геометрии, в этом порядке идей построенную, необходимо проделать доказательства важнейших теорем. Система, во всяком случае, дает формальное обоснование геометрии.

В качестве недостатка этой системы в литературе указывали, что она вводит в геометрию с первых же шагов число. Между тем геометрию надлежит развивать чисто геометрическими средствами, не прибегая к арифметике: geometriam geometrice. Однако, метрическую часть геометрии, т. е. учение об измерении длин, площадей и объемов, невозможно строить, не пользуясь арифметикой. Вопрос, таким образом, только в том, с какого момента обращаться к арифметическим средствам. Всю геометрию положения действительно можно построить, не прибегая к арифметическим средствам; для этого необходимо четыре теоремы о расположении точек на прямой, выше здесь приведенные, ввести в качестве  постулатов. Так Гильберт и поступает. В его системе постулаты распадаются на 5 групп. Первую образуют постулаты связи: две точки определяют прямую; — три точки, не лежащие на одной прямой, определяют плоскость; — если две точки лежат на плоскости, то и прямая, ими определяемая, целиком лежит в той же плоскости; в системе Гильберта все эти предложения представляют собою постулаты. Вторую группу образуют постулаты, относящиеся к расположению точек на прямой; по существу они мало отличаются от приведенных выше четырех предложений. Третью группу образуют постулаты, относящиеся к движению. Четвертую группу образуют аксиомы о непрерывности; к этим идеям мы еще возвратимся ниже. Наконец, пятую группу составляет постулат Евклида, который Гильберт, впрочем, вводит раньше.

После всех этих исследований было опубликовано еще немало работ, упрощающих геометрическую систему, устанавливающих логические посылки проективной геометрии, эллиптической или гиперболической геометрии и т. д. Но по существу задача о формальном построении геометрии разрешена.

17. Гносеологический подход к теоретическим основам геометрии. Все рассуждения, которыми мы занимались выше, имели источник методологический. Самая задача ставилась как определенный метод построения системы геометрии; все внимание было сосредоточено на тех перипетиях научной мысли, которые прямо или косвенно вели к разрешению этой задачи. Но в самой тесной связи с этой проблемой стоит другой вопрос — об источнике математического познания вообще, геометрического в частности. Откуда почерпнуты, каким путем добыты наши представления о пространстве, соотношения между пространственными образами и те геометрические предложения, которые служат выражением пространственных соотношений? Геометрия разматывается дедуктивными средствами из небольшого числа посылок. Но каким образом установлены или приобретены эти посылки? Вряд ли будет преувеличено, если мы скажем, что интересы гносеологии (науки об источниках нашего познания, см. теория познания) были более всего сосредоточены на этом именно вопросе. Он занимал умы философов уже в глубокой древности; он часто служит предметом ожесточенного спора в наши дни. Аристотель в заключительной главе «Второй Аналитики» классифицирует различные точки зрения на этот вопрос, по существу, так же, как это через два с лишком тысячелетия сделал Гельмгольц. В своей «Физиологической Оптике» Гельмгольц определенно формулирует две точки зрения на этот предмет, которые характеризуют два основных взгляда, по отношению к этому вопросу сложившиеся. Одни считают, что источник наших геометрических познаний коренится в тех свойствах нашего духа, которые мы несем с собой от рождения; философов, отстаивающих эту точку зрения, Гельмгольц называет нативистами. Другие признают наблюдение и опыт единственным источником познания, а потому считают, что и геометрические наши познания мы черпаем из того же кладезя; этих философов Гельмгольц называет эмпиристами. В эпоху Гельмгольца уже нельзя было ограничиться общей схемой, и потому он эту характеристику углубляет. Нативисты усматривают источник наших пространственных представлений в нашей организации, в самом устройстве нервной системы, органа зрения, органа осязания. Они считают, что способом восприятия впечатлений, который обусловливается устройством органов восприятия, определяется и то, как мы относим эти восприятия во внешний мир, как мы их локализируем во времени и в пространстве. Устройством глаза и зрительных центров определяется не только то, как мы воспринимаем впечатления, производимые телами на орган зрения, но и то, как мы эти впечатления, так сказать, проецируем вовне. Напротив, эмпиристы приписывают в процессе приобретения пространственных представлений преимущественное значение упражнению, сознательному и бессознательному опыту, часто связанному с волевыми побуждениями и вообще с психологическими мотивами. Сам Гельмгольц причисляет себя к наиболее устойчивым эмпиристам, хотя в проведении эмпирической точки зрения он, несомненно, не проявляет той совершенно непоколебимой твердости, которая так ярко выражена у Дж. Ст. Милля. Наиболее яркими представителями нативистов в XIX ст. являются У. Джемс, И. Миллер и особенно Э. Геринг, хотя все они проводят нативистское учение весьма различно. Однако, Вундт считает, что не всякое психологическое воззрение, противопоставляемое нативизму, может быть признано эмпиризмом. Он предпочитает поэтому подразделить воззрения по этому вопросу на нативистское и генетическое, генетическое же воззрение он подразделяет на эмпирическое, как оно было охарактеризовано .выше, и ассоциативное, которое все-таки видит основу образования пространственных представлений не только в воздействии внешнего мира, в опыте и упражнении, но и в ассоциациях, в сближениях воспринятых ощущений, которые являются продуктом нашей душевной деятельности и в известной мере предшествуют опыту. Но наиболее трудно в этой классификации отвести место воззрениям Канта, игравшим в истории этого вопроса совершенно исключительную роль.

Сущность взглядов Канта заключается в следующем. Акт познавания, несомненно, всегда начинается с опыта, с внешних чувственных восприятий. Но когда это восприятие осуществляется, воспринимаемые ощущения, достигая нашего сознания,  налагаются на определенную его структуру, на определенные, уже готовые формы сознания, существующие до всякого опыта. Вне этих форм никакое познание невозможно. Эти формы Кант называет познанием а priori. Совокупность априорных знаний составляет достояние чистого разума. Учение о деятельности разума, когда он оперирует исключительно априорными знаниями, должно составить теорию чистого разума. Кант не считает еще возможным создать такую теорию; он пишет только пропедевтику к ней или «критику чистого разума», имеющую целью отделить то, что  ему не принадлежит, и этим путем выяснить его действительное достояние — познание а priori. Две черты, по взглядам Канта, характеризуют априорное знание: во-первых, его аподиктичность и, во-вторых, — всеобщность, не знающая исключений (см. XXIII, 339 сл.). Такие априорные истины, по мнению Канта, присущи каждой науке; но в математике они доминируют. Математика вообще, и геометрия в частности, вся разматывается из некоторого числа априорных, присущих нашему разуму положений. Все основные свойства пространства, т. е. все основные положения геометрии составляют априорное достояние нашего разума. Для их утверждения не может быть места никакому опыту, ибо они вполне аподиктичны. Если, например, некоторый опыт говорил бы против того положения, что через две точки можно провести только одну прямую, то мы с полной уверенностью сказали бы, что неправильность лежит в опыте, а не в этом основном положении: мы были бы уверены, что ошибка лежит в осуществлении опыта, а при таких условиях опыт не может играть никакой роли в обосновании истины. Все, что добывалось путем опыта, всегда было чревато сомнениями, отступлениями, исключениями; многое требовало исправления, многое оказывалось даже ложным. Математика ничего подобного не знает. Ее истины всегда были незыблемы и не вызывали сомнений в течение тысячелетий. Причина этого — их априорность. Учение об априорности отнюдь не совпадает с нативизмом. Здесь дело не в физической конструкции наших органов восприятия, не в прирожденных агентах, определенным образом физиологически преломляющих воспринимаемые нами ощущения. Здесь существо дела, по взглядам Канта, в определенных формах сознания, присущих нашему духу, в известном смысле составляющих существо этого сознания.

Милль в «Системе логики» подробно останавливается на вопросе о происхождении геометрических аксиом. Будучи решительным эмпиристом, он противополагает взглядам Канта следующие соображения. Бывают опыты, так сказать, нарочитые, с определенной целью производимые, — будем их называть экспериментами, — и опыты, осуществляемые попутно в нашей житейской практике, в нашей повседневной деятельности; этого рода опыты будем называть «эмпирическими переживаниями». Эксперименты, специально производимые для проверки того или иного научного положения, необходимо бывают редки, носят единичный характер даже в том случае, если они проверяются целым рядом ученых. В этом, так сказать, спорадическом характере эксперимента, мало разнообразного и часто одностороннего, коренятся источник его недостаточной надежности. Но эмпирические переживания носят массовый характер; если они систематически приводят к одному и тому же результату, то они глубоко внедряют устанавливаемую ими истину в наше сознание. Эмпирические переживания, относящиеся к первоосновам геометрии, сопутствуют почти каждому нашему движению. Они испытываются всеми, кто сознательно относится к окружающему миру; они осуществляются массами людей и из года в год, из столетия в столетие дают один и тот же результат. И этим путем в течение тысячелетий эти истины глубоко внедрились в ваше сознание, сделались необходимым достоянием нашего ума. Может быть, теперь ребенок уже несет в себе зародыши этих знаний; но происхождение их все-таки эмпирическое, они представляют собой результат вековых и массовых эмпирических переживаний. (Ср. XXVIII, 639/40).

Как воззрения Канта, так и взгляды Милля встречали решительные возражения. Учение об априорности геометрических истин встречало возражения двоякого рода: одни носили, так сказать, эмпирический, другие — принципиальный характер. Воззрения первого рода заключались в том, что априорные истины должны были бы быть достоянием всякого человека, независимо от уровня его развития; между тем усвоение геометрических истин требует уже значительной интеллигентности и иногда не без труда дается лицам уже подготовленным. Возражения принципиального свойства находились в связи с необычайным взмахом опытных наук в XIX ст. С каждым десятилетием крепло позитивное направление мысли, крепло механистическое мировоззрение, материалистическое понимание всего окружающего. На этой почве априоризм Канта, естественно, отдавал метафизикой, тем более, что Кант на всю критику чистого разума смотрел как на теорию метафизики. И чем шире развертывались успехи эмпирических наук, чем глубже внедрялось материалистическое мировоззрение, тем яснее становился совершенно метафизический характер учения Канта. Были сделаны многочисленные попытки примирить учение Канта с воззрениями эмпиристов; но тенденциозная искусственность этих попыток так ясна, что о них вряд ли даже стоит серьезно говорить. Но и противники Канта не чувствовали под своими учениями той твердой почвы, которая во всех остальных отраслях естествознания крепла с каждым днем и часом. Самые убежденные эмпиристы не могли не чувствовать, что геометрию от чисто эмпирических наук все-таки отделяет целая пропасть. Что в геометрическом познании есть очень глубокий эмпирический элемент, в этом не может быть сомнений. Но совершенно особенная точность геометрии ставит ее в исключительное положение, и рассуждения Милля, несомненно, оставляют чувство неудовлетворенности. Трудность заключается в том, чтобы эту особенную точность разъяснить до конца, найти ее источник, пролить на этот вопрос полный яркий свет. Опыт, ведь, вообще не может дать ничего больше, чем он фактически устанавливает; это, между прочим, составляет основную точку зрения Милля как в теории индукции, так и в учении о силлогизме. Между тем вера в совершенную точность этого рода предложений у нас гораздо глубже, нежели сознание, что опыт их подтверждает; опыт всегда  дает подтверждение этого только с приближением. Более того, геометрические истины всегда относятся к идеальным образам, которые конкретно вообще нельзя воспроизвести. Здесь происходит неизмеримо, более глубокий процесс отвлечения, чем в чисто экспериментальных науках; истолкование этого процесса с его логической и психологической стороны оставалось недоступным. Именно в поисках за источником этих сомнений некоторые философы, пытались примирить учение об априорности с чистым эмпиризмом; Роль и сейчас еще стоит на той точке зрения, что между этими учениями нет глубокой разницы. Мы совершенно убеждены, что попытки примирения этих противоположных учений столь, же безнадежны, как и попытки примирения религии с наукой.

Источник геометрического познания оставался для этих философов неразгаданной загадкой. На помощь пришли геометры и дали своеобразный ответ на этот вопрос.

Первым шагом в этом деле было открытие неевклидовой геометрии, которая является такой же строгой, такой же незыблемой, такой же совершенной математической системой, как и геометрия Евклида. Учение об априорности именно евклидовой геометрии с этим совершенно не вяжется. Как могла бы существовать другая геометрия, если бы евклидова геометрия составляла неотделимую от человека форму его мышления? Это — первый этап на пути новых воззрений. Далее выяснилось, что евклидова же геометрия, как формальная система  не связана непременно с теми представлениями, которые мы с ней соединяем; она  может получать и иные интерпретации. Такие же разнообразные наглядные интерпретации получили и другие геометрические системы. Разница лишь в том, что евклидова система чаще получает применение к окружающим нас предметам. Таким образом, выработалось сознание, что геометрия есть наука чисто формальная. Основные ее положения представляют собой не истины априорного происхождения. (Кант), не научные гипотезы (Риман) или факты, заимствованные из опыта (Гельмгольц, Милль), а формальные, условно устанавливаемые положения (постулаты); принципиально эти постулаты подчинены только одному требованию — они не должны находиться во взаимном логическом противоречии. Фактическая же ценность их заключается в том, что они с большим приближением отображают те соотношения между материальными телами, которые мы называем пространственными. Эти соотношения, с которыми мы постоянно имеем дело, и привели к установлению соглашений — постулатов геометрии. Из этих постулатов геометрия разматывается совершенно дедуктивно. Различным комбинациям постулатов соответствуют различные геометрические системы. Строгость и незыблемость геометрических предложений коренится исключительно в том, что основные положения не содержат логического противоречия. Эту точку зрения с полной отчетливостью в первый раз выразил Г. Гроссман в следующих словах: «Все науки в высшем своем подразделении распадаются на реальные и формальные. Первые отражают в нашем мышлении бытие, являющееся нашему сознанию независимо от него; истинность этих наук покоится на соответствии между этим бытием и нашим мышлением. Вторые имеют своим предметом то, что предложено самой человеческой мыслью, и истинность их заключается во взаимном согласии процессов нашего мышления».

Но, если посылки могут быть выбраны совершенно произвольно, то чем же мы должны руководствоваться, производя выбор этих посылок? Что служило путеводной нитью при избрании посылок, приведших к геометрии Евклида? Эту руководящую роль играл, конечно, опыт. Геометрия есть известная формальная система, служащая, как уже сказано, для выражения тех свойств физических тел, которые, связаны с их протяженностью. Эта система так подобрана, чтобы эти свойства с ее помощью было удобно выражать.

Торговые фирмы часто устанавливают между собой краткие условные знаки для своих сообщений. Чем руководятся они при выборе этих соглашений? Конечно, сознанием того, что им при этих сношениях чаще всего приходится друг другу передавать — опытом. Но этот язык все-таки остается условным, и говорить, что он связан с природой торговли, совершенно лишено смысла. Нечто подобное мы имеем и в математике. Встречая постоянную нужду для выражения известных соотношений между внешними предметами, относящихся к их количеству и размерам, человек постепенно выработал известную схему, с помощью которой он с значительным успехом эти соотношения выражает. Чем тоньше становятся соотношения, которые он должен выражать, тем детальнее и разнообразнее развивается подобранная для этого система. Наше сравнение, конечно, грубое; оно может служить только некоторой иллюстрацией для уяснения глубокого замысла конвенционалистов.

Эта точка зрения, в основе которой лежит соглашение — конвенция, получила наименование конвенционализма. Ее родоначальниками нужно считать Г. Грассмана, Фреге в Германии, Пеано и Пиери в Италии. Мастер слова Пуанкаре выражает эту точку зрения в следующих выражениях: «Многие гипотезы только кажутся таковыми, а в действительности сводятся к определениям и чистым соглашениям. Гипотезы этого рода встречаются особенно часто в математике и в смежных с нею дисциплинах. Именно отсюда и проистекает строгая точность этих наук; эти соглашения представляют собой продукт свободного творчества нашего духа, который в этой области не знает преград. В этой области наша мысль может настойчиво проявить свою силу, ибо здесь она повелевает. Спросим себя, однако, произвольны ли эти повеления или нет? Конечно, нет, ибо иначе они были бы бесплодны. Опыт предоставляет нам свободный выбор посылок, но он нами руководит, помогая нам избрать наиболее удобный путь». Пуанкаре — не выдержанный мыслитель, и воззрения его часто сбивчивы.  Но здесь он точно выражает точку зрения, признанную в настоящее время едва ли не всеми математиками, которые этими вопросами серьезно занимались. Вся математика, несомненно, представляет собой ряд соглашений, подобранных для выражения определенных реальных соотношений; при выборе этих соглашений нами руководит опыт; учение об априорности сделалось достоянием истории.

18. Геометрия и арифметика. Возвратимся теперь к вопросу об основаниях геометрии. Мы выяснили выше, каким образом было обнаружено, что неевклидова геометрия не содержит внутренних противоречий. Как мы видели, это было достигнуто тем, что была найдена интерпретация, в полной мере осуществляющая неевклидову геометрию. Однако, все эти интерпретация представляют собой геометрические комбинации в области евклидовой геометрии. Так, интерпретация, принадлежащая Кели и Клейну, как мы видели, имеет в своем основании совокупность точек, лежащих внутри конического сечения, в простейшем случае — внутри окружности. Иными словами, в клейновой интерпретации двухмерной гиперболической геометрии многообразием, осуществляющим это пространство, служит совокупность точек евклидовой плоскости, расположенной внутри окружности; движениями служат проективные преобразовании   евклидовой плоскости, оставляющие окружность (абсолют) без изменения. Таким образом, интерпретация неевклидовой геометрии осуществляется в пределах евклидова пространства. Доказательная сила всего рассуждения коренится, таким образом, в непреложности евклидовой геометрии. Но, согласно принципам, нами установленным, в основе всякой геометрии должна лежать система посылок (постулатов), не содержащая внутренних противоречий. Откуда же может быть почерпнута уверенность, что посылки, лежащие внутри евклидовой геометрии, не содержат противоречия? Интерпретация посылок, которая должна быть для этой цели создана, уже не может быть заимствована из евклидовой геометрии; иначе мы очутились бы в ложном круге. Но какой же иной материал, который не вызывал бы сомнений, мы имеем для построения такой интеретации евклидовой геометрии?

Мы обратимся для этой цели к аналитической геометрии. Пусть х, у, z будут ортогональные декартовы координаты точки. Квадрат расстояния между двумя точками (х₁, y₁, z₁) и (х₂, y₂, z₂), как известно, выражается формулой:

Теперь посмотрим, как выразятся аналитически движения евклидова пространства. Пусть S будет какое-либо из этих движений. Оно приводит произвольную точку х, у, z в точку х', у', z'; ясно, что координаты х', у', z' должны быть функциями от х, у, z.

Функции эти должны удовлетворять следующим двум условиям: во-первых, уравнения (2) должны выражать совершенное преобразование, т. е. каждой системе значений х,у, z должна от ечать одна и только одна система значений переменных х', у, z', и обратно; во-вторых, они должны представлять коллинеацию, т. е. они должны преобразовывать прямые линии в прямые линии; выражаясь аналитически, они должны преобразовывать линейные уравнения в линейные же уравнения. Этим двум требованиям без каких бы то ни было изъятий уравнения (2) могут удовлетворять только в том случае, когда правые их части представляют собою целые линейные функции. Иными словами, уравнения эти должны иметь вид:

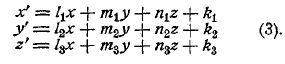
С другой стороны, эти преобразования  должны оставлять инвариантным выражение (1), так как расстояние остается при движении без изменения. Но соотношения (3) дают:

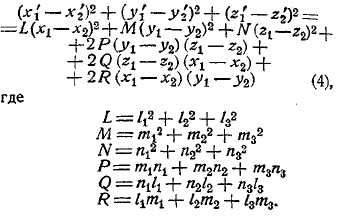
Для того, чтобы правая часть равенства  (4) совпадала с выражением (1) при всех значениях координат, необходимо и достаточно, чтобы:

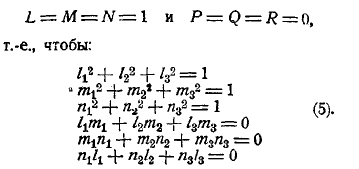
Итак, движения в евклидовом пространстве суть преобразования, которые в ортогональных декартовых координатах выражаются уравнениями (3). В преобразования (3) входит 12 постоянных (параметров), обозначенных буквами I, m, n, k с индексами 1, 2, 3, но эти параметры связаны 6 уравнениями (5), и, следовательно, произвольных параметров остается 6. Это является аналитическим выражением того, что движения в трехмерном евклидовом пространстве имеют 6 степеней свободы.

Сделаем еще один шаг дальше. Числа х, у, z суть координаты точки в евклидовом пространстве. Мы теперь согласимся, что под «точкой» будем разуметь просто совокупность трех чисел х, у, z, или, иначе, совокупность значений трех независимых переменных x, у, z. Выражаясь короче, мы «точкой» будем называть числовой триплет. Совокупность всех возможных «точек», т. е. всевозможных числовых триплетов, составит то многообразие, в котором мы установим геометрию и этим претворим его в «пространство». Это будет достигнуто, если мы установим в этом многообразии движения и расстояния между его «точками». С этой целью согласимся под «расстоянием» между двумя «точками» (x1, у1, z1) и (х₂, у₂, z₂) разуметь число, выражаемое формулой (1). Под «движениями» будем разуметь преобразования числовых триплетов, выраженные уравнениями (3), в которых параметры связаны соотношениями (5). Пространство, в которое мы этим путем превратили наше численное многообразие, обладает геометрией Евклида.

Мы, таким образом, пришли к своеобразным пространствам, в которых «точками» служат комбинации чисел; этого рода пространства называют аналитическими, или арифметическими. Имеющие в них место соотношения устанавливаются арифметическим или алгебраическим путем; они имеют поэтому ту достоверность, какую имеет арифметика и ее развитие — алгебра, анализ. Логическая правильность евклидовой, да и всякой другой геометрии устанавливается арифметикой и анализом; геометрия имеет ту достоверность, какую имеет арифметика. Во всей литературе все доказательства логической совместности постулатов и их независимости всегда без исключения устанавливаются средствами арифметики и анализа. Геометрия удостоверение в логической правильности черпает в арифметике. Учение об основаниях геометрии этим исчерпывается; все вопросы, которые с этим связаны, переносят нас в область арифметики и анализа. Трудно сказать, кто из двух родных сестер — геометрии и арифметики — старше; но в деле своего логического самоопределения геометрия опирается на арифметику.

19. Обоснование арифметики и догматический подход к теоретическому основанию математики. Счет несомненно, предшествовал созданию геометрических понятий. Но значительное развитие арифметика получила гораздо позже, нежели геометрия (см. арифметика). Причина этого коренилась в крайней сложности  систем нумерации, которыми пользовались все древние народы. В непрерывных поисках лучших средств счета, в стремлении справиться с практическими задачами, стоявшими перед арифметикой, в борьбе абацистов и алгорифмиков (см. арифметика, III, 453) вопросы логического обоснования арифметики стушевались. Арифметика не имела своего Евклида; на это звание не могут претендовать ни Эратосфен, ни Никомах, ни арабские алгебраисты, ни Леонард Пизанский, ни Лука Пачиоли. Учение о делимости целых чисел есть единственный вопрос, который получил в древности теоретическую разработку и притом в тех же «Началах» Евклида, в геометрической форме. Самая задача о логическом обосновании начал арифметики имеет очень позднее происхождение. Все руководства по арифметике носили на себе отпечаток книги Луки Пачиоли и имели практический характер. Но в XIX в. вопрос об обосновании арифметики чрезвычайно занял внимание математиков и притом с двух точек зрения. Во-первых, к этому привели замечательные изыскания в области основ геометрии, которые мы изложили выше. Замечательные результаты логического и гноселогического характера, которые этими изысканиями были достигнуты, с одной стороны, естественно, вызывали интерес к тому, как решаются те же вопросы в области арифметики, — а с другой стороны, как мы видим, они непосредственно уперлись в арифметику. Во-вторых, к тем же вопросам привели также задачи анализа чисто фактического, можно сказать, догматического характера.

Как известно, со второй половины XVII ст. начинается необычайный подъем в области математики и точного знания вообще. Идеи Декарта к этому времени уже успели получить полное развитие, а Лейбниц и Ньютон в эту пору заложили основы исчисления бесконечно малых (см.). Необычайно обильный запас новых средств математического исследования, который таился в идеях Лейбница и Ньютона, быстро разросся в мощное здание математического анализа. Труды братьев Бернулли, Тейлора, Стирлинга, Маклорена, Эйлера, Лагранжа, Лапласа, Монжа, Лежандра, наконец, Коши, Гаусса и Якоби — дали такие средства математического исследования, по сравнению с которыми творения древних геометров казались детским лепетом. Но, как это часто бывает, сильный взмах научной волны выбросил много нового материала, недостаточно проверенного, недостаточно установленного. Более того, углубленное исследование стало обнаруживать прямые ошибки в трудах первоклассных геометров. Многие результаты, представлявшиеся бесспорными, оказались справедливыми только в известных пределах; от других пришлось и вовсе отказаться. Самый метод бесконечно малых по своим особенностям представляет много искушений для поспешных выводов. Он требует очень тщательного обоснования, чтобы его выводы действительно были безукоризненными; вне этого условия он иногда приводит к нелепым результатам. Это обстоятельство порождало в первые десятилетия непримиримых врагов нового исчисления, в числе которых были такие выдающиеся математики, как Каталан и Ролль. Позднее, когда анализ развернулся, никто не мог огульно отрицать его значения; но тем сильнее становилась тенденция подвергнуть новые методы тщательной критике и так их обработать, чтобы поставить анализ бесконечно малых на совершенно твердые основания. Коши и Гаусс были уже видными представителями этих тенденций, Вейерштрасс дал этим требованиям яркое выражение. Но основы анализа, как обнаружено тщательными исследованиями, коренятся глубоко в началах арифметики, и выполнение задач, поставленных Коши, Гауссом и Вейерштрассом, требует разработки теоретических оснований арифметики.

Наряду с анализом бесконечно малых была еще одна дисциплина, правильная постановка которой настоятельно требовала выяснения основоначал арифметики: это было учение о комплексных числах. Самый термин «комплексное число» был введен Гауссом только в 1813 г., а утвердился гораздо позже. Господствовал термин «мнимое число», который не вышел из употребления еще и по сей день. Между тем эта точка зрения на комплексные числа, как на «мнимые», несуществующие числа, служила источником неисчислимых споров, сомнений и ошибок. Чтобы пролить полный свет и на это орудие математического исследования, нужно было дать себе отчет в том, что такое число вообще. Чтобы дать строго научное построение теории комплексных чисел, необходимо было сначала выяснить теоретические основания арифметики «действительных» чисел, как их называют, следуя той же неудачной терминологии. Немало трудностей представило и обоснование учения об иррациональности и даже обоснование отрицательных чисел. Вся история алгебры проникнута стремлением рассеять туман, окружавший все эти основные орудия математического исследования. Эту задачу выполнили Грассман, Шредер, Гамильтон, Дедекинд, Кантор и др.

20. Арифметика Грассмана. В арифметике интуиция играла еще большую роль, нежели в геометрии. Здесь формальное обоснование дисциплины даже не намечалось, пока настоятельная потребность в этом не была выдвинута развитием анализа. Первые твердые шаги в этом направлении были сделаны Германом Грассманом (см.).

В 1844 г. вышло его «Учение о линейном протяжении  («Die lineare Ausdehnungslehre»). Идеи этого замечательного сочинения в его первоначальном виде (в 1862 г. он выпустил совершенно переработанное издание того же сочинения) весьма расплывчаты; но, по существу, в них заложены основы конвенционалистического мировоззрения и формального обоснования математики. Сочинение начинается вступлением, определяющим весь его характер. Мы приводили уже выше (ст. 406') эти вводные слова. С той же точки зрения Грассман в другом сочинении, «Учебник арифметики» (1861), подходит к началам арифметики. Книга содержит обоснование учения о целых и дробных числах; однако, наиболее ценным является учение о целых числах, не только сохранившееся до сих пор, но являющееся наиболее прочным обоснованием арифметики.

В основе грассмановой арифметики лежит натуральный ряд, т. е. ряд терминов; (слов), символов (знаков), следующих друг за другом в определенном порядке в том смысле, что каждому члену этого ряда всегда соответствует определенный последующий член, и каждому члену, кроме начального, соответствует определенный предшествующий член; член натурального ряда, следующий за членом а, будем обозначать через а'. Существенно важное значение при этом имеют два обстоятельства: во-первых, ряд должен быть неограниченным, т. е. за каждым членом всегда должен следовать, некоторый член; во-вторых, все члены ряда должны быть различны, ни один из  них не может повториться. Элементы, или члены такого ряда мы и будем рассматривать как числа (целые числа); точнее: под числами (мы будем пока иметь ввиду только целые числа) мы будем разуметь члены натурального ряда. Начальный член натурального ряда будем обозначать символом 0, следующий символом 1; для каждого члена натурального ряда должно быть установлено наименование и обозначение; допустим, что это возможно сделать и что это осуществлено.

В элементарной математике мы встречались с приемом доказательства, известным под названием совершенной индукции. Чтобы доказать закон составления подходящих дробей непрерывной дроби, показывают, что закон этот справедлив, для второй, для третьей дроби; затем доказывают, что, буде он справедлив для k-ой дроби, он справедлив также для (k + 1)-ой дроби; отсюда заключают: он справедлив для 2-ой дроби, следовательно, — он справедлив для 3-й: будучи справедлив; для 3-й дроби, он должен быть справедлив для 4-ой и т. д., т. е. он справедлив для каждой дроби. Этот прием применяется и во многих других случаях. Грассман не только обнаружил, что в арифметике натурального ряда все доказательства, могут быть проведены методом совершенной индукции, но показал, что все основные определения могут быть установлены: тем же приемом.

Пусть а будет произвольный член натурального ряда. Под символом а + 0 условимся разуметь то же число а; это мы выразим равенством:

Под символом а + 1 условимся разуметь тот член натурального ряда, который следует за а. В соответствии с обозначением, уже принятым выше, это соглашение можно выразить равенством:

Смысл его ограничивается тем, что под символами а + 1 и а' мы условливаемся разуметь одно и то же, а именно — член натурального ряда, следующий за а.

Равенства (1) и (2) выражают определения, устанавливающие значение двух новых символов: а + 0 и а + 1. Составление по числу а чисел а + 0 и а + 1 называют также прибавлением к числу а числа 0 или, соответственно, числа 1.

Предыдущие определения можно выразить так: прибавить к натуральному числу а нуль значит взять то же число; прибавить 1 — значит взять следующий член натурального ряда.

Необходимо отметить один принцип, который лежит в основе как этих, так и всех дальнейших определений в том смысле, что гарантирует невозможность логической ошибки, из этих определений проистекающей. Он заключается в следующем: если мы вводим новый символ, или термин, который раньше не имел никакого значения, то мы можем условиться разуметь под этим символом, или термином, любой ранее установленный объект. На этом праве именовать любой объект произвольным термином, или обозначать его любым символом, не имеющим иного значения, и на законе совершенной индукции основана вся арифметика. Содержание этого принципа отчетливо оттеняет условный, конвенциональный характер дисциплины; мы будем называть его принципом свободного обозначения.

Итак, равенства (1) и (2) устанавливают значение символов а + 0 и а + 1, или, иначе, устанавливают, что значит прибавить к натуральному числу 0 или 1. Мы могли бы аналогично определить, что значит прибавить к натуральному числу 2 (число,  следующее за 1), 3 и т. д. Но чтобы этим путем установить, что значит прибавить  любое число, нужно было бы сделать бесчисленное множество соглашений, установить бесчисленное множество определений вида (1) и (2). Закон совершенной индукции приходит здесь на помощь. Допустим, что мы установили, что значит прибавить к натуральному числу а число n, т. е. установили значение символа а + n. В таком случае условимся под символом a + (n + 1) разуметь число, следующее за а + n, т. е. число (а + n)'. Это можно выразить равенством:

Смысл этого нового определения заключается в том, что оно устанавливает, как прибавить (что значит прибавить) число,  следующее за n, т. е. число (n + 1), коль скоро известно, что значит прибавить число n. Но равенства (1) и (2) устанавливают, что значит прибавить число 0 или число 1. Поэтому равенство (3) устанавливает, что значит прибавить число, следующее за 1 (т. е. 2); но в таком случае равенство (3) устанавливает, что значит прибавить число, следующее за 2 (т. е. 3), затем число, следующее за 3, и т. д. Методом совершенной индукции равенство (3) вместе с предшествующими ему равенствами (1) и (2) устанавливает, что значит прибавить к натуральному числу а любое число n. Такого рода определение, устанавливаемое методом совершенной индукции, называется индуктивным определением. Введя индуктивные определения, Грассман заложил прочный фундамент научной арифметики, прежде всего — арифметики натурального ряда.

Так как равенства (1), (2) и (3) содержат исчерпывающее определение символа а + b (т. е. исчерпывающее определение суммы или операции, при помощи которой она вычисляется, — сложения), то все свойства суммы должны в этих равенствах содержаться, или, иначе, должны логически из них вытекать. Грассман показал, что все свойства суммы двух целых чисел действительно можно вывести из соотношений (1) — (3), пользуясь опять-таки законом совершенной индукции. Покажем это на том свойстве суммы, которое известно под названием закона сочетательности (или ассоциативности). Оно выражается равенством:

При с = 0, в силу определения (1), как левая, так и правая часть этого равенства обращается в а + b; теорема, таким образом, справедлива. При с = 1 равенство имеет вид:

В силу определения (3) левая часть этого равенства выражает число натурального ряда (a+b)' т. е. следующее за а+b. В силу определения (2) тот же член натурального ряда выражается правой частью равенства. Равенство остается, следовательно, справедливым и при с = 1. Допустим, что оно справедливо при с = n, т. е., что имеет место равенство:

Докажем, что теорема справедлива также при с = n + 1, т. е., что имеет место равенство:

В силу установленного уже соотношения (4)

а потому

Из того же соотношения (4) следует:

В силу сделанного допущения, которое выражается равенством (5), правая часть последнего равенства равна [(a+b)+n]+1. Итак, преобразование левой части равенства (6) через соотношения (7), (8) и (9) приводит к равенству:

Согласно тому же соотношению (4)

Равенства (10) и (11) показывают, что обе части равенства (6) выражают один и тот же член натурального ряда, а потому равенство это справедливо. Вместе с тем индуктивно по отношению к с доказано соотношение (I), т. е. сочетательность суммы. Мы подробно привели это доказательство для того, чтобы отчетливо выяснить, каким образом Грассман применяет метод совершенной индукции. Совершенно тем же путем Грассман устанавливает второй основной закон сложения, который выражается равенством

и известен под названием закона переместительности (или коммутативности). Из этих двух основных законов можно вывести все остальные свойства сложения, заключающиеся в том, что можно слагаемые соединять в какие угодно группы, складывать слагаемые каждой группы в каком угодно порядке, а затем сложить полученные частные суммы; результат (общая сумма) не зависит ни от группировки слагаемых, ни от порядка их расположения в каждой сумме; и это устанавливается индуктивно по отношению к числу слагаемых.

Исчерпав, таким образом, теорию сложения целых чисел, Грассман переходит к вычитанию. Если а есть число натурального ряда, следующее за b или совпадающее с b, то всегда существует один и только один член натурального ряда х, для которого

Это доказывается индуктивно по отношению к b. Число х называется разностью чисел а и b и обозначается символом а—b; этот символ определяется соотношением

Определив, таким образом, понятие о разности и вычитании, Грассман устанавливает свойства суммы и разности, выражающиеся равенствами:

Отсюда проистекают дальнейшие свойства суммы и разности, выражающиеся известными правилами сложения и вычитания многочленов. Каждый шаг в этой теории неизменно проводится методом совершенной индукции.

Умножение целых чисел Грассман определяет также индуктивно. Прежде всего, равенства

представляют собою определения, устанавливающие, что: под произведением натурального числа на нуль мы разумеем нуль; под произведением натурального числа на 1 мы разумеем то же число. За этим следует индуктивное определение, выражаемое равенством

Смысл его заключается в следующем. Предполагая известным, что разумеют под произведением натурального числа а на натуральное число n (т. е. а·n), оно устанавливает, что мы разумеем под произведением а·(n+1); именно, под произведением числа а на число (n+1) мы разумеем произведение а·n, увеличенное числом а. Из этого определения, неизменно путем совершенной индукции, выводятся три основных свойства умножения: переместительность произведения, сочетательность его и распределительность относительно суммы, которые последовательно выражаются равенствами:

Из этих свойств выводятся все арифметические преобразования, известные под названием умножения одночленов и многочленов.

Для перехода к делению необходимо установить еще одно очень важное свойство, заключающееся в следующем:

иными словами, если произведение двух множителей равно нулю, то, по крайней мере, один из сомножителей равен нулю.

Если число а следует за числом b в натуральном ряду, то говорят, что а больше b (в знаках а > b) и что b меньше а (b < а). Из основной теоремы о существовании разности следует, что при а > b

где с > 0 (ибо при с = 0 мы имели бы а = b).

Теперь легко доказать, что при а > b и b, отличном от нуля, всегда существует одна и только одна пара чисел m и r, удовлетворяющих соотношениям:

Число m называется частным, а число r — остатком от деления числа а на число b. Из этого определения разматывается все учение о делении целых чисел, включая сюда и учение о делимости, т. е. о случаях деления, в которых остаток равен нулю.

В изложенном заключается вся грассманова арифметика натурального ряда. Сформулируем теперь, в чем заключается сущность этого учения.

1) Точкой отправления служит натуральный ряд, который считается как бы заданным, известным.

2) Над членами натурального ряда (целыми числами) устанавливаются операции, определения которых выполняются методом совершенной индукции.

3) Путем совершенной индукции из этих определений выводятся основные арифметические законы I—V.

4) Из этих основных законов строго формально выводятся все преобразования суммы, разности, произведения и частного (целого).

5) Целые числа рассматриваются только как символы, входящие в состав натурального ряда.

6) Безукоризненная логика арифметики покоится на двух принципах: на принципе свободного обозначения и принципе совершенной индукции.

Грассман не ограничивается тем материалом, который мы привели выше. Он строит также арифметику целых отрицательных чисел, разматывая ее одновременно с учением о натуральном ряде^*). Он, далее, строит арифметику дробных и иррациональных чисел. Но учение о дробях у Грассмана уже значительно слабее, а учение об иррациональных числах никакой ценности не имеет. Заслуга Грассмана заключается в том, что он построил строго научную арифметику натурального ряда и тем заложил фундамент не только научной арифметики, но и всего анализа.

^*) Грассман фактически оперирует с двусторонним натуральным рядом, неограниченно простирающимся как в одну сторону (положительную), так и в другую (отрицательную).

21. Учение о рациональных числах. В предыдущей главе мы уже говорили о том, при каких условиях один член натурального ряда считается больше или меньше другого. Остановимся теперь на этом подробнее. Натуральный ряд, как нечто готовое, заданное, как мы видели, служит основанием всей грассмановой арифметики. Он представляет собой ряд символов, расположенных в определенном порядке. Учением об операциях над целыми числами (членами натурального ряда) для каждого целого числа установлено множество символов, его выражающих; так, например, число 15 можно выразить также символами 13 + 2, 10 + 5, 3·5, 17—2,... Будем теперь через N обозначать натуральный ряд, черев M — совокупность всех символов, которыми в силу соглашений, установленных арифметикой целых чисел, члены натурального ряда могут быть обозначаемы; это есть, таким образом, комплекс, или многообразие, в том смысле, как это понятие установлено в ст. величина (см. IX, 346/50) и в главе 20 настоящей статьи.

Пусть m и m' будут два элемента многообразия M, т. е. два символа, обозначающие члены натурального ряда N. Мы будем говорить, что m равно m' (m=m'), если символы m и m' выражают один и тот же член натурального ряда (одно и то же целое число). Мы будем говорить, что m больше m' (m > m'), если m означает член натурального ряда, следующий за m', и что m меньше m' (m < m'), если m означает член натурального ряда, предшествующий члену m'. Понятия «равно», «больше» и «меньше», этим путем установленные, удовлетворяют постулатам сравнения (см. IX, 348/50). Правда, это связано с нашими представлениями о тождестве и последовательности. Так, например, транзитивность понятия «больше», сводящаяся к тому, что при m > m', m' > m'' имеет место соотношение m > m'', вытекает из того, что член m последовательности, следующий за членом m', который, в свою очередь, следует за членом m'', необходимо следует также за членом m''. Этого мы не доказываем; мы здесь апеллируем к понятию более общему, лежащему за пределами арифметики.

Этими соотношениями совокупность целых чисел претворена в величину. Строго говоря, называя члены натурального ряда целыми числами, мы до некоторой степени предвосхищаем историческую эволюцию понятия о числе. Понятие это в первой своей формации, как в историческом его развитии, так и в ходе теоретической конструкции, возникает как член натурального ряда, а затем расширяется — эволюционирует.

Первым этапом в ходе этой эволюции является введение дробей. У Грассмана это выполнено неудачно; Э. Шредер (Schröder) и О. Штольц (Stolz) провели учение  о дробях совершенно строго; мы изложим здесь сущность этого учения.

Пусть m и n будут два натуральных числа, из которых второе отлично от нуля. Мы построим из них новый символ, скомбинировав их так или иначе. Совершенно безразлично, как графически этот комбинированный символ изображать: ему можно придать вид ^m/_n, или m/n, или m:n, или даже (m, n). Будем придерживаться наиболее принятых обозначений ^m/_n, или m/n.

Этого рода символы мы будем называть дробями, число m — числителем, число n —  знаменателем дроби: согласно основному условию, знаменатель всегда отличен от нуля.

Совокупность дробей мы претворим в величину. Для этого мы должны установить критерии сравнения, т. е. соглашения относительно того, при каких условиях мы будем считать одну дробь равной другой, больше или меньше другой дроби. Пусть m/n и m'/n' будут две дроби. Составим произведения mn' и m'n; если mn' = m'n, то мы будем говорить, что дробь m/n равна дроби m'n' (m/n = m'/n'); если mn' > m'n, мы будем говорить, что дробь m/n больше дроби m'/n' (m/n > m'/n'); если mn' < m'n, то мы будем говорить, что дробь m/n меньше дроби m'/n’ (m/n < m'/n'). Наше право установить эти соглашения основано на том, что они удовлетворяют всем восьми постулатам сравнения. В самом деле, одно из трех соотношений mn' = m'n, mn' > m'n и mn < m'n всегда имеет место, причем  первое исключает два других, как это установлено для целых чисел. Следовательно, для всяких двух дробей m/n и m'/n, имеет место одно из соотношений: m/n = m /n', m/n > m'/n', m/n <  m'/n', причем первое исключает два других; это значит, что первые три постулата сравнения удовлетворены. Докажем теперь транзитивность равенства дробей. Пусть m/n = m'/n' и m'/n' = m''/n'', это значит: mn' = m'n и m'n'' = m''n'. Равенство двух целых, чисел не нарушается, если оба члена равенства умножить на одно и то же целое число. Умножая обе части первого равенства на n'', а второго на n, получим mn'n'' = m'nn'', m'nn'' = m''nn'. Отсюда вследствие транзитивности равенства целых чисел получим: mn'n'' = m''nn', а так как n' отлично от нуля, то отсюда следует: mn'' = m''n, т. е. m/n = m''/n''. Таким же образом докажем транзитивность соотношений «больше» и «меньше» для дробей, а также возвратность и обратимость равенства. Все постулаты сравнения соблюдены, и совокупность дробей, таким образом, претворена в величину. Критерий сравнения двух дробей можно еще выразить следующим образом. Числитель первой дроби и знаменатель второй будем называть крайними членами сравниваемых дробей, а знаменатель первой и числитель второй — средними членами. Соглашение, установленное для сравнения дробей, сводится к тому, что первая дробь равна второй, если произведение крайних членов равно произведению средних; первая дробь больше второй, если произведение крайних больше произведения средних, первая дробь меньше второй, если произведение крайних членов меньше произведения средних.

Согласно основному условию, знаменатель дроби может быть равен также, т. е. среди дробей имеются также дроби вида m/1 с любым числителем m. Условимся под дробью m/1 разуметь целое число т, т. е. под символом m/1 условимся разуметь то же, что и под символом m. Вследствие этого соглашения совокупность дробей включает в себя все целые числа. Дроби образуют, таким образом, комплекс, часть которого составляют целые числа. Их поэтому также называют числами, но в отличие от исключительно целых чисел их называют рациональными числами. Переход от целых чисел к рациональным представляет собой, таким образом, первый шаг, первый этап в ходе эволюции понятия о числе.

Далее, из критериев сравнения вытекает, что дробь не меняет своего значения, если числитель и знаменатель ее умножить или разделить на одно и то же число. Точнее, если числитель и знаменатель дроби умножить или разделить на одно и то же число, то мы получим дробь, равную исходной. Это вытекает из того, что для двух дробей mр/nр и m/n произведение средних членов всегда равно произведению крайних. На этом предложении в обычном порядке основывается сокращение дробей и приведение их к общему знаменателю. В частности, отсюда вытекает, что всякая дробь m/n, в которой числитель представляет собою число, кратное знаменателя, так что m=n.k, представляет собою целое число; в самом деле, m/n = nk/n = k/1 = k.

Теперь уже нетрудно перейти к действиям над дробями. Пусть m/n и m'/n' будут две дроби. Приведем их к общему знаменателю. Получим:

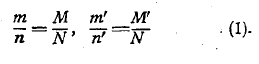
Дробь

мы будем называть суммой данных дробей. Здесь возникает только один вопрос. Заданные две дроби могут быть и иначе приведены к одному знаменателю. Мы можем наряду с соотношениями (1) получить:

а тогда сумма выразится дробью

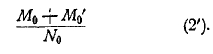
Будет ли дробь (2') равна дроби (2)?

Легко обнаружить, что это действительно имеет место. В самом деле, из соотношений (1) и (1') вытекает:

а потому

Складывая эти равенства почленно, получаем:

Это последнее соотношение обнаруживает, что дроби (2) и (2') равны. В этом смысле данное выше определение устанавливает понятие о сумме однозначно.

Мы дали определение суммы двух дробей; но слагаемые могут иногда представлять собою целые числа. Совпадает ли тогда сумма двух дробей, устанавливаемая выражением (2), с суммой этих целых чисел? Легко видеть, что это имеет место. Если дроби m/n и m'/n', равны целым числам k и k', то

Итак, определение суммы двух дробей установлено таким образом, что всякий раз, как дроби эти сводятся к целым числам, сумма их, вычисленная по правилу сложения дробей, равна сумме, составленной по правилу  сложения целых чисел. В силу этого свойства новое определение удовлетворяет т. н.  закону перманентности.

Теперь нетрудно показать, что основные  свойства суммы целых чисел, выражаемые соотношениями (I) и (II), остаются в силе  и для дробей. В самом деле:

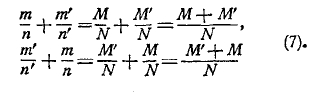
Но по свойству суммы целых чисел

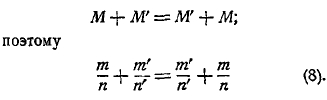
Так доказывается переместительность суммы; так же доказывается ее сочетательность. Раз установлены основные законы и) и (II), то и остальные свойства суммы, формально из них проистекающие, также остаются в силе.

Разность двух дробей устанавливается так же, как и для целых чисел: именно, доказывается, что при m/n > m'/n' существует дробь x/y, удовлетворяющая соотношению

Если этому требованию удовлетворяют две дроби

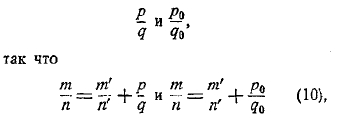
то p/q = p₀/q₀. Дробь х/у, этим соотношением определяемая, называется разностью двух данных дробей. Без труда доказывается, что разность дробей обладает свойствами, выраженными соотношениями (III).

Далее, произведение двух дробей определяется соглашением:

В словах это выражается следующим образом. Под произведением двух дробей мы разумеем дробь, числителем которой служит произведение числителей, а знаменателем — произведение знаменателей данных дробей. Попытки доказать соотношение (II) имеют смысл только в том случае, когда раньше как-либо иначе установлено определение произведения двух дробей.

Определив таким образом произведение двух дробей, нетрудно доказать, что остается в силе закон перманентности, т. е. что в том случае, когда дроби сводятся к целым числам, произведение их равно произведению этих целых чисел. Последний шаг заключается в том, что доказывают, что основные свойства произведения, выражаемые соотношениями (IV) и (V), также остаются в силе. Вследствие этого все формальные преобразования одночленов и многочленов, установленные для целых чисел, остаются в силе и для дробей.

В этом заключается сущность эволюции понятия о числе. Понятие о числе расширяется: устанавливается более обширный комплекс чисел, содержащий в себе прежний как частный случай. В этом расширенном комплексе устанавливаются основные арифметические операции с соблюдением закона перманентности и основных законов формальных преобразований.

Этим расширением числовой области достигается важное преимущество. В области целых чисел деление на целое число вообще неосуществимо; это значит: если а и b суть два целых числа (члены натурального ряда), то не всегда существует целое число х, удовлетворяющее соотношению

Напротив того, существование такого числа составляет только исключение, которое мы характеризуем термином: а кратно b. Между тем для дробей такое число всегда существует:

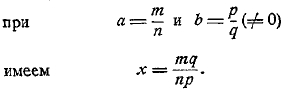
Разыскание числа х (деление) представляет собою действие, обратное умножению в том смысле, что по результату умножения и одному из данных для умножения чисел (сомножителей) разыскивается другое число (другой сомножитель).

Есть существенная разница между установлением т. н. прямых операций — сложения и умножения — и обратных. Первые определяются для целых чисел индуктивно, для дробей формально — соглашениями (2) и (11). В том и в другом случае определение содержит непосредственно алгорифм действия, т. е. определенные правила, на основании которых по двум данным числам можно разыскать сумму и произведение данных чисел. Определения обратных действий — вычитания и деления — такого алгорифма не содержат. Ставится задача, решением которой определяется разность и частное двух чисел. Но задача не всегда имеет решение. В области целых чисел часто не решается ни задача о вычитании, ни задача о делении. Расширение числового материала до области рациональных чисел приводит к тому, что одна из этих операций, деление, оказывается всегда осуществимой.

22. Учение об арифметических числах. К числу прямых операций — сложению и умножению — присоединяется третья операция: возвышение в степень. Грассман определяет это действие для всякого рационального а соглашениями:

После того, что выше было изложено, вряд ли нужно объяснять, что равенства (1) выражают индуктивное определение степени (конечно, с целым показателем): первое из  них устанавливает, что под символом а¹ мы будем разуметь самое число а; второе устанавливает, что под символом a^m+1 мы разумеем произведение числа а^m на а. Основные соотношения

легко выводятся из определений (1). Но введение этой новой прямой операции непосредственно приводит и к обратной, к извлечению корня. Здесь задача заключается в том, чтобы по данному рациональному числу А и целому числу m найти такое число х, при котором

В области рациональных чисел эта задача допускает решение только в исключительных случаях. Уже пифагорейцам было известно, что √2 не выражается рациональным числом. Доказательство этого предложения мы находим и у Евклида, которого к идее об иррациональных величинах приводят соображения чисто геометрического характера. В самом деле, процесс разыскания общей меры двух отрезков естественно приводит к идее несоизмеримых отрезков, отношение: которых не выражается рациональным числом. Теорема Пифагора дала для этих размышлений новый материал. Так называемый «египетский треугольник», катеты которого равны 3 и 4, а гипотенуза равна 5, послужил, по-видимому, наводящим указанием для открытия основного соотношения между сторонами прямоугольного треугольника. Когда это соотношение было установлено, то равнобедренный прямоугольный, треугольник, катеты которого равны 1 длины, приводил к разысканию числа √2, которым должна в этом случае выражаться гипотенуза. Эта именно задача привела уже пифагорейцев к сознанию, что не всякий отрезок выражается рациональным числом. Для Евклида это обстоятельство является  одним из основных вопросов в деле обоснования геометрии. Решению этого вопроса посвящены две книги «Начал» — пятая, содержащая теорию пропорций, и десятая, непосредственно посвященная иррациональным величинам. Из тех затруднений, которые возникали на почве решения вопроса о несоизмеримости значений геометрической величины, выход был двоякий: либо нужно было расширить числовую область, чтобы получить числовой материал, с помощью которого было бы возможно всякий отрезок выражать числом (иначе говоря, с помощью которого можно было бы выразить числом отношение любых двух отрезков), либо отказаться от выражения отрезков и других геометрических величин числами. Евклид становится на вторую точку зрения. Он делает это бессознательно, потому что идея расширения числовой области, идея иррационального числа, ему совершенно чужда; и благодаря этому в греческой геометрии утверждается строгий принцип «geometriam geometrice», о котором мы уже упоминали выше. В главе, посвященной «Началам», говорилось, что теория пропорций, изложенная в V книге и по замыслу принадлежащая Евдоксу, представляет собою одно из величайших творений греческого гения. По существу, мы здесь имеем совершенно строгую теорию иррациональных чисел; но нужно отчетливое понимание существа вопроса, чтобы это усмотреть в геометрическом построении, в которое теория облечена. Десятая книга, также чрезвычайно замечательное построение тонкой геометрической мысли, содержит учение об иррациональных отрезках, построяемых по данным отрезкам циркулем и линейкой; выражаясь арифметически, можно сказать, что эта книга содержит учение об иррациональных числах, выражающихся через квадратные корни.

Но метрическая геометрия, которая в приложениях имела наиболее важное, почти исключительное значение, неизбежно требовала арифметизации, введения числа для выражения результатов измерения, в том числе и иррациональных чисел для выражения значений величины, несоизмеримых с принятой единицей. Однако, как теория пропорций (V книга), так и учение об иррациональных величинах (Х кн.) у Евклида очень сложны и доступны только людям с очень развитой и тонкой логикой. Вследствие этого учение об иррациональном числе проложило себе в средние века иной путь. Иррациональные числа появляются в литературе не только без достаточного обоснования, но и без удовлетворительного определения. Ощупью, интуитивно их вводят средневековые математики — арабские, итальянские, германские — то как «глухие числа» («numeri surdi», Леонард Пизанский), то как «потенциальные числа» («numeri in potential Региомонтан), то, как корни из рациональных чисел (преимущественно Лука Пачиоли); Штифель, который вводит в первый раз термин «иррациональное число», сопровождает это свое нововведение замечанием: «irrationalis numerus non est numeras». И вопреки всякой логике, в силу необходимости, по пути интуиции эти «числа, не представляющие собою чисел», проникли во все сочинения по арифметике; с развитием же анализа у Декарта, Лейбница, Ньютона они получили совершенно прочное, утвердившееся место в науке.

Таким образом, иррациональные числа, как все основные идеи математики, завоевали себе место сначала без достаточного обоснования. Только в эпоху ревизионизма, в середине XIX ст., вопрос острогом обосновании учения об иррациональном числе был поставлен на очередь и получил исчерпывающее разрешение в работах Вейерштрасса (см.), Кантора и Дедекинда (см.). Система Дедекинда получила, благодаря значительно большей простоте и отчетливости, исключительное распространение. Мы постараемся, поэтому, выяснить здесь его идею. Свою систему Дедекинд изложил в мемуаре «Непрерывность и иррациональные числа»¹⁾. Введение к отдельному изданию этого небольшого, но замечательного, сочинения настолько освещает сущность и значение вопроса, что мы считаем нужным, поместить здесь первые два абзаца целиком.

«Рассуждения, составляющие предмет этого маленького сочинения, относятся к осени 1858 г. Тогда я, в качестве профессора Союзного политехникума в Цюрихе, в первый раз обязан был по своему положению излагать элементы дифференциального исчисления и при этом чувствовал живее чем когда-либо недостаток в действительно научном обосновании арифметики. При изложении понятия о приближении переменной величины к постоянному пределу, и именно при доказательстве того положения, что величина, которая возрастает постоянно, но не сверх всяких границ, должна приближаться к некоторому пределу, я прибегал к геометрической наглядности. Да и теперь я из дидактических оснований считаю такое привлечение геометрической наглядности при первом обучении дифференциальному исчислению; необычайно полезным, даже неизбежным, если не хотят потратить слишком много времени. Но никто не станет отрицать того, что этот способ введения в изучение дифференциального исчисления не может иметь никакого притязания на научность».

¹⁾ «Stetigkeit und Irrationale Zahlen», 1872. В 1923 г., выпущено четвертое русское изд.: Дедекинд, «Непрерывность и иррациональные числа», Одесса, Матезис.

 «Во мне тогда это чувство неудовлетворенности преобладало в такой степени, что я принял твердое решение думать до тех  пор, пока не найду чисто арифметического и вполне строгого основания для начал анализа бесконечных. Говорят часто, что дифференциальное исчисление занимается непрерывными величинами; однако же нигде не дают определения этой непрерывности и даже при самом строгом изложении дифференциального исчисления доказательства не основывают на непрерывности, а апеллируют более или менее сознательно либо к геометрическим представлениям, либо к представлениям, которые берут свое начало в геометрии, либо, наконец, основывают доказательства на положениях, которые сами никогда не были доказаны чисто арифметическим путем».

Итак, Дедекинд прежде всего связывает введение понятия об иррациональном числе с обоснованием идеи о непрерывности. В чем же заключается связь между этими понятиями?

Если мы возьмем луч, т. е. часть прямой линии, расположенную по одну сторону от некоторой «начальной» точки О, то между его элементами, — точками, и рядом рациональных чисел существует аналогия; точки луча по мере удаления от его начальной точки следуют друг за другом в определенном порядке подобно тому, как следуют друг за другом возрастающие рациональные числа. Относительно каждых двух точек луча М и М' можно сказать, которая из двух следует за другой; и если точка М’ следует за М, а точка М'' следует за М', то и точка М'' следует за М (транзитивность понятия «следует»). В соответствии с этим находится и наше представление о прямой, как о ряде следующих друг за другом точек. Точно так же рациональные числа образуют аналогичный ряд: из двух различных чисел m и m' одно больше другого, и если m' > m, а m'' > m', то m'' > m (транзитивность понятия «больше»). Эта аналогия служила основанием для тех геометрических соображений, на которые, как указывает Дедекинд, приходится опираться при изучении числового ряда.

Но между рядом точек на луче и рядом рациональных чисел есть и существенная разница. Когда точка М продвигается вдоль по лучу от его начальной точки, то отрезок ОМ постоянно возрастает, как возрастают элементы числового ряда — рациональные числа. Если принять определенный отрезок за единицу, то можно будет измерять отрезки или выражать их числами; при этом каждому рациональному числу m будет отвечать такая точка М, что отрезок ОМ будет выражаться числом m. Но обратное не имеет места: не всякий отрезок ОМ выражается рациональным числом. В ряду рациональных чисел не хватает чисел для выражения длины всякого отрезка. Если, например, от вершины О отложить на луче отрезок, равный гипотенузе равнобедренного прямоугольного треугольника с рациональным катетом, то конечной точке этого отрезка никакое рациональное число отвечать не будет. Ряд точек прямой обильнее, нежели ряд рациональных чисел; несмотря на густоту последнего (между любыми, сколь угодно близкими, двумя рациональными числами содержится бесчисленное множество других рациональных чисел), в нем есть пробелы — он не непрерывен. Задача, которую себе поставил Дедекинд, заключалась, прежде всего, в том, чтобы эти пробелы, это отсутствие непрерывности констатировать, не прибегая к геометрической аналогии. Вот как он достигает этой цели.

Ряд рациональных чисел может быть многообразно рассечен на две группы таким образом, чтобы каждое число одной группы было больше каждого числа другой группы. Например, мы можем отнести к первой группе все рациональные числа, не превосходящие 4, а ко второй все числа, большие 4; ясно, что при этих условиях каждое число второй группы превышает любое число первой группы. Такое расщепление ряда рациональных чисел Дедекинд называет сечением.

Существо дела заключается в том, что возможны два рода сечений. Приведенный пример представляет собою сечение первого рода; оно характеризуется тем, что первая группа имеет последний (наибольший) элемент 4. Естественно, что вторая группа крайнего элемента уже не имеет: в нее входят числа, большие 4; наименьшего среди них уже нет. Можно число 4 перенести во вторую группу; тогда первая группа не будет иметь последнего (наибольшего) элемента, но вторая будет иметь первый (наименьший) элемент. Характерным для этого сечения является, следовательно, то обстоятельство, что существует элемент (число 4), который может завершить первую группу или начать вторую. Можно выделить это число из обеих групп и сказать, что оно это сечение производит в том смысле, что оно как бы разделяет ряд натуральных чисел на две группы: к одной относятся числа, большие его, к другой — меньшие; самое же это число мы можем отнести либо к одной, либо к другой группе. Такого рода сечения мы будем называть замкнутыми, а пограничное для обеих групп число будем называть замыкающим. Есть, однако, сечения иного рода, в которых замыкающего числа нет. Если, например, разделить все рациональные числа на две группы, относя к первой все числа, квадраты которых меньше 2, а ко второй все числа, квадраты которых больше 2, — то ни первая, ни вторая группа замыкающего числа не имеют: нет наибольшего числа в первой группе, нет наименьшего числа во второй группе; в самом деле, произведя приближенное извлечение квадратного корня, мы можем получить неограниченный ряд приближенно меньших значений (квадраты их будут меньше 2-х) и неограниченный ряд приближенно больших значений (квадраты их будут больше 2-х). Такого рода сечения мы будем называть разомкнутыми, или открытыми.

Ряд рациональных чисел имеет, как мы сказали, пробелы; эти пробелы в том и заключаются, что не существует чисел, которые замыкали бы открытые сечения; и чтобы эти пробелы восполнить, чтобы сделать ряд непрерывным, нужно ввести новые числа, которые все открытые сечения замыкают. В этом заключается идея Дедекинда. Он осуществляет ее следующим образом.

В области рациональных чисел, как мы видели, возможно, бесчисленное множество сечений. С каждым сечением будем соединять новое понятие, графически — новый символ, который будем называть арифметическим числом. Какое дать этим символам начертание, дело второстепенное; мы будем этот символ выбирать в каждом случае спорадически, в зависимости от сечения, с которым он соединяется.

Пусть теперь х и у будут два арифметических числа; первое образуется сечением (Х, Х’), второе — сечением (Y, Y’); при этом мы разумеем, что в группу Х включены меньшие, в группу Х' - большие числа; то же относится к группам Y и Y. Может случиться, что сечение (Х, Х') совпадает с сечением (Y, Y'); в таком случае мы будем говорить, что арифметическое число х равно арифметическому числу у (х=у). Если это не имеет места, то либо группа Х содержит числа, которых нет в Y, либо, наоборот, группа Y содержит числа, которых нет в Х; в первом случае мы будем говорить, что х > у, во втором что x < у. Очень легко показать, что постулаты сравнения при этих соглашениях удовлетворены и что совокупность арифметических чисел этим путем превращена в величину.  Каждое арифметическое число связано с некоторым сечением. Если сечение (Х, Х'), производящее арифметическое число х, замыкается некоторым рациональным числом m/n, то мы будем отождествлять х с рациональным числом m/n (т. е. будем считать х=m/n); иными словами, под символом х мы будем в этом случае разуметь рациональное число m/n.

Вследствие этого соглашения комплекс арифметических чисел содержит в себе все рациональные числа. Арифметические числа, связанные с открытыми сечениями (т. е. не замыкаемыми рациональными числами), мы будем называть иррациональными. Комплекс арифметических чисел является, таким образом, более мощным, чем комплекс рациональных чисел; переход от рациональных чисел к комплексу арифметических чисел представляет новый этап в деле эволюции понятия о числе.

Пусть (А, А') будет некоторое разомкнутое сечение ряда рациональных чисел, которое воспроизводит иррациональное число а. Пусть α — рациональное число, принадлежащее группе А. Сравним числа а и α, т. е. постараемся определить, которое из них больше. Чтобы воспользоваться установленным выше критерием, мы должны обратиться к тому сечению (А, А'), которое производит число α. Так как α есть число рациональное, то это последнее сечение есть замкнутое: оно замыкается самим числом α, которое мы можем считать наибольшим числом группы А. Так как число а принадлежит группе А, которая не замкнута, то в последней имеются числа, превосходящие α. Иными словами, группа А составляет часть группы А, а потому α < а. Таким же образом докажем, что α > а, если α есть любое число группы А'. Итак, иррациональное число а, определяемое сечением (А, А'), больше всякого (рационального) числа группы А и меньше всякого числа’ группы А'; оно в этом смысле замыкает сечение (А, А’). Иррациональные числа, таким образом, заполняют все пробелы в ряду рациональных чисел и делают его непрерывным. Мы говорили до сих пор о сечениях в ряду рациональных чисел, но, если теперь таким же образом рассечь ряд всех арифметических чисел, то такое сечение всегда замыкается арифметическим числом. В этом заключается непрерывность ряда всех арифметических чисел. Цель, которую себе поставил Дедекинд, достигнута.

Теперь остается установить общие правила действий над арифметическими числами. Пусть (А, А') и (В, В') будут два сечения, производящие два арифметических числа а и b. Пусть а будет произвольное число группы А, β — произвольное число группы В. Теперь составим сечение (С, С'), относя в группу С всякое число вида α + β (т. е. всякое рациональное число, представляющее собой сумму одного числа группы А и одного числа группы В), а также всякое другое рациональное число, которое меньше какого-либо числа α + β. Таким же образом в группу С войдут все рациональные числа, которые больше любого числа α + β. Арифметическое число с, которое этим путем получается, т. е. определяется сечением (С, С'), будем называть суммой чисел а и b:

c = a + b

Положим, в частности, что а и b суть рациональные числа. Тогда а можно рассматривать как наибольшее число группы А, а b — как наибольшее число группы В. Ясно, что в этом случае а + b, т. е. сумма рациональных чисел а и b, как мы ее определили раньше, будет наибольшим числом группы С. Сечение (С, С') в этом случае замыкается рациональным числом а + b, представляющим собою сумму чисел а и b в том смысле, как мы ее определили выше. Число а + b замыкает сечение (С, С'), оно им определяется как арифметическое число. Иными словами, если два арифметических числа сводятся к числам рациональным, то сумма, новым определением установленная, совпадает с суммой этих чисел, установленной арифметикою рациональных чисел. В этом заключается закон перманентности, который мы выяснили выше.

Остается показать, что формальные законы арифметических операций остаются в силе для всех арифметических чисел. Мы не можем здесь на этом останавливаться; читатель, уяснивший себе сущность задачи, справится с этим сам. В области арифметических чисел все арифметические операции, которые выполняются для рациональных чисел (сложение, вычитание, когда уменьшаемое больше вычитаемого, умножение и деление, когда делитель отличен от нуля), также выполняются и следуют тем же формальным законам. Таков неизменный ход эволюции понятия о числе.

Но в области всех арифметических чисел выполняется также большое число таких операций, которые в области рациональных чисел остаются невыполнимыми. Самой важной из этих операций является извлечение корня. Пусть а будет какое угодно арифметическое число, а n — целое число. Если а есть рациональное число, то рациональное число х, удовлетворяющее уравнению хⁿ=а, существует только в исключительных случаях; если а есть иррациональное число, то такого числа х в области рациональных чисел и искать невозможно. Но в области всех арифметических чисел такое число всегда существует. В самом деле, положим, что рационального числа х, удовлетворяющего соотношению хⁿ=а, не существует. Разобьем все рациональные числа на две категории, относя к первой всякое число х', для которого х'ⁿ < а, а ко второй категории — всякое число х'', для которого х'' ⁿ > а. Ясно, что число второй категории больше всякого числа первой категории; мы получим, таким образом, дедекиндово сечение, которое замыкается числом х. Путем несложных рассуждений, которых мы не будем здесь приводить, можно показать, что хⁿ = а. Но не только этот простой сравнительно  вопрос разрешается введением иррациональных чисел. Является возможным установить понятие о степени с любым показателем. Учение о пределах получает прочную базу (хотя оно возможно и в области рациональных чисел). Непрерывность числового ряда дает возможность установить понятие о непрерывности функции; становится возможным показать, что непрерывная функция, переходя от одного значения к другому,  необходимо принимает все промежуточные значения. В геометрии получает разрешение вопрос об измерении; отношение любых двух отрезков выражается рациональным или иррациональным числом (равно как отношение двух любых значений какой угодно величины); вопрос об отношениях и пропорциях теряет свою трудность.

23. Относительные (положительные и отрицательные) числа. Введение иррациональных чисел сделало возможным целый ряд операций, которые без того были невыполнимы. Можно сказать, что благодаря введению иррациональных чисел, получили точное разрешение проблемы, которые до того допускали лишь приближенное решение. Но оставалась операция, о разрешении которой, казалось, не могло быть речи по существу: это было вычитание большего числа из меньшего. В тесной связи с этим стояла задача о решении линейного уравнения с одной неизвестной; эта задача иногда допускала решение, иногда такового не допускала; последнее имело место в тех случаях, когда уравнение — по современной терминологии — имело отрицательный корень. Но проницательный глаз математика усмотрел возможность выйти из этого затруднения задолго до того, как сделалось возможным провести эту идею строго сознательно, чтобы не сказать — строго логически и научно. Правда, греческим геометрам, которые, как мы видели выше, построили глубоко продуманные учения об иррациональных величинах, идея отрицательного числа была совершенно чужда. Даже Диофант, творец греческой алгебры, обнаруживший столько проницательности в решении сложных задач арифметического характера, всегда подчиняет коэффициенты линейного уравнения таким условиям, при которых оно имеет положительное решение, и квалифицирует как άδύνατον (невозможное) всякое уравнение, этим условиям не удовлетворяющее. Идея о положительных и отрицательных числах появляется, прежде всего, у индусов (Брахмагупта, см.; VII ст. н. э.). Они появляются здесь в качестве «имущества» и «долга» и даже иногда для обозначения противоположных направлений на прямой. Отрицательные числа отмечаются точкой над числом. И все же другой индусский математик Бхаскара (см.), живший в XII ст., говорит, что «люди не одобряют абсолютных отрицательных чисел» (слово «абсолютных» нужно, по-видимому, понимать как «отвлеченных»).  Арабы совершенно отвергают отрицательные числа, их еще не знает и Леонард Пизанский. Но в XVI ст. отрицательные числа уже твердо прокладывают себе путь. Французский математик Шюке (Chuquet, в конце XV ст.) оперирует отрицательными числами уже довольно смело. Но совершенно решительно становится на этот путь Михаил Штифель (Michael Stilel). В своем  сочинении «Arithmetica integra» (1544) он помещает особую главу, носящую заглавие «De signis additorum et substractorum et de numeris absurdis». Рассуждения, которые Штифель приводит, настолько любопытны и характерны, что мы приведем некоторые извлечения из них (в переводе профессора И. Ю. Тимченко).

«Правило умножения и деления, поскольку оно касается умножения, обнимает четыре различных случая следующего рода:

поскольку же оно касается деления, оно обнимает четыре подобных же различных случая».

«Ты видишь, конечно, что все это с первого взгляда очень похоже на самый пустой вздор; и однако же выполненные сообразно с этим алгебраические действия приводят к изобретениям, поистине  удивительным. Но чтобы не пропустить ничего из того, что относится к целостной системе арифметики, по мере своих сил я должен, как мне кажется, сказать в этом месте о воображаемых числах ниже нуля».

«Подобно тому, как мы представляем себе различные корни из чисел, не имеющих таких корней, и это представление оказывается в высшей степени полезным в применении к математике, так же не без пользы представляют себе и числа ниже нуля».

«Таким образом, искусство счета ввиду неограниченности запаса своих средств обычно пользуется и тем, что существует, и тем, что лишь представляется как существующее. Ибо, подобно тому, как выше  единицы полагаем целые числа, а ниже единицы представляем себе доли единицы, так выше нуля полагаем единицу с числами и ниже нуля представляем себе тоже единицу и числа».

«По этому поводу можно было бы написать целую новую книгу о чудесных свойствах чисел; но я должен от этого воздержаться и уйти с закрытыми глазами».

И все же великий творец современной алгебры Виет (см. II, 91/94) еще совершенно отрицает возможность введения отрицательных чисел.

Полное право гражданства отрицательные числа получили только со времени Декарта; без них аналитическая геометрия Декарта была бы невозможна, и могущественное значение идей Декарта в области геометрии повлекло за собой признание отрицательных чисел. Лейбниц, Ньютон, Даламбер, Маклорен, Ролль, наконец, Эйлер положили отрицательные числа в основу алгебры на равных правах с положительными, сделали их совершенно неизбежным средством математического исследования, и возражения против введения их в математику замолкли. Но это не значит, что введение отрицательных чисел было действительно обосновано. Напротив, это потребовало еще многих усилий. К обоснованию учения о положительных и отрицательных числах есть два пути: один был указан Грассманом, другой тщательно проведен Штольцем.

Как мы видели, естественным фундаментом всей арифметики служит учение о целых числах. Основная идея Грассмана заключается в том, что учение о целых отрицательных числах должно быть построено одновременно с учением о целых положительных числах. С этой целью он продолжает натуральный ряд в противоположную сторону. Ведь, по существу, основой учения Грассмана служит то обстоятельство, что натуральные числа представляют собой элементы расположенного ряда; этот ряд начинается с некоторого элемента, который мы обозначаем символом 0, за которым следуют элементы 1, 2, 3, Мы дополним ряд элементами, предшествующими элементу 0; именно, элемент, непосредственно предшествующий элементу 0, мы обозначим через —1, ему предшествующий — через —2, ему предшествующий — через —3 и т. д. Получается двусторонний ряд; элементы, следующие за элементом 0, будем называть положительными числами, а элементы, предшествующие элементу 0, будем называть отрицательными числами; самое число нуль можно относить к обеим категориям или ни к одной из них. Признаком того, что натуральное число m больше числа n, мы считали то обстоятельство, что оно следует за числом n в натуральном ряду; и наоборот, следовательно, m < n означает, что число m предшествует числу n в натуральном ряду. Это соглашение распространим на все члены двустороннего ряда; иными словами, во всем двустороннем ряду будем считать число m большим, чем число n, или меньшим, чем оно, смотря по тому следует ли m за n, или предшествует ему. Вследствие такого соглашения всякое отрицательное число меньше нуля; это имеет лишь то содержание, что отрицательное число предшествует нулю в двустороннем натуральном ряду. Чтобы отличать числа, следующие за нулем (положительные), от предшествующих нулю (отрицательных), первые отмечаются знаком +, вторые — знаком —. Эти определения не содержат в себе ничего неотчетливого и лишают учение об отрицательных числах какого бы то ни было мистического элемента, который так пугал математиков ранней поры.

Теория действий над элементами двустороннего натурального ряда (положительными и отрицательными целыми числами) развивается совершенно так же, как и учение об арифметическом натуральном ряде, изложенное в главе 20. Разница заключается лишь в том, что как индуктивные определения, так и индуктивные доказательства должно вести в двух направлениях, распространяя содержащуюся в них идею в обе стороны натурального ряда. Так, сложение определяется индуктивно соотношениями:

где а' есть член натурального ряда, следующий за а. В новых обозначениях эти соглашения, относящиеся только к положительным числам, должны быть написаны следующим образом:

К этим соотношениям должны быть теперь присоединены, в качестве определения, равенства:

Первое из них устанавливает, что придать к числу а' отрицательную 1 значит взять предшествующий член ряда. Во втором равенстве, после этого соглашения, n + (— 1) есть член натурального ряда, непосредственно предшествующий числу n, а (a + n) + (— 1) есть член ряда, непосредственно предшествующий числу (a + n). Поэтому при n > 0 равенство (2b) выражает теорему, которая может и должна быть доказана. При n = 0 равенство (2b) совпадает с (2а); при n<0 оно представляет собою индуктивное определение того, что значит прибавить отрицательное число. Для того, чтобы для двойного ряда при помощи совершенной индукции доказать некоторое предложение, нужно обнаружить, что всякий раз, как предложение это оказывается справедливым для некоторого числа а, оно справедливо также для следующего числа а+(+1) и для предыдущего а+ (— 1). Эти две части доказательства обычно очень мало отличаются одна от другой. Рассуждения, таким образом, несколько усложняются; но зато получается база, на которой учение о положительных и отрицательных числах можно строить одновременно.

Позднейшие авторы, главным образом Штольц, идут другим путем. К учению о положительных и отрицательных числах они приступают после того, как учение о всех арифметических числах уже построено. Это имеет ту хорошую сторону, что соответствует историческому ходу эволюции понятия о числе. Самое построение выполняется следующим образом.

В связи с каждым арифметическим числом а введем два новых символа (термина, понятия) +а и —а; первое будем называть положительным числом, второе отрицательным; арифметическое число а будем называть абсолютным значением обоих чисел. Таким образом, над комплексом арифметических чисел надстраивается двойной комплекс чисел — положительных и отрицательных. Прежде всего, этот комплекс нужно претворить в величину, т. е. нужно установить критерии сравнения. Это достигается следующими соглашениями.

1) Два положительных числа или, соответственно, два отрицательных числа мы будем считать равными, если равны их абсолютные значения.

2) Из двух неравных положительных чисел мы будем считать большим то, абсолютное значение которого больше.

3) Из двух неравных отрицательных чисел мы будем считать большим то, которое имеет меньшее абсолютное значение.

4) Всякое отрицательное число меньше всякого положительного.

5) Числа +0 и —0 равны и имеют то же значение, что их абсолютное значение нуль.

6) Нуль меньше всякого положительного числа и больше всякого отрицательного числа.

Что эти критерии сравнения удовлетворяют постулатам сравнения, обнаружить чрезвычайно легко.

Полученная таким образом величина образует новый комплекс, элементы которого прежде, в отличие от арифметических чисел, стали называть алгебраическими числами. Термин этот, однако, оказался неудачным, так как в алгебру пришлось ввести алгебраические числа в ином значении этого слова. В настоящее время можно считать утвердившимся термин «относительные числа», введенный Штольцем и получивший, можно сказать, всеобщее признание. Числа со знаками являются относительными по сравнению с арифметическими числами, представляющими собой их абсолютные значения.

Теперь нужно установить правила арифметических действий над относительными числами. Определение сложения положительных и отрицательных чисел выражается следующими равенствами:

Словесное выражение этих соглашений совпадает с тем, что мы привыкли называть правилом сложения положительных и отрицательных чисел. Иными словами, скажем, правило «чтобы сложить два числа, имеющие одинаковые знаки, нужно сложить их абсолютные значения и при сумме поставить тот же знак» нужно рассматривать как определение того, что мы уславливаемся разуметь под суммой двух положительных или двух отрицательных чисел.

Из этих определений легко вывести, что основные свойства суммы арифметических чисел (законы сочетательности и переместительности) остаются в силе и для относительных чисел. Материал, которым арифметика оперирует, расширяется, а законы операций остаются те же. Это — общая идея, которая лежит в основе всего хода эволюции понятия о числе.

Из определения суммы, именно из того, которое выражается соотношением 3), вытекает, что (+ а) + (—а) = 0; иными словами, сумма двух чисел, имеющих одинаковые абсолютные значения, во противоположные знаки, равна нулю. На практике нам часто приходится иметь дело с так называемыми противоположными величинами, т. е. с такими величинами, которые при соединении в равных количествах могут быть опущены из счета. Таковы имущество и долг, повышение и понижение и т. д. Соотношения между этими величинами удобно передаются, если выражать их положительными и отрицательными числами, относя положительные числа к элементам одной величины, а отрицательные к противоположной. Эти общеизвестные соображения служили руководящей нитью при введении положительных и отрицательных чисел. Но существо дела все же заключается в том, что расширение числового комплекса есть условное соглашение, построенное на логической базе, а конкретные величины представляют собой объекты, к которым эти числа применяются; для этих именно применений условные постулаты и созданы; но они от этого не перестают быть условными построениями.

Вычитание определяется как действие, обратное сложению; иными словами, определение вычитания относительных чисел не отличается от определения вычитания арифметических чисел: по идее это то же действие. Но в области относительных чисел всяким двум числам отвечает разность независимо от того, которое из данных чисел служит уменьшаемым и которое вычитаемым. Если, например, даны два положительных числа (+а) и (+b), то

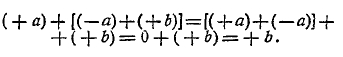
Таким образом, число (—а) + (+b), или, что то же, (+ b) + (—а), есть разность чисел ( + b) и (+ а), каковы бы ни были абсолютные значения этих чисел. То же имеет место, каковы бы ни были уменьшаемое и вычитаемое, в том смысле, что вычесть положительное число все равно, что прибавить отрицательное число с тем же абсолютным значением, и обратно. А так как сложение двух относительных чисел всегда осуществляется однозначно, то однозначно осуществляется и их вычитание.

Умножение относительных чисел определяется четырьмя равенствами:

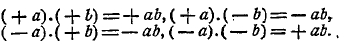
Эти равенства обычно рассматриваются как «правила» перемножения положительных и отрицательных чисел, выводимые из их значения. Эти выводы основываются на конкретных применениях отрицательных чисел; они всегда полны натяжек, обусловливаемых тем, что за факт выдается то, что есть чистое соглашение. Когда же соглашение, которым определяется умножение относительных чисел, установлено, то из него действительно выводятся основные свойства произведения — законы переместительности, сочетательности и распределительности. Все формальные преобразования остаются, поэтому, в силе. Дальнейшее развитие учения об относительных числах уже не представляет затруднений; таким образом, и этот этап в ходе эволюции понятия о числе закончен.

Отметим еще один момент. Положительные числа часто отождествляются с арифметическими числами. Логический смысл этого заключается в том, что под символом + а мы разумеем то же, что под символом а. Против этого нельзя возражать с точки зрения логической. Но более стройной является система Штольца, рассматривающая арифметические числа только как материал, из которого строятся  положительные и отрицательные числа. В тех случаях, когда мы оперируем со значениями одной величины, находят себе применение только арифметические числа; когда приходится иметь дело со значениями двух противоположных величин, получают применение относительные числа.

25. Комплексные числа. С введением отрицательных чисел получилась область, в которой рациональные операции (сложение, вычитание, умножение и деление на число, отличное от нуля) всегда выполнимы. Но за то извлечение корня четной степени — прежде всего квадратного — из отрицательных чисел стало невозможным. Стремление выйти из этого затруднения привело к введению комплексных чисел, по существу завершившему эволюцию числовой области. Выше мы довольно подробно изложили историю блуждания мысли в процессе установления понятия о положительных и отрицательных числах. Мы не имеем возможности остановиться хотя бы столь же подробно на таких же блужданиях, которыми сопровождалось построение учения о комплексных числах. Эти блуждания были еще глубже, еще продолжительнее и сопровождались ошибками. Оно и понятно: иррациональные и отрицательные числа при своем появлении имели под собою конкретный субстрат, т. е. геометрические и реальные объекты, соотношения которых они выражали; более того, необходимость выражать такого рода соотношения и привела к введению этого рода чисел. Между тем, комплексные числа долгое время оставались совершенно абстрактным творением человеческого ума.

Как и в ходе возникновения отрицательных чисел, комплексные числа появляются сначала как нечто фиктивное (numeri ficti), воображаемое (nombres illusoires), мнимое (imaginaire). И по настоящее время относительные числа сохраняют свое наименование только в противоположение арифметическим числам. В противоположение же комплексным, или, как их прежде называли, мнимым числам, их называют действительными числами, иногда вещественными числами. Действия над комплексными числами долгое время выполняются ощупью, часто неудачно. Итальянские алгебраисты XVI в., Кардан («Ars magna», 1545) и  Бомбелли («Algebra», 1572), впервые пользуются отчетливо мнимыми числами. Ив. Бернулли, Лейбниц, Муавр вводят их в анализ (XVII ст.), Гаусс и Коши развертывают применения их, которые дают комплексным числам доминирующее значение. Но научное обоснование самой арифметики комплексных чисел принадлежит Гамильтону (1837; см.) Мы здесь изложим основы теории комплексных чисел по Гамильтону.

Из каждых двух действительных чисел а и b, как-либо их скомбинировав, скажем, — в виде (а, b), составим символ. Иначе говоря, составим из действительных чисел все возможные размещения по два, и каждое такое размещение вида (а, b) будем называть составным, или комплексным числом. Это суть размещения, а потому комплекс (а, b) нужно отличать от комплекса (b, а). Действительные числа а и b можно называть компонентами комплексного числа (а, b). Среди комплексных чисел будут числа вида (а, 0), т. е. числа, вторая компонента которых равна нулю. Каждое число вида (а, 0) мы будем отождествлять с действительным числом а; иными словами, под символом (а, 0) мы будем разуметь то же, что под символом а; это будет новое обозначение того же действительного числа. При этом соглашении в состав совокупности всех комплексных чисел войдут, все действительные числа, и введение комплексных чисел представляет собою поэтому новое обобщение понятия о числе.

Два комплексных числа (а, b) и (а', b') мы будем называть равными, если первые и вторые компоненты их соответственно равны между собою. Иными словами;

Установленное таким образом понятие о равенстве обладает всеми свойствами, которые должны быть равенству присущи: оно возвратно (т. е. каждое комплексное число равно самому себе), обратимо и транзитивно. Можно установить и условия, при которых одно комплексное число считается большим или меньшим, чем другое. Так, можно считать число (а, b) большим комплексного числа (a, b'), если разность а — а' есть положительное число, и меньшим, если эта разность есть число отрицательное; если же эта разность равна нулю, то вопрос на тех же основаниях решается по разности b — b'. Эти критерии удовлетворяют всем постулатам сравнения. Однако, по характеру применения комплексных чисел, значение имеет только условие их равенства.

Под суммой двух комплексных чисел мы разумеем комплексное число, первая  компонента которого равна сумме первых  компонент слагаемых, а вторая компонента равна сумме вторых компонент слагаемых. Иными словами, сумма двух комплексных чисел определяется равенством:

Из этого явно вытекает, что основные свойства суммы действительных чисел остаются в силе и для суммы комплексных чисел. Так, например:

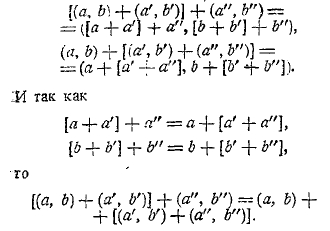
нить некоторые весьма несложные вычисления.

Закон сочетательности остается, следовательно, в силе.

Разность двух комплексных чисел, в ее обычном определении, всегда существует и однозначно определяется соотношением:

ибо, согласно определению суммы двух  комплексных чисел:

В определении умножения двух комплексных чисел лежит центр тяжести их значения. Произведение двух комплексных чисел  определяется равенством:

иными словами, под произведением двух комплексных чисел (а, а') и (b, b') мы разумеем комплексное число, первой компонентой которого служит число аа' — bb', а второй — число ab' + а'b. При всей своеобразности этого определения, оно все же приводит к тому, что все формальные преобразования произведения сохраняют свою силу. Так, например, достаточно посмотреть на правую часть последнего равенства,  чтобы убедиться, что она не меняется, когда мы переставим сомножители левой части равенства. Чтобы обнаружить, что законы сочетательности и переместительности остаются в силе, необходимо выполнить некоторые весьма несложные вычисления.

Наконец, деление комплексных чисел определяется однозначно в тех случаях, когда делитель отличен от нуля.

Мы получаем, таким образом, вновь расширенную область чисел, в состав которой действительные числа входят как частный случай; именно, к действительным числам, как мы установили выше особым соглашением, принадлежат те, и только те, комплексные числа, вторые компоненты которых равны нулю. Если два комплексных числа сводятся к действительным числам, то их сумма, разность, произведение и частное совпадают с суммой, разностью, произведением и частным тех же чисел, как они установлены арифметикой действительных чисел. Так, равенства (2) — (4) в этом случае дают:

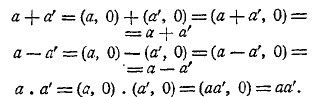
Новые определения строго следуют закону перманентности. Но в этой расширенной числовой области получают осуществление операции, которые в области вещественных чисел невыполнимы. Это легко обнаружить.

Число (1, 0), по установленному выше соглашению, есть действительная единица (1). Комплексное число (0, 1) обозначим через і:

его часто называют мнимой единицей.

Если теперь, следуя определению (4), вычислим произведение і.і, то получим:

Итак, комплексное число (0, 1), обозначенное нами через і, в силу установленного выше определения произведения, обладает тем свойством, что i² = — 1. Извлечение квадратного корня из отрицательной 1 становится возможным: именно, числа і и —і т. е. (0, 1) и (0,-1) являются двумя корнями квадратными из —1. Вместе с тем квадратные корни из любого действительного отрицательного числа —а выражаются комплексными числами і√а и —і√а, т. е. числами (0, √а), (0, —√а).

Мало того, в области комплексных чисел оказывается выполнимым извлечение корня любой степени из любого числа. Еще более: в этой области всякое алгебраическое уравнение n-ой степени, каковы бы ни были его коэффициенты, имеет n корней. Только благодаря этому свойству алгебра комплексной области отличается такой цельностью и стройностью.

Теперь нетрудно, пользуясь основными определениями (1), (2) и (4), установить следующее тождество:

Вследствие принятых выше соглашений и обозначений, это тождество можно написать в виде

Каждое комплексное число может быть представлено в виде а.1 + bi. Это интерпретируют так, что каждое комплексное число составлено из действительной единицы, взятой с коэффициентом а, и из мнимой единицы, взятой с коэффициентом b. Отсюда и наименование «комплексное число». Самое обозначение (a, b) можно оставить, заменив его через а + bi. Этот символ можно рассматривать как сумму комплексных чисел и соответственно этому оперировать с комплексными числами по правилам формальной алгебры, заменяя множитель i² везде, где мы к нему придем, через —1. Это, конечно, и служило наведением при определении произведения двух комплексных чисел, выражаемого равенством (4): в самом деле, перемножая числа а+bі и а'+b'і по этому правилу, мы получим число (аа'—bb') + (ab' + bа') i = (aa' — bb', ab' + а'b), как того требует определение (4).

В области комплексных чисел, как мы уже указали выше, выполняются все операции классической алгебры. Такая совокупность чисел, в которой все рациональные операции выполняются и приводят в результате к числу той же совокупности, называется числовым корпусом. Совокупность всех арифметических чисел не представляет собою числового корпуса, хотя в ней осуществляются даже иррациональные операции. Совокупность всех рациональных относительных чисел уже образует числовой корпус, но в нем неосуществимы иррациональные операции. Совокупность всех относительных чисел образует числовой корпус, в пределах которого осуществляются многие иррациональные операции, — но не все. Совокупность всех комплексных чисел есть числовой корпус, в котором получают осуществление все алгебраические операции. Современная алгебра есть алгебра корпуса всех комплексных чисел.

Но эволюция, приведшая к корпусу комплексных чисел, оказалась необычайно плодотворной не только в области алгебры. Все изучение функций, теория функций, как мы теперь говорим, оказалось неизмеримо плодотворнее, когда областью задания функции явился корпус комплексных чисел. Введение комплексных чисел — это не этап в ходе эволюции учения о числе, это целая эпоха, и из этой эпохи математика еще не вышла.

25. Векторы и высшие комплексные числа. При всем своем значении комплексные числа оставались только формальным средством алгебраического вычисления. Не было конкретного субстрата, к которому они получили бы применение, а потому они все же занимали в арифметике исключительное место. С возникновением учения о векторах это положение изменилось (см. векториальный анализ). Вектор на плоскости определяется двумя проекциями на оси ортогональных координат; эти проекции называются компонентами, или слагающими вектора. Два вектора (Х, Y) и (Х', Y') заданные своими компонентами, равны, если Х = Х' и Y = Y'. Сумма векторов имеет своими компонентами Х + Х' и Y + Y'. Условимся теперь выражать комплексным числом Х + Yі вектор, имеющий компонентами Х и Y. В таком случае равные комплексные числа выражают равные векторы, сумма (разность) двух комплексных чисел выражает вектор, представляющий собой сумму (разность) двух векторов, которые выражаются данными двумя комплексными числами. Таким образом, между комплексными числами и векторами на плоскости устанавливается соответствие, дающее возможность соотношения между векторами выражать соотношениями между комплексными числами. Эта идея, проведенная, вернее, — намеченная Коши, послужила импульсом к всеобщему признанию комплексных чисел. При всем том область применения комплексных чисел к векторам на плоскости остается очень ограниченной: только сумма и разность комплексных чисел действительно выражает сумму и разность векторов. Произведение комплексных чисел не может выразить геометрического произведения двух векторов, потому что это последнее произведение выражается вектором, не лежащим в той же плоскости, а перпендикулярным к ней. Арифметический аппарат, в полной мере воспроизводящий операции над векторами, был создан в другом порядке идей, в ходе дальнейшего развития идеи о комплексном числе. Если обыкновенное комплексное число составлено из двух независимых единиц, то естественно было идти в этом направлении дальше, построить алгебру высших комплексных чисел, составленных из большего числа независимых единиц. Это почти одновременно было выполнено Грассманом в Германии и Гамильтоном в Англии.

Комплексное число Грассмана имеет вид

a₁e₁ + a₂e₂ + a₃e₃ + … + a_ne_n,

где e₁, e₂,…, e_n суть независимые единицы, а коэффициенты при них а₁, а₂,…, а_n (компоненты комплексного числа) суть действительные числа. Сумма и разность двух высших комплексных чисел определяется так же, как сумма и разность обыкновенных комплексных чисел, т. е. путем сложения и вычитания соответствующих компонент. Вместе с тем сумма и разность высших комплексных чисел следует тем же формальным законам, что и сумма и разность действительных чисел. Но дать такое определение произведению высших комплексных чисел, при котором и оно следовало бы формальным законам арифметики действительных чисел, не удавалось. В разрешении этой задачи Грассман и Гамильтон шли совершенно различными путями: Грассман шел в порядке экстенсивной алгебры, в которой произведение двух комплексных чисел является комплексным числом более высокого порядка; Гамильтон шел в направлении интенсивной алгебры, в которой произведение двух комплексных чисел есть комплексное число, составленное из тех же независимых единиц, что и сомножители. Осуществление интенсивной алгебры¹⁾, сохраняющей все основные законы арифметики действительных чисел, не удавалось. Вейерштрасс показал, что это коренится в существе задачи: построить  более мощную интенсивную алгебру, т. е. алгебру высших комплексных чисел, сохраняющую все формальные законы арифметики действительных чисел, невозможно. Вот почему с введением обыкновенных комплексных чисел эволюция учения о числе получила завершение. Образования  более поздние и более сложные следуют уже иным законам: закон перманентности падает.

¹⁾ Было бы правильнее говорить не об экстенсивной и интенсивной алгебре, а об экстенсивной и интенсивной арифметике. Мы отдаем дань установившейся, хотя и неправильной терминологии.

Как мы видели, сумма высших комплексных чисел определяется таким образом, что компоненты суммы являются суммами соответствующих компонент слагающих. Интенсивная алгебра, построенная на этих началах, называется линейной алгеброй. Трудность эволюции линейной алгебры, как мы видели, заключается в определении произведений. Во всех системах линейной алгебры закон распределительности все же  остается в силе (как это имеет место и при перемножении векторов), затруднение же составляют, главным образом, два пункта: закон переместительности и, как теперь часто говорят, закон аннулирования.

Отступления от закона переместительности в различных системах линейной алгебры обыкновенно заключаются в том, что произведение двух сомножителей меняет свой знак с перестановкой этих двух сомножителей. Закон аннулирования в арифметике обыкновенных комплексных чисел заключается в том, что произведения обращаются в нуль в том и только в том случае, когда в нуль обращается один из сомножителей. В более сложных системах произведение может обращаться в нуль, когда ни один из сомножителей не равен нулю.

Из линейных систем высших комплексных чисел наиболее замечательной является алгебра кватернионов, построенная Гамильтоном (см. кватернионы). При помощи кватернионов могут быть выражены векторы трехмерного пространства, но общая область кватернионов шире, нежели область векторов: общее выражение кватернионов содержит, кроме векторной, так называемую скалярную часть; но операции над теми кватернионами, которые служат для выражения векторов, вполне следуют законам векторной алгебры.

27. Закон совершенной индукции. Предыдущий очерк дает сжатую, но достаточно полную картину эволюции понятия о числе. Как мы видим, в основе изложенной системы арифметики лежит натуральный ряд. Комбинируя натуральные (целые) числа попарно, мы составляем дроби, т. е. строим систему всех рациональных чисел. Заполняя пробелы между рациональными числами, т. е. вводя числа, замыкающие всякое сечение в области рациональных чисел, мы создаем систему всех арифметических чисел. Из арифметических чисел мы образуем относительные (положительные и отрицательные) числа и таким образом приходим к корпусу всех действительных чисел. Наконец, комбинируя попарно действительные числа, мы составляем комплексные числа, образованием которых, как уже было сказано, эволюция в известном смысле заканчивается. Операция над дробными числами всегда сводится к тем или иным операциям над членами дроби, т. е. над целыми числами; операции над иррациональными числами выполняются путем действий над рациональными числами, которые образуют соответствующее сечение; наконец, операции над относительными числами всегда сводятся к действиям над арифметическими числами, операции над комплексными числами — к действиям над действительными числами. Таким образом, в конечном счете, операции над любыми числами сводятся к операциям над целыми числами. Кронекер (Kronecker, 1823—1891) совершенно прав, когда утверждает, что вся эволюция арифметики заключается в развитии учения о целом числе.

В основе учения о целом числе лежат две основные идеи: понятие о последовательности и закон совершенной индукции. Дж. Пеано (родился 1858) сводит те свойства натурального ряда, на которых основано все учение о целых числах, а, следовательно, и вся арифметика, к следующим пяти положениям:

1) 0 есть член натурального ряда.

2) Каждому члену отвечает один, и только один, следующий член.

3) Два различных числа не могут иметь одного и того же следующего числа.

4) 0 не является следующим за каким-нибудь членом ряда (т. е. 0 есть начальный член ряда).

5) Закон совершенной индукции.

Само собой разумеется, что под числом здесь следует разуметь целое число — член натурального ряда.

Пятое положение играет в этой системе основных посылок до некоторой степени ту же роль, что и пятый постулат Евклида в геометрии. Оно сложнее остальных, оно по содержанию своему носит совершенно иной характер. Между тем оно играет в грассмановой системе построения арифметики коренную роль. Эти обстоятельства повели к стремлениям пролить больше света на роль этого положения и на его связь с остальными постулатами арифметики. Эти стремления проявляются прежде всего в попытках доказать закон совершенной индукции. Эти попытки имеют свою историю, но гораздо менее продолжительную, нежели история пятого постулата. Такого рода попытку обосновать закон совершенной индукции можно найти, например, в I томе «Энциклопедии элементарной математики» Вебера и Вельштейна, посвященном арифметике и алгебре. Однако, результаты, к которым привели доказательства пятого постулата Евклида, теперь уже были налицо и, естественно, направляли мысль исследования по тому же пути. Б. Рессель (см.) и А. Уайтхед в своем сочинении «Principia Mathematica» вполне этот вопрос разрешили. Следующие соображения выясняют их точку зрения.

Рис. 25

Возьмем на прямой (рис. 25) два последовательных отрезка AX и AY. На отрезке  АХ нанесем ряд точек: А₁ — середину отрезка АХ, A₂ — середину отрезка А₁Х, А₃ — середину А₂Х и т. д. Далее, пусть В будет середина отрезка XY, В₁ — середина ВХ, В₂ — середина B₁X, В₃ — середина В₂Х и т. д. Наконец, пусть С₁ будет середина отрезка BY, С₂ — середина С₁Y, С₃ - середина С₂Y и т. Д. Таким образом, точки, обозначенные буквами А и В (с различными индексами), сгущаются с двух сторон к точке Х, а точки, обозначенные буквой С, сгущаются к точке Y. Теперь возьмем весь ряд точек, обозначенных буквами А, В и С (с различными индексами); точки Х и Y, следовательно, в этот ряд не входят. Это ряд расположенный: какие бы две точки в нем мы ни взяли, одна из них предшествует другой, а эта последняя следует за первой. Точка А начинает ряд; ей соответствует последующий элемент, но она не имеет предшествующего элемента. Каждой другой точке соответствует определенный предшествующий и определенный, последующий элемент. Совершенно ясно, что свойства натурального ряда, выражаемые постулатами Пеано 1—4, удовлетворены (точка А играет роль 0 в натуральном ряду). Но легко видеть, что закон совершенной индукции в этом ряду справедлив не будет. В самом деле, свойство, выражаемое предложением «точка (член) нашего, ряда предшествует точке Х», принадлежит точке А; если оно принадлежит какой-либо точке (члену) ряда, то оно принадлежит и следующей точке. Это свойство, однако, не принадлежит точкам, отмеченным буквами, В_i и С_i. Это обусловливается более сложной структурой нашего ряда: переходя в нем  от одного элемента A_i к следующему, мы никогда не достигнем точек B_i.

Возможны расположенные ряды, удовлетворяющие первым четырем постулатам Пеано, но не удовлетворяющие пятому; этого рода ряды мы будем называть трансфинитными. Закон совершенной индукции есть признак, отличающий натуральный ряд от трансфинитного. Не может быть, поэтому, никакой речи о доказательстве закона совершенной индукции, основанном на остальных свойствах натурального ряда. Введение его в арифметику равносильно, соглашению исключить трансфинитные ряды. Натуральный ряд есть простейший расположенный ряд, лишенный последнего члена. Он лежит в основе нашей арифметики. Можно основать арифметику, положив в ее основу более сложный, трансфинитный ряд; это даст трансфинитную арифметику. К этому мы еще вернемся.

28. Понятие о числе по Г. Кантору. Система теоретической арифметики, изложенная выше, по существу есть творение трех лиц: Грассмана, Шредера и Пеано. Характерной особенностью этой системы является то, что точкой отправления здесь служит натуральный ряд, т. е. совокупность элементов, расположенных последовательно таким образом, что имеют место следующие три положения: 1) каждому элементу соответствует один и только один следующий (точнее непосредственно следующий) элемент; 2) каждому элементу, кроме начального, соответствует один и только один предыдущий элемент, и, наконец, 3) имеет место закон совершенной индукции. Целые числа, служащие членами этого ряда, фигурируют, таким образом, в арифметике Грассмана как числа порядковые. Их количественное значение скрадывается, — по мнению Кантора (Georg Cantor, 1845—1918) — вовсе отсутствует в этой системе. Между тем не только в приложениях практического характера, но и в самой же арифметике именно количественный характер целых чисел играет очень важную, можно даже сказать, первенствующую роль. Ведь с первых же шагов мы говорим здесь: «два, три числа», «два, три слагаемых» и т. д., и вкладываем в эту терминологию не то содержание, что «два» есть член натурального ряда, следующий за членом «один», а «три» — член, следующий за членом «два»; мы вкладываем в эти термины количественное содержание, которое совершенно отсутствует в грассмановой арифметике. Это обстоятельство Г. Кантор справедливо считает настолько важным, что требует если не полной перестройки грассмановой арифметики, то существенного ее пополнения. Став на этот путь, Кантор построил теорию, не только глубоко изменившую и дополнившую арифметику Грассмана, Шредера и Пеано, но фактически составляющую в настоящее время основание теории функций действительного переменного. Долгое время эта теория была известна под названием «учения о множествах» (Mengenlehre); в настоящее время, особливо после работ Цермелло (см.), она вошла как составная часть в теоретическую арифметику и теорию функций.

Если для Грассмана точкой отправления служит натуральный ряд и лежащая в основе его идея последовательности, то для Кантора исходным пунктом служат два понятия, уже выясненные выше: понятие о множестве и понятие о сопряжении. Совокупность объектов, тем или иным признаком объединенных в одно целое, составляет «множество», или «многообразие». Много примеров многообразий мы уже рассмотрели ранее. Многообразие, или множество (по Кантору) задано, если установлен критерий, на основании которого мы относительно каждого предмета (каждого объекта нашего мышления) можем установить, составляет ли он элемент этого многообразия или нет.

В главе 10 было обстоятельно выяснено, что значит установить совершенное (однооднозначное) сопряжение одного множества с другим. Если два множества А и В могут быть приведены одно с другим в совершенное соответствие, то, по терминологии Кантора, они имеют одинаковую мощность. Если два множества не имеют одинаковой мощности, т. е., если они не могут быть связаны совершенным соответствием, но множество А может быть связано совершенным соответствием с некоторой частью множества В, то говорят, что множество А имеет меньшую мощность, нежели множество В, или, что множество В имеет большую мощность, нежели множество А. Таким образом устанавливается понятие о мощности, как о признаке, по которому мы можем судить о возможности установления однооднозначного соответствия между двумя многообразиями.

Определяя, при каких условиях множество А имеет меньшую мощность, нежели множество мы привели два критерия, совокупностью которых это понятие устанавливается: во-первых, множество А не может быть приведено в совершенное сопряжение с множеством В; во-вторых, множество А должно сопрягаться с некоторой частью множества В. На первый взгляд может казаться, что первый из этих признаков представляет собой следствие второго. В самом деле, если множество А сопрягается с частью множества В, то казалось бы, что оно вследствие этого не может быть сопряжено с множеством в его целом. Однако, это не так. Дело в том, что существуют множества, которые могут быть приведены в совершенное соответствие со своею частью. Примером этого может служить натуральный ряд. В самом деле, напишем натуральный ряд, а под ним, элемент за элементом, подпишем тот же натуральный ряд, начиная его, скажем, с элемента 5:

Каждому элементу первого ряда отнесем в качестве соответствующего стоящий под ним элемент второго ряда, и обратно. Ясно,  что оба ряда приведены этим путем в однооднозначное соответствие, между тем второй ряд представляет собой часть первого. Кантор указал, что в этом обстоятельстве коренится различие между конечными и бесконечными множествами. Это составляет большую его заслугу.

Множество называется конечным, если оно не может быть приведено в совершенное сопряжение со своею частью, и бесконечным, если такое сопряжение возможно.

Если мы от натурального ряда отсечем все члены, следующие за некоторым его элементом, то мы получим конечное множество. Это ясно для множества 1 (т. е. содержащего только первый член ряда), а для следующих множеств 1,2; 1,2,3; 1,2,3,4;... это без труда доказывается совершенной индукцией. Из этого следует, что каждое множество, представляющее собой некоторую начальную часть натурального ряда, имеет свою особую мощность; точнее, если мы составим множества:

то из этих множеств каждое следующее имеет большую мощность, чем предыдущее. Мощность каждого из этих множеств мы можем характеризовать его последним элементом. Множества (1) мы будем называть натуральными числовыми множествами; иными словами, под натуральным  числовым множеством мы будем разуметь такое множество, которое получается из натурального ряда путем отсечения всех членов, следующих за некоторым определенным его членом. Натуральное множество мы можем, таким образом, характеризовать его последним членом; например, под натуральным множеством 4 мы можем разуметь множество 1,2,3,4; вообще, под натуральным множеством n мы можем разуметь множество 1,2,3,. . ., n.

Легко видеть, что множество _*^*_*, составленное из точек, имеет ту же мощность, что и натуральное множество 3. Существуют, конечно, и разнообразные другие множества, имеющие ту же мощность; относительно каждого такого множества мы будем говорить, что оно содержит три элемента. Вообще, мы будем говорить, что множество содержит n элементов, если оно имеет ту же мощность, что и натуральное множество n. В этом заключается количественное значение натуральных чисел.

Вообще, установление соответствия между членами натурального множества и каким-либо конечным множеством М имеет двоякое значение, двоякую цель: нумерование, т. е. последовательную отметку каждого элемента множества некоторым числом, и исчисление, т. е. установление того числового натурального множества с которым множество М имеет одинаковую мощность. Эти два процесса на практике осуществляются параллельно. Нумеруя элементы конечного многообразия, т. е. отмечая его члены числами 1, 2, 3,... и заканчивая это нумерование числом n, мы устанавливаем и его мощность.

Установив, таким образом, количественное значение целых чисел, Кантор идет в этом направлении дальше. Натуральный ряд, как мы видели, представляет собою бесконечное множество. Существуют и другие множества, имеющие ту же мощность. Так, если на прямой будем последовательно откладывать, начиная от некоторой точки, равные отрезки, то конечные их точки образуют множество, имеющее мощность натурального ряда. Это и характеризуется тем, что точки эти можно последовательно перенумеровать; каждая точка получит номер, но для этого понадобятся все числа натурального ряда. В связи с этим всякое множество, мощность которого равна мощности натурального ряда, Кантор называет исчислимым множеством.

Приведем еще другие примеры исчислимых множеств. Прежде всего, совокупность всех целых положительных и отрицательных чисел представляет собой исчислимое множество. По сравнению с натуральным рядом это множество содержит «вдвое» больше чисел. Но оно все же может быть сопряжено со своею частью — с натуральным рядом чисел; это видно из следующей таблицы:

в которой каждое верхнее число сопряжено с нижним; между тем верхний ряд содержит все положительные и отрицательные целые числа, нижний — только арифметические целые числа. Верхний ряд, таким образом, перенумерован: нижние числа представляют собой номера, отнесенные верхним числам.

Результат, к которому мы пришли, можно формулировать так: если мы соединим два исчислимых ряда в один, то получим исчислимый ряд; иначе говоря, совокупность двух исчислимых рядов имеет ту же мощность, что и каждый из них в отдельности; возможность этого коренится в том, что это ряды бесконечные. Три исчислимых ряда могут быть таким же образом соединены в один исчислимый ряд, как это видно из следующей схемы: ряды

могут быть соединены в исчислимый ряд 1,—1,1*, 2,—2,2*, 3,—3,3*, 4,—4,4* ... Более того, исчислимое множество исчислимых рядов также представляет собою исчислимый ряд. Это станет ясным из следующей схемы. Таблица

представляет собою множество, составленное из исчислимого множества исчислимых рядов. Располагая элементы этой таблицы в порядке

т. е. помещая сначала элемент первой диагонали (а1), затем элементы второй диагонали (b1, a2), затем элементы третьей (c1, b2, a3), четвертой (d1, c2, b3, a4) и т. д., мы обнаруживаем, что множество (2) представляет собою исчислимый ряд. Переход от таблицы (2) к ряду (3) называют диагональным перераспределением таблицы (2). Любопытным примером, иллюстрирующим эти соображения, является то обстоятельство, что совокупность всех рациональных дробей, т. е. всех рациональных чисел, представляет собой исчислимое множество. В самом деле, совокупность рациональных чисел можно представить в виде таблицы:

Производя в ней диагональную перегруппировку, и опуская в каждой диагонали сократимые дроби, мы этим обнаружим, что все дроби могут быть перенумерованы. При сгущенности ряда рациональных чисел могло бы оказаться, что он имеет большую мощность, нежели натуральный ряд; оказывается, однако, что это не так. Кантор показал, что и совокупность иррациональных, но алгебраических чисел (т. е. удовлетворяющих алгебраическому уравнению с рациональными коэффициентами) представляет собою исчислимое множество. Мощность натурального ряда Кантор обозначил первой буквой еврейского алфавита κ. О всяком исчислимом множестве в соответствии с этой терминологией говорят, что оно имеет κ элементов; это утверждение означает, что такое множество имеет мощность натурального ряда.

Но существуют множества большей мощности. Таково множество всех арифметических чисел. Чтобы это себе уяснить, войдем в некоторые подробности относительно этого множества.

Множество всех арифметических чисел, очевидно, имеет ту же мощность, что и множество точек прямолинейного луча. Если О есть начальная точка луча ОМ (рис. 26), то каждой точке М отвечает число (абсцисса), представляющее расстояние точки М от начала, выраженное в принятой единице меры; и обратно, каждому арифметическому числу (абсциссе) отвечает одна, и только одна, точка луча; множество точек луча и множество всех арифметических чисел имеют одну и ту же мощность.

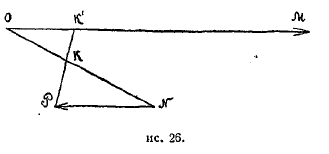
Рис. 26.

Теперь покажем, что множество точек, образующих луч ОМ, имеет ту же мощность, что и множество точек, образующих любой отрезок ON. Чтобы это обнаружить, приложим отрезок к лучу так, чтобы начало О луча совпало с началом отрезка, но чтобы они образовали некоторый угол. Затем проведем отрезок любой длины NP, параллельный лучу ОМ, но направленный в другую сторону. Из точки Р к любой точке К отрезка ON проведем луч РК, который встретит луч ОМ в точке К'. Теперь каждой точке К отрезка отнесем соответствующую точку К' луча ОМ, и обратно. Ясно, что этим каждой точке отрезка будет отнесена одна, и только одна, точка луча, а каждой точке луча — одна, и только одна, точка отрезка; конечной точке N отрезка отвечает бесконечно удаленная точка луча. Оба множества имеют, таким образом, одну и ту же мощность.

Так как точки любых двух отрезков образуют множества той же мощности, что и точки луча, то любые два отрезка, рассматриваемые как множества точек, имеют одинаковую мощность. Переводя эти результаты с геометрического языка на арифметический, мы можем сказать: совокупность всех арифметических чисел представляет собою множество той же мощности, что и совокупность чисел, содержащихся в любом интервале от а до b.

В частности, совокупность всех чисел, содержащихся между 0 и 1, имеет ту же мощность, что и совокупность всех арифметических чисел. Всякое множество этой мощности Кантор называет континуумом. Спрашивается, совпадает ли мощность континуума с мощностью натурального ряда? Если рассматривать континуум всех арифметических чисел, то натуральный ряд входит в него как составная часть; но эта часть имеет меньшую мощность. Докажем это. С этой целью допустим противное. Допустим, что совокупность всех арифметических чисел или, что то же, совокупность всех чисел, содержащихся между 0 и 1, образует исчислимое множество; иными словами, мы допустим, что все числа, содержащиеся между 0 и 1, можно перенумеровать. Каждое из этих чисел можно представить в виде десятичной дроби, конечной, если это дробь рациональная, и бесконечной, если это дробь иррациональная. Мы можем каждую дробь считать бесконечной, заполняя дальнейшие места нулями. Итак, все числа, содержащиеся между 0 и 1, перенумерованы. Составим теперь новую правильную бесконечную десятичную дробь следующим образом. После нуля поставим на первом месте десятичный знак, отличающийся на единицу (больший) от первого десятичного знака той дроби, которая имеет номер 1; на втором месте поставим цифру, на 1 превышающую ту цифру, которая занимает второе место во второй дроби; вообще на m-ом месте поставим цифру, следующую за той, которая занимает в m-ой дроби m-ое место; если эта цифра была 9, мы вместо нее поставим нуль. Полученная таким образом дробь будет отличаться от всех наших дробей: от первой она, во всяком случае, будет отличаться первым десятичным знаком, от второй — вторым и т. д. Между тем это все же правильная дробь. Так как мы допустили, что перенумерованы все дроби, то мы приходим к противоречию. Это рассуждение требует только небольшого усложнения, чтобы избежать кое-каких несущественных возражений. Итак, мощность континуума выше мощности натурального ряда. Будем обозначать ее через κ₁. Это есть число, количественный характер которого имеет то же значение, что и в случае любого числа натурального ряда. Если мы скажем что данное множество содержит κ₁ элементов, то это означает, что множество имеет ту же мощность, что и континуум; это совершенно подобно тому, как множество содержащее 5 элементов, имеет ту же мощность, что и множество 1, 2, 3, 4, 5.

Рассуждениями, столь же элементарными, как и приведенные выше, Кантор показал, что совокупность точек, заполняющих квадрат или куб, имеет мощность континуума. Совокупность всех непрерывных функций одной или вообще определенного числа переменных имеет мощность континуума. Но совокупность всевозможных функций хотя бы даже одной переменной имеет уже более высокую мощность. В этом направлении можно идти сколь угодно далеко: наибольшей мощности не существует, — каково бы ни было множество, можно всегда составить множество, имеющее большую мощность.

Таково понятие о числе, созданное Кантором. Оно является выразителем мощности множества, носит количественный характер, но уходит далеко за пределы целого числа обыкновенной арифметики. Существенным и глубоким обобщением этой идеи является то обстоятельство, что числами выражается количество элементов не только в конечном, но и в бесконечном множестве.

29. Арифметика Кантора. Установив количественную точку зрения на число и расширив его далеко за пределы натурального ряда, Кантор строит арифметику этих чисел, основанную на их определении. Эта арифметика относится только к количественным числам (Kardinalzahlen), как их понимает Кантор, — к канторовым числам. Так как числа являются выражением мощности множества, то операциям над числами предпосылаются операции над самими множествами.

Пусть А и В будут два множества; составим новое множество С таким образом, чтобы оно содержало все элементы, входящие либо в множество А либо в множество В. Это множество мы будем называть суммой множеств А и В и будем писать С = А + В. Если множества А и В совершенно различны, т. е. не имеют вовсе общих элементов, то их сумма С содержит как все элементы одного множества, так и все элементы второго множества; если же множества А и В содержат и общие элементы, то множество С состоит из всех элементов множества А и тех элементов множества В, которых нет в А.

Пусть теперь а и b будут два каких-либо числа, А и В — два совершенно различных множества, мощности которых выражаются числами а и b в таком случае число с, выражающее мощность множества С = А + В, мы будем называть суммой чисел а и b: с = а + b. Этим устанавливается понятие о сумме любых двух количественных чисел. Легко понять, что сумма двух конечных чисел m и n в этом определении совпадает с суммой этих чисел, как ее определил Грассман; это может быть доказано методом совершенной индукции по отношению к любому из двух слагаемых. Но каковы бы ни были количественные числа, натуральные или трансфинитные, сумма их всегда обладает основными свойствами суммы натуральных чисел: законы переместительности и сочетательности остаются в силе. Это обусловливается тем, что законы эти остаются в силе для сумм самих множеств, т. е.

Обобщение того же определения Кантора на сумму нескольких слагаемых не представит затруднений.

Теперь обратим внимание на особенности, которые представляет сумма двух количественных чисел, когда хотя бы одно из них трансфинитное. Если мы возьмем исчислимое множество и к нему присоединим конечное число элементов, то, как мы видели выше, мы получим вновь исчислимое множество. Мощность первого множества есть κ, мощность второго есть n, мощность суммы вновь есть κ; следовательно, κ + n = κ. Прибавление конечного числа к трансфинитному дает вообще в сумме то же трансфинитное число. Более того, соединяя два исчислимых множества в одно, мы получаем исчислимое множество. Если, поэтому, множества А и В имеют мощности κ, то и А + В имеет ту же мощность; следовательно, κ + κ = κ.

Вследствие этих обстоятельств понятие о вычитании трансфинитных чисел уже не допускает однозначного определения, как действия, обратного сложению. Так, разность κ — κ может быть выражена любым натуральным числом и даже тем же числом κ.

Обращаясь теперь к умножению, определяем, прежде всего, произведение двух множеств. Положим, что множество А состоит из элементов А, А', А'',..., а множество В — из элементов В, В', В'',... Составим всевозможные пары вида (А, В), т. е. любой элемент первого множества соединим с любым элементом второго множества, и из всех этих пар как элементов составим множество. Это последнее множество мы будем называть В мы будем называть произведением множества А на множество В, так что В = А.В. Если С есть третье множество, состоящее из элементов С, С', С''..., то под произведением В = А.В.С разумеем множество, составленное из всевозможных сочетаний вида (А, В, С). Очень легко себе уяснить, что законы переместительности, сочетательности и распределительности остаются в силе.

Пусть теперь а, b, с будут три числа, A, B, C — множества, мощности коих этими числами выражаются; если B есть произведение множеств A.B.C, а р — число, выражающее его мощность, то число р называется произведением чисел а, b и с: р = а.b.с. Основные законы преобразования произведения остаются в силе, потому что они имеют место для произведения множеств.

Составим, согласно этому определению, произведение З.κ. За множество A, мощность которого выражается κ, примем натуральный ряд. В таком случае множество B будет:

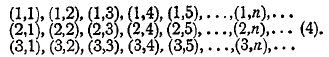
Это явно исчислимое множество, и потому З.κ = κ. Вообще n.κ = κ. Более того, если мы захотим составить произведение κ.κ, то должны будем составить такой же двойной ряд (в качестве множества B), продолжая его неограниченно не только вдоль каждой горизонтали, но и по вертикали. Это будет явно множество той же мощности, что множество (2) предыдущей главы, т. е. это есть исчислимое множество. Поэтому κ. κ = κ² = κ. Совершенно так же покажем, что κⁿ = κ^n-1.κ = κ, если n есть натуральное число. Но число κ^κ уже больше числа κ. Можно показать, что оно выражает мощность континуума, т. е., что κ^κ=κ₁.  В самом деле, чтобы составить множество B, имеющее мощность κ^κ, нужно составить κ исчислимых множеств, каждое мощности κ:

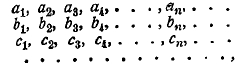
и из них составить множество, элементами которого будут служить комбинации

множество B будет состоять из всех элементов этого вида. Но ясно, что оно имеет ту же мощность, что и множество, составленное из всех дробей вида 0, αβγ..λ... , а это есть континуум.

Из того обстоятельства, что nκ = mκ, если m и n суть натуральные числа, следует, что установить понятие о делении, как об однозначном обращении умножения, здесь невозможно. Совокупность канторовых чисел не образует числового корпуса.

Изложенные выше основания канторовой арифметики количественных чисел могут произвести впечатление, что порядковое расположение их в этой теории роли не играет. Это, однако, не так. Для полной разработки этой теории Кантор не только был вынужден возвратиться к идее о порядковом характере всего числового ряда, но даже построить учение о так называемых «порядковых числах». Войти в подробности этого весьма важного учения здесь невозможно; ограничимся лишь указанием того, что приводит к этому учению и каков его важнейший результат.

Установив в предыдущей главе, при каких условиях мы считаем мощность одного множества большей, равной или меньшей, нежели мощность другого множества, мы не остановились на вопросе о том, можно, ли всегда утверждать, что из двух заданных множеств одно всегда имеет мощность, равную мощности другого, большую или меньшую ее. Иначе говоря, если даны два множества, которые не имеют одинаковой мощности, т. е. не могут быть приведены в однооднозначное соответствие, то всегда ли можно одно и только одно из этих двух множеств привести в однооднозначное соответствие с некоторой частью другого? Решение этого основного вопроса оказалось чрезвычайно трудным, и путь к нему лежит через учение о порядковых числах. Точкой отправления в этом учении служит расположение элементов множества, т. е. распределение их в такой порядок, при котором из любых двух его элементов один всегда бы предшествовал другому (а этот последний следовал бы за первым). Грассманова арифметика, как мы видели, имеет точкой отправления расположенный ряд — натуральный ряд; на этом всецело основан индуктивный метод построения арифметики. У Кантора такого ряда нет; ему необходимо создать более сложный ряд, который соответствовал бы более сложной структуре его количественных чисел. Кантор замечает, прежде всего, что самые элементы натурального ряда можно расположить чрезвычайно различно. Так, мы можем заменить натуральное расположение

1, 2, 3, 4, 5, 6, 7, 8,...,

в котором каждое нечетное число предшествует четному, расположением

2, 1, 4, 3, 6, 5, 8, 7,...,

в котором каждое четное число предшествует меньшему нечетному. В таком же роде возможно еще многообразно изменять последовательность членов натурального ряда. Но такого рода перераспределение, пример которого мы привели, Кантор не считает существенным. Гораздо более глубокое отличие от натурального ряда представляют собой расположения:

2, 3, 4, 5, 6, 7, 8,.. 1

или

3, 4, 5, 6, 7, 8....1, 2,

в которых один или два первых элемента перенесены в конец ряда. Еще большее отличие представляет расположение

1, 3, 5, 7, 9,... 2, 4, 6, 8, 10,...,

при котором каждое четное число следует за всеми нечетными.

При всем различии приведенных выше расположений членов натурального ряда, они все имеют одну существенную особенность, которая заключается в следующем: как бы мы в этих расположениях ни произвели сечение, каждая из двух частей имеет начальный элемент. Если, например, произвести в последнем расположении сечение, относя к первой группе все нечетные, а ко второй группе все четные числа, то первая группа будет иметь начальным элементом 1, а вторая — 2; если сечение произвести после 8, то вторая группа будет иметь первым элементом 10, и т. д. Такого рода последовательности Кантор называет строго расположенными, или вполне расположенными (wohlgeordnete Menge). Но если мы дадим членам натурального ряда расположение:

1, 3, 5, 7, 9, 11, ... 12, 10, 8, 6, 4,2,

в котором за всеми нечетными числами следуют все четные в обратном порядке, то это расположение не будет строгим; в самом деле, если мы здесь произведем сечение, отнеся к первой категории все нечетные, а ко второй — все четные числа, то вторая группа первого элемента не имеет: это нестрогое расположение чисел натурального ряда. Наиболее существенная особенность строго расположенных множеств заключается в следующем. Если два строго расположенных множества не имеют одинаковой мощности, то одно из них непременно имеет мощность некоторой начальной части другого. Таким образом, относительно строго расположенных множеств поставленный выше вопрос о сравнимости мощностей всегда решается в утвердительном смысле. Точнее: из двух множеств, элементы которых могут быть приведены в строго расположенные последовательности, одно всегда имеет либо ту же мощность, что и другое, либо большую, либо меньшую; здесь имеет место полная дизъюнкция. Чтобы поэтому установить, имеет ли также место такая дизъюнкция относительно двух любых множеств, нужно решить, можно ли элементы любого множества привести в строго расположенную последовательность. Это и был коренной вопрос во всей канторовой арифметике. Вопрос этот представлял весьма большие трудности, так что Гильберт в своей речи на Парижском всемирном конгрессе математиков отнес его к числу труднейших задач, стоящих перед математическим миром. Цермелло дал его решение: рядом весьма тонких рассуждений он показал, что строгое расположение элементов любого множества всегда может быть достигнуто. С тех пор учение о множествах получило чрезвычайно широкое развитие, и идеи Кантора стали краеугольным камнем современной теории функций действительного переменного (см. функция). Нужно, однако, сказать, что доказательство Цермелло нельзя считать общепризнанным.

30. Корпус трансфинитных чисел и неархимедова геометрия. Арифметика Кантора, как мы видели выше, не дает места обратным операциям — вычитанию и делению. Вследствие этого построенная Кантором система трансфинитных чисел не представляет собою числового корпуса. Кантор только продолжил натуральный ряд, и все его дальнейшие числа тоже носят характер целых чисел. Гильберт подошел к идее трансфинитных чисел с другой стороны и создал настоящий корпус трансфинитных чисел. Если Кантор продолжил ряд натуральных чисел, то Гильберт продолжил в обе стороны за бесконечность весь комплекс действительных чисел. Комплекс не сохранил при этом непрерывности, но зато стал числовым корпусом. Составим множество следующим образом. Введем в его состав, прежде всего, все целые и дробные алгебраические функции одного действительного переменного с действительными коэффициентами. Каждая такая функция будет, следовательно, иметь вид

Сюда же войдут, в частности, функции, сводящиеся к постоянным, вида

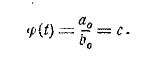
Вслед за этим мы введем в состав нашего множества функции, которые получаются путем производства над любым конечным числом ранее введенных функций φ₁(t), φ₂(t),…,  φ_n(t)  операции

Получив, таким образом, функции, содержащие один квадратный радикал, мы составим новые функции, которые получаются путем производства над всеми введенными уже функциями рациональных операций и извлечения корня квадратного из суммы квадратов. Далее, мы приобщим все возможные функции, которые тем же путем получаются из предыдущих функций, и т. д. Мы можем, таким образом, сказать, что в состав нашего множества войдут все функции, которые получаются из целых алгебраических функций с действительными коэффициентами путем последовательного производства четырех рациональных операций и извлечения корня квадратного из суммы квадратов.

Теперь, прежде всего, ясно, что, если наше множество содержит функции ω₁(t)  и ω₂(t),   то оно будет содержать также функции

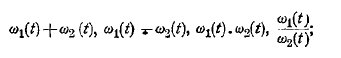
последнюю в том предположении, что ω₂(t) не сводится тождественно к нулю. Это множество функций образует, таким образом, числовой корпус. Построенное этим путем множество Гильберт претворяет в величину. Для этого ему нужно установить соглашения, при которых он будет считать один из элементов этого множества равным другому, большим или меньшим его. Он пользуется для этого тем обстоятельством, что его функции алгебраические — рациональные или иррациональные, а потому каждая из них может обратиться в нуль лишь конечное число раз. Следовательно, при достаточно больших значениях независимого переменного t функция сохраняет уже определенный знак; точнее, для каждой функции нашего множества ω(t), не сводящейся тождественно к нулю, существует такое положительное число Т, что при t > Т функция всегда имеет один и тот же знак. Если этот знак есть +, то мы будем говорить, что ω(t) становится на бесконечности положительной; если этот знак есть —, то мы будем говорить, что функция становится на бесконечности отрицательной.

Пусть теперь ω₁(t) и ω₂(t) будут два элемента нашего множества. Будем говорить, что ω₁(t) = ω₂(t), если разность ω₁(t) — ω₂(t) тождественно равна нулю; будем говорить, что ω₁(t) > ω₂(t), если разность ω₁(t) — ω₂(t) становится на бесконечности положительной, и будем говорить, что ω₁(t) < ω₂(t), если та же разность становится на бесконечности отрицательной. Что все постулаты сравнения при этих критериях соблюдены, это никто не затруднится обнаружить.

Множество претворено, таким образом, в величину. Элементы этого множества Гильберт рассматривает как своеобразные числа; мы будем их называть гильбертовыми числами. В состав их входят и все обыкновенные действительные числа, так как они были введены в этот комплекс. Но, если мы возьмем, например, число, выражаемое функцией τ, и число с, выражаемое обыкновенным действительным числом, то разность τ — с становится на бесконечности положительной, каково бы ни было число с. Поэтому гильбертово число τ больше всякого обыкновенного числа с; это есть число трансфинитное. Совокупность гильбертовых чисел представляет собою числовой трансфинитный корпус. Причина парадоксального, на первый взгляд, обстоятельства, что мы оперируем над бесконечными числами, здесь коренится в том определении, которое мы приняли в качестве критерия сравнения чисел; при этой конвенции здесь нет ничего трансцендентального.

Располагая корпусом трансфинитных чисел, мы можем построить и трансфинитную геометрию. С этой целью построим аналитическое пространство (см. гл. 18, ст. 408'/10'), в котором точкой будут служить значения трех независимых переменных (х, у, z), произвольно выбранные из всей совокупности гильбертовых чисел. В остальном геометрия строится, как аналитическая геометрия Евклида. За расстояние между двумя точками (х₁, у₁, z₁) и (х₂, у₂, z₂) принимается число (вообще говоря, трансфинитное)

за прямую принимается совокупность точек, координаты которых удовлетворяют двум независимым линейным уравнениям, и т. д. Если мы на оси абсцисс возьмем точки (0, 0, 0), (1, 0, 0), (2, 0, 0), (3, 0, 0), …, (n, 0, 0), то расстояния между двумя последовательными точками равны 1. Расстояние точки (n, 0, 0) от начала координат равно n. Между тем расстояние точки (τ, 0, 0), также лежащей на оси абсцисс, от начала координат равно τ и, следовательно, больше любого расстояния n, выражающегося обыкновенным положительным числом. Откладывая по оси абсцисс от начала координат последовательно равные отрезки, имеющие единицу длины, мы никогда не достигнем единицу длины, мы никогда не достигнем точки (τ, 0, 0), лежащей на той же оси. Принцип Архимеда, таким образом, в этой геометрии не имеет места. Гильберт и построил эту геометрию, чтобы обнаружить возможность неархимедовой геометрии и, следовательно, независимость постулата Архимеда. Великий эллинский геометр был прав, когда внес это положение в число не доказываемых принципов геометрии. Так арифметика и геометрия помогают друг другу в разрешении этих трудных вопросов.

31. Математика и логика. В предыдущих главах изложен ход эволюции учения о теоретических основах математики. В своем современном виде учение это, как мы старались его осветить, основано на следующих принципах.

Математика, как научная система, в конечном своем построении, во всех своих разветвлениях представляет собой формальную науку, строго логически развивающуюся из основных положений — определений и постулатов. Эти определения представляют собой чистые соглашения, присваивающие определенным символам (терминам, понятиям) те или иные, нами устанавливаемые, значения. К определениям присоединяются постулаты, отличающие категории объектов, которые мы желаем изучать, от других категорий, также удовлетворяющих определениям, но оставляемых нами в стороне.

В выборе наиболее целесообразных определений и постулатов, т. е. таких, которые приведут к формальной системе, способной целесообразно выражать соотношения между объектами внешнего мира, нами руководит опыт; в этом — эмпирический источник математического познания. Но соглашения все же остаются конвенциями; поэтому характер математического познания конвенциональный.

Все исходные положения каждой математической дисциплины должны быть совместны, т. е. не должны заключать внутреннего противоречия. Они должны быть независимы, т. е. ни одно из них не должно быть следствием остальных. Из этих положений путем строгой логической дедукции разматывается весь математический материал. Определения, как мы указывали в своем месте, должны сводить математические понятия к другим основным понятиям, лежащим за пределами математики.

Из всего этого видно, какая сложная задача возлагается на логику. Она должна установить отсутствие противоречий в принятой системе основных положений; она должна руководить каждым шагом в процессе умозаключения; она должна снабдить математику теми общими понятиями, к которым основные определения сводят математические понятия (см. математика).

К этому присоединяется еще один, и притом основной, вопрос. При доказательстве совместности и независимости исходных положений геометрии, как мы видели (гл. 18), опорной базой служит арифметика. Для самой арифметики этой базой должна служить логика. Спрашивается, стоит ли логика на высоте этих заданий? Как известно, дедуктивная логика, построенная Аристотелем, глубокого усовершенствования до XIX в. не получила. В состоянии ли она справиться с трудной задачей, на нее возлагаемой учением о теоретических основаниях математики?

Фреге, по-видимому, первый решительно ответил отрицательно на этот вопрос. Конечно, как всегда, Фреге имел своих предшественников. Его идеи можно найти у Лейбница, у Бернулли; они получили уже значительное развитие в замечательном сочинении Буля «Исследование о законах мышления». Но твердым и решительным новатором явился Фреге. За ним последовала итальянская школа: Пеано, Падуа, Вайлати, Бурала-Форти и Пиери, наконец, германская — Шредер, Штольц и английская — Уайтхед и Рессель.

По воззрениям этих ученых, логический вывод, как мы его производим, прежде всего, не дает гарантий безупречности потому, что он осуществляется словами, содержащими уже привходящие идеи. В этом обилии слов тонет строго логический вывод, как геометрический вывод тонет в интуиции, привносимой чертежом. Чтобы устранить этот коренной дефект, надо там, где вывод должен быть совершенным, оградить самый язык от злоупотребления понятиями, в основные положения не входящими. Для этой цели Фреге, а за ним итальянская школа — вводят своеобразный язык и начертания, существенно отличающиеся от наших. «Идеография» Фреге и Пеано создает символы, выражающие письменно не звуки (как наши буквы), а понятия — идеи. В цепи заключений вследствие этого фигурируют только те понятия, которые получили символическое выражение; этим устраняется привнесение чуждых понятий. Далее, надо установить алгорифм, по которому из суждений, в этом своеобразном символическом начертании выраженных, можно было бы делать логические выводы. Анализ этой задачи обнаружил, что основы логики для этой цели должны быть значительно углублены. Логике суждений должны быть предпосланы логика классов и логика отношений. Эти учения, в свою очередь, оказались далеко не простыми и в своем развитии потребовали методов, очень близких математическому алгорифму. Математика, таким образом, срослась с логикой в одно целое, и самая система логики в последние десятилетия стала предметом исследования математиков. Здесь развернулись вопросы большой трудности. По воззрениям школы математической логики, строгая аксиоматика невозможна ни в какой дисциплине без аксиоматики самой логики. Во главе этого направления стоит в настоящее время выдающийся математик Давид Гильберт.

Нужно, однако, сказать, что это направление имеет и своих решительных противников. К числу их принадлежал А. Пуанкаре. При всей своей склонности к конвенционализму, он считал, что «логистики» слишком отвлекают математическую мысль в чуждую область, — что созданный ими алгорифм требует огромного труда для усвоения, и он не видел гарантии в том, что в этих сложных построениях нет новых погрешностей, новых трудностей. Эту точку зрения настойчиво поддерживал в Германии Стюди. В последнее время выдвинуто также возражение, что все вообще миросозерцание Гильберта является идеалистическим. Однако, не решая здесь вопроса о том, каково общее мировоззрение Гильберта, можно с уверенностью утверждать, что построенное им учение об аксиоматике арифметики и логики ничего общего с идеализмом не имеет. Сомнения и трудности, стоящие на этом пути, лежат в другой плоскости. Логики утверждают, что они создали целый новый мир математических построений, что им принадлежит будущее. Гильберт находит, что вне обоснования логики невозможна никакая аксиоматика. Их противники, люди самого различного миросозерцания, утверждают, что нельзя строить логики, опираясь на самое логику. И это тем серьезнее, что с разных же точек зрения подвергнуты сомнению основные формы классической логики (Шатуновский, Брауэр).

32. Итак, в конечном своем построении, вернее, в стадии известного завершения каждого отдела, математика представляет собою формальную систему. С наибольшей определенностью это относится к тем математическим дисциплинам, которые сложились в особенно устойчивые формы, как арифметика, элементарная геометрия и т. п. Но как осуществляется самое математическое творчество? Какими путями идет эволюция математических наук и математических идей? На том, что в этой стадии, в процессе творчества, математические дисциплины развертываются формально, на этом не стоит никто. Каковы же иные пути и методы, которыми осуществляется в математике научное творчество? Кант и его школа стоят на той точке зрения, что здесь руководящую роль играет «внутреннее воззрение» (Anschauung); школа Милля и здесь видит руководящее начало только в чистом эмпиризме; Пуанкаре приписывает эту роль «интуиции». С подъемом марксистского миросозерцания в СССР выдвигаются на первый план диалектические методы.

Вряд ли может подлежать сомнению, что диалектическая логика играет коренную роль и в процессе математического творчества. Но четкое установление этой роли, выяснение ее соотношения с формальной логикой — это еще задача большой трудности. Наиболее распространенное воззрение на размежевание формальных и диалектических методов в математическом творчестве заключается в том, что формальные методы преобладают в отдельных предложениях, а диалектические — в процессе конструирования математической дисциплины, как целого. Но и доказательство каждого более или менее значительного предложения часто имеет сложное строение, разбивается на значительные части; и в отношении каждого предложения возникают те же вопросы, что и по отношению к целому. Установить здесь границы, отделяющие одни логические приемы от других, тем более трудно, что все эти различные приемы в процессе активной творческой мысли постоянно переплетаются. В этом вопросе мы стоим еще перед задачей текущего дня, которая ждет своего разрешения.

Литература. 1. Общая. Н. Weber и. J. Wellstein, «Enzyklopadie der Elementar mathematik», I—III, Leipz., 1903—07, 3 изд. — 1915 (есть русский перевод двух томов — Г. Вебер и И. Вельштейн, «Энциклопедия элементарной математики»: I — «Арифметика и алгебра», Одесса, 1907; II — «Основания геометрии», Одесса, 1910; первая часть I т. переиздана в 1927 г., М.); F. Klein, «Elementar mathematik vom höheren Standpunkt aus», литографированное издание, 1908—09, 3-е, посмертное издание — 3 т., 1924—26 (первая часть переведена на русский язык — «Вопросы элементарной и высшей математики», Одесса, 1912); Р. Enriques, «Questioni  riguardanti la geometria elementare», 1900 (русский перевод — «Вопросы элементарной геометрии», СПБ., 1913); H. Poincaré, «Science et hypothèse» 1903 (русский перевод — «Наука и гипотеза», М., 1904); Н. Poincaré, «Science et methode» (русский перевод — «Наука и метод»); F. Enriques, «Les concepts fondamentaux de la science», Р., 1919; L. Couturat, «Les principes des mathématiques», Р., 1905 (русский перевод П. С. Юшкевича — «Философские принципы математики», СПБ, 1913); Н. Weyl, «Die heutige Erkentnisstheorie in der Mathematik», Erlangen. 1926; Н. Weyl, «Philosophiе der Mathematik und Naturwissenschaften» München u. Berlin, 1926; Baldus, «Vorlesungen über die Entwickelung der Mathematik»; Р. Klein, «Vorlesungen über die Entwickelung der Mathematik im XIX Jahrhundert», Berl., I—1926, II—1927; Hölder «Mathematische Methode», Berl., 1927; Os. Becker «Mathematische Existenz», Leipz., 1925. — II. Основания арифметики. Н. Grassmann, «Lehrbuch der Arithmetik» Berl., 1861; R. Dedekind, «Was sind und was sollen die Zahlen», Braunschweig, 1888; R. Dedekind, «Stetigkeit und irrationale Zahlen», Braunschweig, 1872 (русский перевод — «Непрерывность и иррациональные числа», Одесса, под редакцией С. О. Шатуновского, 4 изд., 1923); О. Stole, «Vorlesungen über allgemeine Arithmetik», Leipz., 1885; С. Färber, «Arithmetik», Leipz., 1911 (есть русский перевод); М. С. Волков, «Эволюция понятия о числе» 1899; Hölder, «Die Arithmetik in strengen Begründung», Leipz., 1914; Е. Husserl, «Philosophie der Mathematik», Halle, 1891; В. Russel, «Introduction to mathematical philosophy», 1919 (есть немецкий перевод — «Einführung in die mathematische Philosophie», Berl., 1923).   III. Основания геометрии. В. Ф. Каган, «Основания геометрии», ч. I — Одесса, 1905, ч. II — Одесса, 1907 (содержит историко-литературные указания); W. Killing, «Еіnführung in die Grundlagen der Geometrie» 2 т., Paderborn, 1893—98; В.  Russel, «Foundations of geometry» (есть французский перевод); С. А. Богомолов, «Основания геометрии», М., 1923; Р. Klein, «Vеrgleichende Betrachtungen über neuere geometrische Forschungen», Erlangen, 1872; В. Ф. Каган, «Очерк геометрической системы Лобачевского», Одесса, 1900; Н. Liebman, «Nichteuklidische Geometrie», Leipz., 1905; F. Schar, «Die Grundlagen der Geometrie», Leipz., 1909; Бонола, «Неевклидова геометрия» (перевод с итальянского, СПБ., 1910): J. Coolidge, «The elements of noneuclidean geometry», Oxford, 1909; М. Simon, «Nichteuklidische Geometrie» Leipz., 1926; Р. Klein, «Nichteuklidische Geometrie» 1927 (первое издание было в литографированном виде); D. Hilbert, «Die Grundlagen der Geometries 1899 (4 изд. — 1913; русский пер. А. В. Васильева — «Основания геометрии», П., 1923); L. Eisenhart, «Riemannian Geometry», Princeton, 1926; L. Eisenhart. «Nonriemannian Geometry», Princeton, 1927. IV. Учение о множествах. В. Bolzano, «Paradoxien des Unendlichen», 1851 (2 изд. — 1890; русский перевод — «Парадоксы бесконечного», Одесса, 1911); А. Fraenkel, «Einleitung in die Mengenlehre» 2-е Aufl., Berl., 1923; F. Hausdorff, «Grundzüge der Mengenlehre», Leipz., 1914; Н. Weyl, «Das Kontinuum», 1918. V. Математика и логика. G. Frege, «Grundlagen der Arithmetik», Breslau, 1884; В. Russel (вместе с А. Whitehead), «Principia Mathematics», I—III, 1910; D. Hilbert, «Neubegründung der Mathematik», Hamburg, 1922; Н. Weyl, «Ueber die neue Grundlagenkrise der Mathemati», Mathem. Zeitschrift, 1921.

В. Каган.