Теория чисел

Теория чисел. Под этим именем обычно разумеют, в первую очередь, учение о свойствах обыкновенных целых чисел; но в более широком понимании теория чисел обнимает собой и другие числовые образования.

Теория  чисел представляет собой одну из самых древних и наиболее разработанных ветвей математики; тем не менее, по обилию насущных и актуальных проблем она и в настоящее время в ряду математических дисциплин занимает одно из первых мест, привлекая к себе усилия значительнейших научных авторитетов.

Так как из четырех основных арифметических действий только одно деление не всегда выполнимо в области целых чисел, то, естественно, первые и основные проблемы теории чисел связываются с вопросами делимости чисел и разложения на множители («мультипликативная» теория чисел). Основную роль здесь играет понятие абсолютно простого или, коротко, простого числа; так называется положительное число, отличное от единицы и не имеющее иных делителей, кроме единицы и самого себя (например, 2, 3, 5, 7, 11 и т. д.); фундаментальное значение этих чисел для мультипликативной теории обусловливается тем, что из них, как элементов, посредством умножения строятся все другие числа; в самом деле, имеет место основное предложение, в силу которого всякое положительное число, кроме единицы, может быть представлено как произведение простых сомножителей; при этом, что особенно важно, такое представление возможно единственным образом (если отвлечься от порядка сомножителей). Науку уже давно занимал вопрос о том, как расположены простые числа в ряду всех целых положительных чисел; здесь никак не удавалось уловить сколько-нибудь простых законов. И хотя в настоящее время многое в этом направлении уже известно, тем не менее, далеко не все относящиеся сюда вопросы получили разрешение. Еще Эвклид установил существование бесконечного множества простых чисел. Но сверх этого почти ничего не было известно вплоть до середины XIX столетия, когда работами Чебышева и Riemann’а проблема была, наконец, сдвинута с мертвой точки

Вопрос шел, в первую очередь, о «густоте» расположения простых чисел; обозначая через π(n) число простых чисел, не превосходящих n, естественно было спрашивать о характере роста этой величины π(n)  при безграничном возрастании числа n. Euler’у было известно, что дробь π(n)/n стремится к нулю при безграничном возрастании числа n; это можно истолковать так, что простых чисел имеется бесконечно мало в сравнении со множеством всех целых положительных чисел.

Но, понятно, этот результат еще очень мало говорит. Наука настойчиво стремилась к тому, чтобы найти простое аналитическое выражение, которое могло бы приближенно выражать собой эту сложную арифметическую функцию π(n). Элементарные подсчеты показывали, что выражение  n/lgn на первых порах дает хорошее приближение; но прошло много времени, прежде чем в этом направлении удалось установить что-либо непреложное. Чебышев показал, что отношение

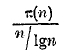
остается, при безграничном возрастании и, заключенным между двумя положительными числами. Целью дальнейших стремлений было установить, что это отношение с возрастанием n безгранично приближается к единице. Это удалось доказать лишь в 1896 г. сложными методами анализа, предначертанными Riemann’ом в его известной работе, опубликованной в середине прошлого столетия. В дальнейшем требовалось возможно точнее оценить порядок роста разности

т. е. той погрешности, какую мы делаем, заменяя функцию π(n)  ее приближенным выражением. Эта задача и по настоящее время далека от полного разрешения.

Другой интересный круг проблем, связанных с простыми числами, был порожден известной задачею об арифметической прогрессии. Уже в XVIII столетии был высказан (основанный на неточных рассуждениях) взгляд, что всякая арифметическая прогрессия, разность которой не имеет общих делителей с первым членом, должна содержать бесконечное множество простых чисел.

Однако, доказать этого долгое время не удавалось, и только в середине XIX в. Lejenne Dirichlet впервые точно обосновал эту теорему, базируясь на методах анализа. После этого возник ряд аналогичных проблем о существовании бесконечного множества простых чисел той или иной наперед заданной формы. По большей части задачи этого рода сопряжены с весьма значительными трудностями и остаются до настоящего времени неразрешенными.

Для современной теории чисел вообще является чрезвычайно характерным пользование принципиально инородными ей методами анализа, т. е. учения о непрерывно изменяющихся величинах. Собственно арифметических методов эта наука, в сущности, почти не знает, несмотря на свою глубокую древность. Как всякая математическая дисциплина, теория чисел выросла из отдельных частных задач, среди которых с древности первое место занимал так называемый неопределенный анализ, т. е. решение уравнений в целых числах. Математики древнего мира и эпохи Возрождения, а также и начала нового времени, много занимались такого рода задачами, не пытаясь объединить их в целое единым методом.

Сколько-нибудь общие исследования в этом направлении начались со времени Euler’а и Legendre’а; но лишь Gauss’у удалось дать сводку имевшихся результатов (с присоединением многих новых) в виде единой системы в его знаменитых «Disqnisitiones Arithmeticae». Им же был создан единственный элементарный арифметический метод — так называемая теория сравнений, являющаяся в значительной степени просто техническим приемом.

Принцип этой теории состоит в том, что два числа а и b, дающие при делении на некоторое число m один и тот же остаток, обладают по отношению к этому числу рядом общих свойств (например, имеют с этим числом m одинаковых общих делителей), и потому во многих вопросах могут заменять друг друга. Эту взаимную связь чисел а и b Gauss называет сравнимостью по модулю m; число m называется модулем сравнения, а записывается этот факт так:

Соотношение сравнимости обладает многими свойствами простого равенства, и именно в этом — главная сила и продуктивность нового понятия, введенного Gauss'oм. Эта аналогия простирается особенно далеко в том случае, когда модуль m есть число простое, вследствие чего теория таких сравнений особенно хорошо разработана. Сравнения могут содержать неизвестные, и тогда встает вопрос об их решении, аналогично алгебраическим уравнениям. В частности, проблемы, связанные с решением сравнений второй степени с одним неизвестным, приводят к обнаружению весьма интересных закономерностей, сведенных Gauss’ом в цельную теорию.

Учение о сравнениях явилось мощным вспомогательным орудием теории чисел. Оно позволило во многих случаях значительно упростить рассуждения и благодаря этому сделать прозрачными скрытые до тех пор закономерности. В руках самого Gauss’а это учение дало, прежде всего, систематизацию неопределенного анализа второй степени. До этого систематически разработаны были только законы решения в целых числах уравнений первой степени. Предшественники Gauss’а, хотя и много занимались уравнениями второй степени, все же всегда вынуждены были ограничиваться более или менее частными случаями. Только на основе теории сравнений Gauss’у удалось рассмотреть вопрос в его общем виде и дать вполне законченные результаты для случая двух неизвестных. Задача приводится к решению в целых числах уравнений вида

ax² + bxy + cy² = m, (1)

где x и у — неизвестные. Левая часть этого уравнения, при переменных x и у, представляет собою бинарную квадратичную форму; поставленная задача сводится, таким образом, к вопросу о представлении данного числа m с помощью данной квадратичной формы.

Это естественно приводит к необходимости построения арифметической теории квадратичных форм — теории, которая является одним из лучших созданий арифметики и до настоящего времени привлекает к себе внимание исследователей. Значительный интерес представляют собой и различные обобщения этой теории, получающиеся либо путем увеличения числа переменных, либо повышением степени формы. Здесь область исследований становится уже значительно труднее. Чрезвычайно важный общий результат был получен в XX столетии норвежским математиком Thue: оказалось, что, в то время как уравнение (1), вообще говоря, может иметь бесчисленное множество решений, уравнение того же типа, где только в левой части стоит (бинарная) форма степени выше второй, всегда (за исключением нескольких тривиальных случаев) имеет не более конечного числа решений.

Одну из самых трудных областей теории чисел составляют так называемые аддитивные проблемы, т. е. вопросы, связанные с представлением числа в виде суммы слагаемых того или иного заранее заданного вида. Сюда относятся большая часть знаменитых задач теории чисел, отчасти не решенных и до настоящего времени. Перечислим важнейшие из этих задач.

Уже Lagrange’eм было доказано, что всякое положительное число может быть представлено в виде суммы четырех квадратов (трех квадратов еще недостаточно, как показывает пример числа 7 = 2² + 1² + 1² + 1²). Позднее удалось установить, что каждое число может быть представлено в виде суммы девяти кубов. Естественно, возник вопрос: можно ли для любого показателя k найти такое число s, что всякое число может быть представлено в виде суммы s k-ых степеней? (s=4 при k=2, s=9 при k=3). Это — знаменитая задача Waring’а. Она была впервые решена в положительном смысле Hilbert’ом в 1907 г. Второе, гораздо более прозрачное доказательство било дано в 1918 г. Hardy и Littlewood’oм; наконец, наиболее простое доказательство той же теоремы было опубликовано в 1925 г. Виноградовым.

Особенно замечателен метод, созданный английскими математиками Hardy и Littlewood’oм. Этот метод, основанный на теории функций комплексного переменного, распространяется с большим успехом и на ряд других проблем аддитивной теории чисел и, несомненно, представляет собой одно из лучших достижений арифметики за последние десятилетия. В частности, с помощью этого метода впервые удалось найти подход к известной проблеме Goldbach’а: доказать, что всякое четное число, кроме 2, может быть представлено как сумма двух абсолютно простых чисел. Эта задача, поставленная почти 200 лет тому назад, не только остается до сих пор неразрешенной, но до создания нового метода мы не знали к ней ни одного серьезного подхода; правда, и сейчас еще проблема не решена; однако, метод Hardy и Littlewood’а позволяет весьма глубоко проникнуть в сущность тех трудностей, какие лежат на пути ее разрешения, и тем самым впервые подает нам надежду с течением времени разобраться в этих трудностях.

Наконец, в ряду классических проблем аддитивной теории чисел необходимо упомянуть о так называемой Великой теореме Fermat Состоит она в том, что уравнение

xⁿ + yⁿ = zⁿ

при любом данном n > 2 не может быть решено в целых положительных числах. Fermat утверждал почти 300 лет тому назад, что ему удалось доказать это предложение; однако, этого доказательства не сохранилось, и, несмотря на усилие ряда крупнейших ученых, вопрос остается до настоящего времени открытым. В многочисленных работах, посвященных этому вопросу, удалось доказать справедливость утверждения Fermat для целого ряда отдельных значений n; но в общем виде трудность проблемы столь велика, что не поддается разрешению никакими известными нам приемами.

Говоря о распределении простых чисел, мы уже встречались с арифметической функцией π(n). Исследование законов роста арифметических функций (т. е. функций, определяемых арифметическим путем) составляет одну из важнейших задач теории чисел. Обычно вопрос ставится так, что ищется возможно простая аналитическая функция, закон роста которой возможно точнее воспроизводил бы поведение данной арифметической функции при больших значениях n. Если ψ(n) — данная арифметическая функция, а χ(n) — та аналитическая функция, которая должна приближенно выражать ее, то наиболее обычным является требование, чтобы отношение

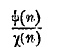
стремилось к единице при безграничном возрастании числа n; если это требование выполнено, функции ψ(n) и χ(n) называют взаимно эквивалентными или асимптотическими.

Так, функции π(n) и n/lgn взаимно эквивалентны. Но большинство арифметических функций имеет столь сложное поведение, что его не удается имитировать с помощью простых аналитических выражений. Так, функция τ(n), выражающая число различных делителей числа n, имеет, очевидно, весьма сложный характер; для всякого абсолютно простого n τ(n) = 2, в то время как для надлежаще подобранных значений n τ(n) может, очевидно, получать сколь угодно большие значения. Здесь не может идти речь об отыскании асимптотической функции. Однако, среднее значение

также представляющее собой некоторую арифметическую функцию, имеет уже гораздо более правильный характер роста, благодаря взаимному сглаживанию больших и малых значений функции   τ(n); оно имеет простую асимптотическую функцию Ign. Аналогичные явления мы имеем и во многих других случаях, вследствие чего приходится иметь дело, главным образом, с изучением средних значений арифметических функций. Помимо отыскания асимптотической функции, здесь уделяется много внимания и второй проблеме — оценке погрешности, получаемой при замене данной арифметической функции ее приближенным выражением. Именно этого рода вопросам посвящена большая часть современной литературы об арифметических функциях.

Помимо обыкновенных целых чисел, о которых была речь до сих пор, теория чисел имеет дело в первую очередь с так называемыми алгебраическими целыми числами. Алгебраическим числом называется всякий корень алгебраического уравнения с целыми коэффициентами.

Алгебраическое число называется целым, если определяющее его уравнение может быть выбрано так, чтобы коэффициент при его старшем члене был единицей. В отличие от алгебраических целых чисел обычные целые числа называют целыми рациональными.

Если дано какое-либо алгебраическое число, то всякая рациональная функция этого числа с рациональными коэффициентами также есть алгебраическое число. Совокупность всех таких рациональных функций данного числа называется алгебраической областью, определяемой этим числом. Каждая алгебраическая область содержит бесчисленное множество целых чисел и, между прочим, — все целые рациональные числа. Целые алгебраические числа, входящие в состав какой-либо области, по своим взаимоотношениям во многом напоминают обычные (рациональные) целые числа. Сумма, разность и произведение двух целых чисел давкой области в свою очередь являются целыми числами той же области. При делении же (если только делитель не нуль) мы всегда получаем число той же области, но не обязательно целое. Это дает повод рассматривать и здесь вопросы делимости. Подобно рациональной области, во всякой алгебраической области определяются абсолютно простые числа, и легко доказывается, что всякое целое число области может быть представлено, как произведение абсолютно простых чисел. Однако — и этим обусловливается главный интерес дела — такое разложение на простые множители в алгебраических областях, вообще говоря, не оказывается единственным. Этот факт, открытый Kummer’ом в его исследованиях о Великой теореме Fermat, делает теорию делимости в алгебраических областях сложной и многообразной и обусловливает собой ее особую прелесть. Оказывается, что однозначность разложения может быть восстановлена ценой введения фиктивных, так называемых идеальных чисел, что делает всю теорию стройной и легко обозримой. Последователи Kummer’а позднее заменили его «идеальные» числа вполне реальными образованиями (так называемыми «идеалами»), представляющими собой определенные множества целых чисел данной области.

В настоящее время теория алгебраических областей представляет собой широко разработанную, весьма содержательную ветвь арифметики, проблемы которой до сих пор служат предметом многочисленных исследований. Благодаря тому, что и здесь имеется теория делимости, все проблемы мультипликативной теории обычных чисел могут быть с соответствующими изменениями перенесены на алгебраические области. Арифметическая теория алгебраических областей не только представляет значительный самостоятельный интерес, но вместе с тем способствует и развитию арифметики обычных чисел. Так, важнейшие результаты, полученные в области проблемы  Fermat, основываются на теории алгебраических чисел; на этой же теории основано и доказательство упомянутой выше теоремы Thue о неопределенных уравнениях.

Всякое не алгебраическое число называется трансцендентным. Арифметические исследования, связанные с трансцендентными числами, принадлежат к числу труднейших в теории чисел. Сюда, прежде всего, относятся исследования арифметической природы классических постоянных. Уже давно было известно, что числа е и π — иррациональны; однако, представило чрезвычайные трудности доказать, что оба эти числа трансцендентны — результат, имеющий фундаментальное значение для анализа и геометрии. Для многих других важных постоянных математического анализа (например, для Euler’овой константы G) до настоящего времени не решен даже возрос об их рациональности иди иррациональности.

Уже Liouville’ем было замечено, что алгебраические числа, при их приближенном выражении посредством рациональных дробей, подчиняются некоторым особым законам. Это дало возможность построить первые примеры трансцендентных чисел («числа Liouville’я»); это же в свое время послужило поводом к широкому и систематическому изучению законов приближенного выражения иррациональных чисел посредством рациональных дробей — законов, в которых с особой яркостью сказывается арифметическая природа каждой иррациональности. Это учение при дальнейшем своем расширении переходит в теорию приближенного решения уравнений в целых числах (так называемые «диофантовы приближения») — одну из интереснейших глав современной арифметики, систематическая разработка которой была начата Минковским. Теория диофантовых приближений в настоящее время оказывает существенную помощь теории чисел в ее дальнейшем развитии. Характерной методологической чертой этой ветви арифметики являются применяемые в ней по почину Минковского геометрические методы, действительно приносящие здесь очень хорошие результаты («Геометрия чисел»).

Литература. Элементы: Д. Ф. Егоров, «Элементы теории чисел»; более полный курс: Lefeane- Dirichlet, «Vorlesungen über Zahientheorie», 4 Aufl.; фундаментальный курс: Landan, «Vorlesungen über Zahlentheorie», 1927 (это же трехтомное руководство можно рекомендовать и по вопросам аддитивной теории и по теории алгебраических чисел). Специально по распределению простых чисел: Landau, «Handbuch der Lehre von der Vertcilung der Primzahlen», 1909 (2 тома). Специально по арифметическому анализу иррациональностей: Bachmann, «Vorlesungen über die Natur der Irrationalzahlen»; Minkowski, «Diophantische Approximationen».

А. Хинчин.